Chapter 6, Problem 6.90P

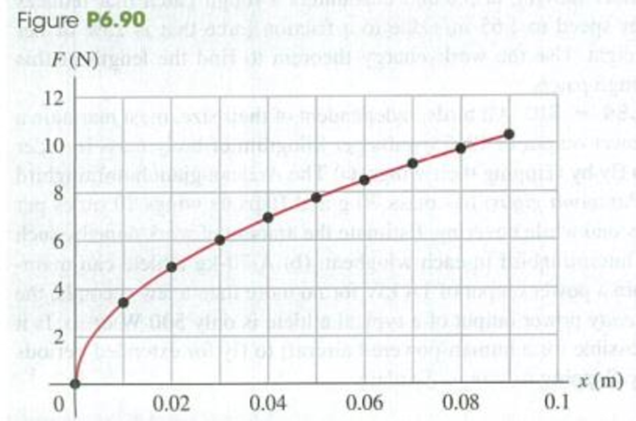
DATA Figure P6.90 shows the results of measuring the force F exerted on both ends of a rubber band to stretch it a distance x from its unstretched position. (Source: www.scicnccboddics.org) The data points are well fit by the equation F = 33.55x^0.4871, where F is in newtons and x is in meters, (a) Does this rubber band obey Hooke’s law over the range of x shown in the graph? Explain, (b) The stiffness of a spring that obeys Hooke’s law is measured by the value of its force constant k. where k = F/x. This can be written as k = dF/dx to emphasize the quantities that are changing. Define k_eff = dF/dx and calculate k_eff as a function of x for this rubber band. For a spring that obeys Hooke’s law, k_eff is constant, independent of x. Does the stiffness of this band, as measured by k_eff, increase or decrease as x is increased, within the range of the data? (c) How much work must be done to stretch the rubber band from x = 0 to x = 0.0400 m? From x = 0.0400 m to x = 0.0800 m? (d) One end of the rubber band is attached to a stationary vertical rod, and the band is stretched horizontally 0.0800 m from its unstretched length. A 0.300-kg object on a horizontal, friction less surface is attached to the free end of the rubber band and released from rest. What is the speed of the object after it has traveled 0.0400 m?