
(a)
The force vs. reduction in height curve in open die forging of cylinder for
(a)
Explanation of Solution
Given:
The initial thickness of the specimen is
The initial diameter of the specimen is
The friction coefficient is
The velocity of the hydraulic press is
Formula used:
The expression for the flow stress is given as,
Here,
The expression for the true strain is given as,
Here,
The expression for the final radius by equating the volume is given as,
The expression for the forging force is given as,
Here,
The expression for the average pressure is given as,
The expression for final height for
The expression for final height for
The expression for final height for
The expression for final height for
The expression for final height for
Calculation:
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
| Reduction (in | Forging force (in |
The plot between forging force and reduction in height is shown in figure (1) below,

Figure (1)
(b)
The force vs. reduction in height curve in open die forging of cylinder for
(b)
Explanation of Solution
Given:
The initial thickness of the specimen is
The initial diameter of the specimen is
The friction coefficient is
The velocity of the hydraulic press is
Formula used:
The expression for the flow stress is given as,
Here,
The expression for the true strain is given as,
Here,
The expression for the final radius by equating the volume is given as,
The expression for the forging force is given as,
Here,
The expression for the average pressure is given as,
The expression for final height for
The expression for final height for
The expression for final height for
The expression for final height for
The expression for final height for
Calculation:
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
The final height can be calculated as,
The final radius can be calculated as,
The true strain can be calculated as,
The flow stress can be calculated as,
Refer to table 2.2 “Typical values of strength coefficient
The average pressure can be calculated as,
The forging force can be calculated as,
For
| Reduction (in | Forging force (in |
The plot between forging force and reduction in height is shown in figure (2) below,
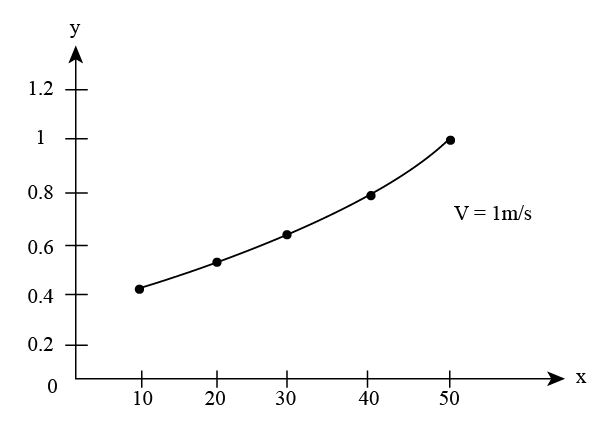
Figure (2)
Want to see more full solutions like this?
Chapter 6 Solutions
Pearson eText for Manufacturing Processes for Engineering Materials -- Instant Access (Pearson+)
- A small electronic package with a surface area of 820 cm2 is placed in a room where the airtemperature is 28 o C. The heat transfer coefficient is 7.3 W/m2 - o C. You are asked to determine if it isjustified to neglect heat loss from the package by radiation. Assume a uniform surface temperature of78 o C and surface emissivity of 0.65 Assume further that room’s walls and ceiling are at a uniformtemperature of 16 o C.arrow_forwardA hollow metal sphere of outer radius or = 2 cm is heated internally with a variable output electricheater. The sphere loses heat from its surface by convection and radiation. The heat transfercoefficient is 22 W/ m2 - o C and surface emissivity is 0.92. The ambient fluid temperature is 20 o C andthe surroundings temperature is 14 oC. Construct a graph of the surface temperature corresponding toheating rates ranging from zero to 100 watts. Assume steady state. Use a simplified model forradiation exchange based on a small gray surface enclosed by a much larger surface at 14 o C.arrow_forward2. A program to make the part depicted in Figure 26.A has been created, presented in figure 26.B, but some information still needs to be filled in. Compute the tool locations, depths, and other missing information to present a completed program. (Hint: You may have to look up geometry for the center drill and standard 0.5000 in twist drill to know the required depth to drill). Dashed line indicates - corner of original stock Intended toolpath-tangent - arc entry and exit sized to programmer's judgment 026022 (Slot and Drill Part) (Setup Instructions. (UNITS: Inches (WORKPIECE MAT'L: SAE 1020 STEEL (Workpiece: 3.25 x 2.00 x0.75 in. Plate (PRZ Location G54: ( XY 0.0 Upper Left of Fixture ( TOP OF PART 2-0 (Tool List: ) ( T04 T02 0.500 IN 4 FLUTE FLAT END MILL) #4 CENTER DRILL ' T02 0.500 TWIST DRILL N010 GOO G90 G17 G20 G49 G40 G80 G54 N020 M06 T02 (0.5 IN 4-FLUTE END MILL) R0.750 N030 S760 M03 G00 x N040 043 H02 2 Y (P1) (RAPID DOWN -TLO) P4 NO50 MOB (COOLANT ON) N060 G01 X R1.000 N070…arrow_forward
- 6–95. The reaction of the ballast on the railway tie can be assumed uniformly distributed over its length as shown. If the wood has an allowable bending stress of σallow=1.5 ksi, determine the required minimum thickness t of the rectangular cross section of the tie to the nearest 18 in. Please include all steps. Also if you can, please explain how you found Mmax using an equation rather than using just the moment diagram. Thank you!arrow_forward6–53. If the moment acting on the cross section is M=600 N⋅m, determine the resultant force the bending stress produces on the top board. Please explain each step. Please explain how you got the numbers and where you plugged them in to solve the problem. Thank you!arrow_forwardSolving coplanar forcesarrow_forward
- Complete the following problems. Show your work/calculations, save as.pdf and upload to the assignment in Blackboard. 1. What are the x and y dimensions for the center position of holes 1,2, and 3 in the part shown in Figure 26.2 (below)? 6.0000 7118 Zero reference point 1.0005 1.0000 1.252 Bore C' bore 1.250 6.0000 .7118 0.2180 deep (3 holes) 2.6563 1.9445 3.000 diam. slot 0.3000 deep. 0.3000 wide 2.6563 1.9445arrow_forwardComplete the following problems. Show your work/calculations, save as.pdf and upload to the assignment in Blackboard. missing information to present a completed program. (Hint: You may have to look up geometry for the center drill and standard 0.5000 in twist drill to know the required depth to drill). 1. What are the x and y dimensions for the center position of holes 1,2, and 3 in the part shown in Figure 26.2 (below)? 6.0000 Zero reference point 7118 1.0005 1.0000 1.252 Bore 6.0000 .7118 Cbore 0.2180 deep (3 holes) 2.6563 1.9445 Figure 26.2 026022 (8lot and Drill Part) (Setup Instructions--- (UNITS: Inches (WORKPIECE NAT'L SAE 1020 STEEL (Workpiece: 3.25 x 2.00 x0.75 in. Plate (PRZ Location 054: ' XY 0.0 - Upper Left of Fixture TOP OF PART 2-0 (Tool List ( T02 0.500 IN 4 FLUTE FLAT END MILL #4 CENTER DRILL Dashed line indicates- corner of original stock ( T04 T02 3.000 diam. slot 0.3000 deep. 0.3000 wide Intended toolpath-tangent- arc entry and exit sized to programmer's judgment…arrow_forwardA program to make the part depicted in Figure 26.A has been created, presented in figure 26.B, but some information still needs to be filled in. Compute the tool locations, depths, and other missing information to present a completed program. (Hint: You may have to look up geometry for the center drill and standard 0.5000 in twist drill to know the required depth to drill).arrow_forward
- We consider a laminar flow induced by an impulsively started infinite flat plate. The y-axis is normal to the plate. The x- and z-axes form a plane parallel to the plate. The plate is defined by y = 0. For time t <0, the plate and the flow are at rest. For t≥0, the velocity of the plate is parallel to the 2-coordinate; its value is constant and equal to uw. At infinity, the flow is at rest. The flow induced by the motion of the plate is independent of z. (a) From the continuity equation, show that v=0 everywhere in the flow and the resulting momentum equation is მu Ət Note that this equation has the form of a diffusion equation (the same form as the heat equation). (b) We introduce the new variables T, Y and U such that T=kt, Y=k/2y, U = u where k is an arbitrary constant. In the new system of variables, the solution is U(Y,T). The solution U(Y,T) is expressed by a function of Y and T and the solution u(y, t) is expressed by a function of y and t. Show that the functions are identical.…arrow_forwardPart A: Suppose you wanted to drill a 1.5 in diameter hole through a piece of 1020 cold-rolled steel that is 2 in thick, using an HSS twist drill. What values if feed and cutting speed will you specify, along with an appropriate allowance? Part B: How much time will be required to drill the hole in the previous problem using the HSS drill?arrow_forward1.1 m 1.3 m B 60-mm diameter Brass 40-mm diameter Aluminum PROBLEM 2.52 - A rod consisting of two cylindrical portions AB and BC is restrained at both ends. Portion AB is made of brass (E₁ = 105 GPa, α = 20.9×10°/°C) and portion BC is made of aluminum (Ę₁ =72 GPa, α = 23.9×10/°C). Knowing that the rod is initially unstressed, determine (a) the normal stresses induced in portions AB and BC by a temperature rise of 42°C, (b) the corresponding deflection of point B.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





