Chapter 6, Problem 64QP

Summary Introduction

To calculate: The annual percentage rate and the effective annual rate of the two loans.

Introduction:

The annual rate that is earned from an investment or charged for borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is computed by multiplying the interest rate per period with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.

Answer to Problem 64QP

The annual percentage rate is 5.50% and the effective annual rates for the two loans are 5.98% and 9.01%

Explanation of Solution

Given information:

An area has two banks, Bank I and Bank IMG. The banks offer a thirty year mortgage loan of $220,000 at 5.5%, and the banks charge an application fee of $3,500. The application fee that the Bank I charges is refundable if there is a denial for the loan application. The Bank IMG does not refund the application fee if the loan is denied.

The current disclosure law needs that any fee that is refundable for the rejection of the applicant will be included in calculating the annual percentage rate. However, this is not needed for the nonrefundable fees.

Note: First, it is necessary to calculate the annual percentage rate and the effective annual rate with the refundable fee. It is necessary to utilize the loan’s actual cash flow to determine the rate of interest. The actual application fee is $3,500 and so Person X has to borrow $223,500 to get $220,000 after the fee deduction.

Formula to calculate the present value annuity:

$\text{Present value annuity}=C\left\{\frac{\left[1-\left(\frac{1}{1+r^t}\right)\right]}{r}\right\}$

Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period. The payment is found using the formulae of the present value of annuity.

Compute the present value annuity:

$\begin{array}{c}\text{Present value annuity}=\text{C}\left\{\frac{\left[1-\left(\frac{1}{{\left(1+r\right)}^t}\right)\right]}{r}\right\}\\ \$223,500=\text{C}\left\{\frac{\left[1-\left(\frac{1}{{\left(1+\left(\frac{0.055}{12}\right)\right)}^{360}}\right)\right]}{\frac{0.055}{12}}\right\}\\ \$223,500=\text{C}\left\{\frac{\left[1-\left(\frac{1}{{\left(1+0.004\right)}^{360}}\right)\right]}{0.004583333}\right\}\\ \$223,500=\text{C}\left\{\frac{\left[1-0.192775252\right]}{0.00458333}\right\}\end{array}$

$\begin{array}{c}\$223,500=\text{C}\left\{\frac{\left[1-0.192775252\right]}{0.004583333}\right\}\\ \$223,500=176.1217759\text{C}\\ \text{C}=\$1,269.008326\end{array}$

Hence, the payment C is $1,269.008.

Note: The r values is found using the calculated C amount in the equation of the present value of annuity and the original amount that has to be borrowed that is $223,500.

Formula to calculate the present value annuity:

$\text{Present value annuity}=C\left\{\frac{\left[1-\left(\frac{1}{1+r^t}\right)\right]}{r}\right\}$

Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period.

Compute the present value annuity:

$\begin{array}{c}\text{Present value annuity}=\text{C}\left\{\frac{\left[1-\left(\frac{1}{{\left(1+r\right)}^t}\right)\right]}{r}\right\}\\ \$223,500=\$1,269.008\left\{\frac{\left[1-\left(\frac{1}{{\left(1+r\right)}^{360}}\right)\right]}{r}\right\}\end{array}$

Note: To find the interest rate, it is necessary to solve the equation using a spreadsheet.

Compute the interest rate using the spreadsheet:

Step 1:

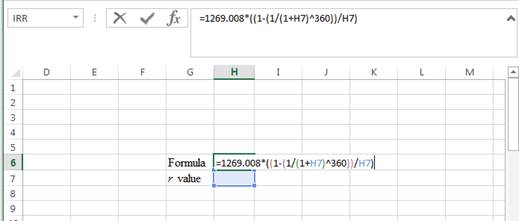
• Type the formula of the present value annuity in H6 in the spreadsheet and consider the r value as H7.

Step 2:

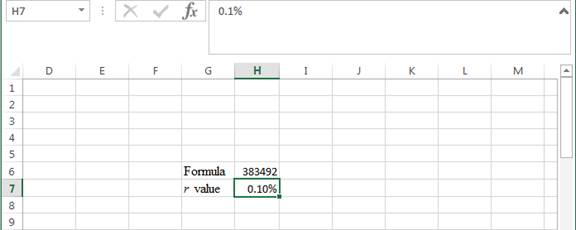
• Assume the r value as 0.10%.

Step 3:

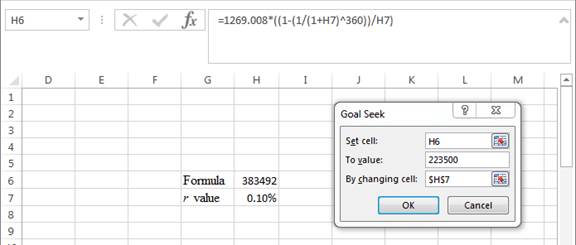
• In the spreadsheet, go to Data and select What-If-Analysis.
• Under What-If-Analysis tab, select Goal Seek.
• In set cell, select H6 (the formula).
• The ‘To value’ is considered as 223,500 (the value of the present value of annuity).
• The H7 cell is selected for the 'by changing cell'.

Step 4:

• Following the previous step, click OK in the Goal Seek Status. The Goal Seek Status appears with the r value.

Step 5:

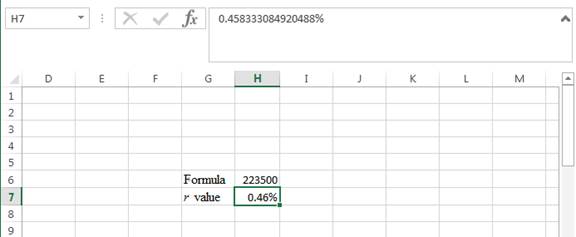
• The r value appears to be 0.458333084920488%.

Hence, the r value is 0.46%

Compute the annual percentage rate:

$\begin{array}{c}\text{APR}=12\left(0.4583\%\right)\\ =5.50\%\end{array}$

Note: The annual percentage rate is computed by multiplying the interest rate with the number of periods in a year.

Hence, the annual percentage rate is 5.50%.

Formula to calculate the effective annual rate:

$\text{Effective annual rate}=\left(1+{\left(\frac{\text{APR}}{12}\right)}^{12}-1\right)$

Compute the effective annual rate:

$\begin{array}{c}\text{Effective annual rate}=\left(1+{\left(\frac{\text{APR}}{12}\right)}^{12}-1\right)\\ ={\left(1+0.004853\right)}^{12}-1\\ ={\left(1.004122\right)}^{12}-1\\ =0.0598\%\end{array}$

Hence, the effective annual rate is 0.0598% or 5.98%.

Calculations for the nonrefundable fee:

Annual percentage rate is 5.5%

Note: The annual percentage rate for the nonrefundable fee is the quoted rate, as the fee is not considered as a part of the loan. The effective annual rate is computed with the help of the annual percentage rate.

Formula to calculate the effective annual rate:

$\text{Effective annual rate}=\left(1+{\left(\frac{\text{APR}}{12}\right)}^{12}-1\right)$

Compute the effective annual rate:

$\begin{array}{c}\text{Effective annual rate}=\left(1+{\left(\frac{\text{APR}}{12}\right)}^{12}-1\right)\\ ={\left(1+0.055\right)}^{12}-1\\ ={\left(1.055\right)}^{12}-1\\ =0.901\%\end{array}$

Hence, the effective annual rate for the non-refundable fee is 0.901% or 9.01%.