PHYSICS 1250 PACKAGE >CI<
9th Edition
ISBN: 9781305000988
Author: SERWAY
Publisher: CENGAGE LEARNING (CUSTOM)
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6, Problem 6.4OQ
A pendulum consists of a small object called a bob hanging from a light cord of fixed length, with the top end of the cord fixed, as represented in Figure OQ6.4. The bob moves without friction, swinging equally high on both sides. It moves from its turning point A through point B and reaches its maximum speed at point C. (a) Of these points, is there a point where the bob has nonzero radial acceleration and zero tangential acceleration? If so, which point? What is the direction of its total acceleration at (his point? (b) Of these points, is there a point where the bob has nonzero tangential acceleration and zero radial acceleration? If so, which point? What is the direction of its total acceleration at this point? (c) Is there a point where the bob has no acceleration? If so, which point? (d) Is there a point where the bob has both nonzero tangential and radial acceleration? If so, which point? What is the direction of its total acceleration at this point?
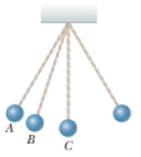
Figure OQ6.4
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A light, rigid rod is 77.0 cm long. Its top end is pivoted on a frictionless, horizontal axle. The rod hangs straight down at rest with a small, massive ball attached to its bottom end. You strike the ball, suddenly giving it a horizontal velocity so that it swings around in a full circle. What minimum speedat the bottom is required to make the ball go over the top of the circle?
Answer : 5.49 m/s
A rod of length L=3.00 m and negligible mass, that can pivot about one end to rotate in a vertical circle. A ball of mass m = 10.0 kg is attached to the other end. The rod is pulled aside to angle θ0 = 70° and released with initial velocity ? = 5.00 m/s. (a) What is the speed of the ball at the lowest point? (b) what is the speed of the ball when θ = 10°?
A light, rigid rod is 68.5 cm long. Its top end is pivoted on a frictionless horizontal axle. The rod hangs straight down at rest with a small, massive ball attached to its bottom end. You strike the ball, suddenly giving it a horizontal velocity so that it swings around in a full circle. What minimum speed at the bottom is required to make the ball go over the top of the circle?
Chapter 6 Solutions
PHYSICS 1250 PACKAGE >CI<
Ch. 6 - You are riding on a Ferris wheel that is rotating...Ch. 6 - A bead slides at constant speed along a curved...Ch. 6 - Consider the passenger in the car making a left...Ch. 6 - A basketball and a 2-inch-diameter steel ball,...Ch. 6 - A child is practicing for a BMX race. His speed...Ch. 6 - Consider a skydive r who has stepped from a...Ch. 6 - A door in a hospital has a pneumatic closer that...Ch. 6 - A pendulum consists of a small object called a bob...Ch. 6 - As a raindrop falls through the atmosphere, its...Ch. 6 - An office door is given a sharp push and swings...
Ch. 6 - Before takeoff on an airplane, an inquisitive...Ch. 6 - What forces cause (a) an automobile, (b) a...Ch. 6 - A falling skydiver reaches terminal speed with her...Ch. 6 - An object executes circular motion with constant...Ch. 6 - Describe the path of a moving body in the event...Ch. 6 - The observer in the accelerating elevator of...Ch. 6 - Prob. 6.6CQCh. 6 - It has been suggested dial rotating cylinders...Ch. 6 - Consider a small raindrop and a large raindrop...Ch. 6 - Why does a pilot lend to black out when pulling...Ch. 6 - Prob. 6.10CQCh. 6 - If the current position and velocity of every...Ch. 6 - A light string can support a stationary hanging...Ch. 6 - Whenever two Apollo astronauts were on the surface...Ch. 6 - In the Bohr model of the hydrogen atom, an...Ch. 6 - A curve in a road forms part of a horizontal...Ch. 6 - In a cyclotron (one type of particle accelerator),...Ch. 6 - A car initially traveling eastward turns north by...Ch. 6 - A space station, in the form of a wheel 120 m in...Ch. 6 - Consider a conical pendulum (Fig. P6.8) with a bob...Ch. 6 - A coin placed 30.0 cm from the center of a...Ch. 6 - Why is the following situation impossible? The...Ch. 6 - A crate of eggs is located in the middle of the...Ch. 6 - A pail of water is rotated in a vertical circle of...Ch. 6 - A hawk flies in a horizontal arc of radius 12.0 m...Ch. 6 - A 40.0-kg child swings in a swing supported by two...Ch. 6 - A child of mass m swings in a swing supported by...Ch. 6 - A roller-coaster car (Fig. P6.16) has a mass of...Ch. 6 - A roller coaster at the Six Flags Great America...Ch. 6 - One end of a cord is fixed and a small 0.500-kg...Ch. 6 - Prob. 6.19PCh. 6 - An object of mass m = 5.00 kg, attached to a...Ch. 6 - All object of mass m = 500 kg is suspended from...Ch. 6 - A child lying on her back experiences 55.0 N...Ch. 6 - A person stands on a scale in an elevator. As the...Ch. 6 - Review. A student, along with her backpack on the...Ch. 6 - A small container of water is placed on a...Ch. 6 - Review. (a) Estimate the terminal speed of a...Ch. 6 - The mass of a sports car is 1 200 kg. The shape of...Ch. 6 - A skydiver of mass 80.0 kg jumps from a...Ch. 6 - Calculate the force required to pull a copper ball...Ch. 6 - A small piece of Styrofoam packing material is...Ch. 6 - Prob. 6.31PCh. 6 - Prob. 6.32PCh. 6 - Assume the resistive force acting on a speed...Ch. 6 - Review. A window washer pulls a rubber squeegee...Ch. 6 - A motorboat cuts its engine when its speed is 10.0...Ch. 6 - You can feel a force of air drag on your hand if...Ch. 6 - A car travels clockwise at constant speed around a...Ch. 6 - The mass of a roller-coaster car, including its...Ch. 6 - A string under a tension of 50.0 N is used to...Ch. 6 - Disturbed by speeding cars outside his workplace,...Ch. 6 - A car of mass m passes over a hump in a road that...Ch. 6 - A childs toy consists of a small wedge that has an...Ch. 6 - A seaplane of total mass m lands on a lake with...Ch. 6 - An object of mass m1 = 4.00 kg is tied to an...Ch. 6 - A ball of mass m = 0.275 kg swings in a vertical...Ch. 6 - Why is the following situation impossible? A...Ch. 6 - (a) A luggage carousel at an airport has the form...Ch. 6 - In a home laundry dryer, a cylindrical tub...Ch. 6 - Prob. 6.49APCh. 6 - A basin surrounding a drain has the shape of a...Ch. 6 - A truck is moving with constant acceleration a up...Ch. 6 - The pilot of an airplane executes a loop-the-loop...Ch. 6 - Review. While learning to drive, you arc in a 1...Ch. 6 - A puck of mass m1 is tied to a string and allowed...Ch. 6 - Because the Earth rotates about its axis, a point...Ch. 6 - Galileo thought about whether acceleration should...Ch. 6 - Figure P6.57 shows a photo of a swing a ride at an...Ch. 6 - Review. A piece of putty is initially located at...Ch. 6 - An amusement park ride consists of a large...Ch. 6 - Members of a skydiving club were given the...Ch. 6 - A car rounds a banked curve as discussed in...Ch. 6 - In Example 6.5, we investigated the forces a child...Ch. 6 - A model airplane of mass 0.750 kg flies with a...Ch. 6 - A student builds and calibrates an accelerometer...Ch. 6 - A 9.00-kg object starting from rest falls through...Ch. 6 - For t 0, an object of mass m experiences no force...Ch. 6 - A golfer tees off from a location precisely at i =...Ch. 6 - A single bead can slide with negligible friction...Ch. 6 - Prob. 6.69CPCh. 6 - Because of the Earths rotation, a plumb bob does...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A bicycle is turned upside down while its owner repairs a flat tire. A friend spins the other wheel and observes that drops of water fly off tangentially. She measures the heights reached by drops mov- ing vertically (Fig. P7.8). A drop that breaks loose from the tire on one turn rises vertically 54.0 cm above the tangent point. A drop that breaks loose on the next turn Figure P7.8 rises 51.0 cm above the tangent point. The radius of the wheel is 0.381 m. (a) Why does the first drop rise higher than the second drop? (b) Neglecting air friction and using only the observed heights and the radius of the wheel, find the wheel's angular acceleration (assuming it to be constant). Problems 8 and 69.arrow_forwardA 148 g ball is released from rest H = 1.51 m above the bottom track. It rolls down a straight 45° segment, then back up a parabolic segment whose shape is given by y = x2/4, where x and y are in m. How high will the ball go on the right before reversing direction and rolling back down?arrow_forwardA hollow sphere (I=2/3mr^2) of radius R rotates about a diameter with an angular speed ω. The sphere then collapses (magically) under the action of internal forces to a final radius of R/2 with no change in its mass. What is the final angular speed of the sphere? The answer is 4ω but I'm not sure how to get there.arrow_forward
- NZM.11 An unpowered roller-coaster car starts at rest at the top of a hill of height H, rolls down the hill, and then goes around a vertical loop of radius R. Determine the minimum value for H required if the car is to stay on the track at the top of the loop. (Hints: At the top of the loop, the car is upside down. If it is in contact with the track, though, the contact interaction will exert a normal force on the car perpendicular to the track and away from the track, since the normal force is a compression force. You may find it helpful to use conservation of energy here.)arrow_forwardOne end of a cord is fixed and a small 0.700-kg object is attached to the other end, where it swings in a section of a vertical circle of radius 1.00 m, as shown in the figure below. When θ = 21.0°, the speed of the object is 8.50 m/s. An object is swinging to the right and upward from the end of a cord attached to a horizontal surface. The cord makes an angle θ with the vertical. An arrow labeled vector v points in the direction of motion. (a) At this instant, find the magnitude of the tension in the string. N(b) At this instant, find the tangential and radial components of acceleration. at = m/s2 downward tangent to the circle ac = m/s2 inward (c) At this instant, find the total acceleration. inward and below the cord at °(d) Is your answer changed if the object is swinging down toward its lowest point instead of swinging up? YesNo (e) Explain your answer to part (d).arrow_forwardYou push a .50kg block against a spring (k=3100 N/m),compressing it by .12m. The block is then released from rest and the spring pushes the block away. The spring and the block lose contact and the block collides with a second block of twice the mass. The two blocks slide together down a frictionless track consisting of a flat straightaway and a vertical, semi-circle of radius 40cm. What is the speed of the blocks when they have travelled halfway up the semicircle part of the track? What is the magnitude of the normal force on the two blocks at that same location?arrow_forward
- In the figure here, a small, solid, uniform ball is to be shot from point P so that it rolls smoothly along a horizontal path, up along a ramp, and onto a plateau. Then it leaves the plateau horizontally to land on a game board, at a horizontal distance d from the right edge of the plateau. The vertical heights are h, to land at d = 6.5 cm? 5.0 cm and h, = 1.60 cm. With what speed must the ball be shot at point P for it -d- Ball 1.5 Vo m/s varrow_forwardA car initially traveling eastward turns north by traveling in a circular path at uniform speed as shown in Figure P7.15. The length of the arc ABC is 235 m, and the car completes the turn in 36.0 s. (a) Determine the car’s speed. (b) What is the magnitude and direction of the acceleration when the car is at point B?arrow_forwardOne end of a cord is fixed and a small 0.400-kg object is attached to the other end, where it swings in a section of a vertical circle of radius 1.50 m, as shown in the figure below. When θ = 23.0°, the speed of the object is 5.50 m/s. An object is swinging to the right and upward from the end of a cord attached to a horizontal surface. The cord makes an angle θ with the vertical. An arrow labeled vector v points in the direction of motion. (a) At this instant, find the magnitude of the tension in the string.N(b) At this instant, find the tangential and radial components of acceleration. at = m/s2 downward tangent to the circle ac = m/s2 inward (c) At this instant, find the total acceleration.inward and below the cord at °(d) Is your answer changed if the object is swinging down toward its lowest point instead of swinging up? YesNo (e) Explain your answer to part (d).arrow_forward
- One end of a cord is fixed and a small 0.400-kg object is attached to the other end, where it swings in a section of a vertical circle of radius 1.50 m, as shown in the figure below. When θ = 23.0°, the speed of the object is 5.50 m/s. An object is swinging to the right and upward from the end of a cord attached to a horizontal surface. The cord makes an angle θ with the vertical. An arrow labeled vector v points in the direction of motion. (a) At this instant, find the magnitude of the tension in the string.Your response is within 10% of the correct value. This may be due to roundoff error, or you could have a mistake in your calculation. Carry out all intermediate results to at least four-digit accuracy to minimize roundoff error. N(b) At this instant, find the tangential and radial components of acceleration. at = Your response differs from the correct answer by more than 100%. m/s2 downward tangent to the circle ac = Your response differs from the correct answer by more…arrow_forwardA 90 cm long rod rotates around the horizontal axis at one end. We raise the rod to the highest position and let it fall. With what angular speed is it moving at the lowest point?arrow_forwardA conical pendulum consists of a mass of 0.5 kg attached at one end of a sting. The other end is fixed. As the mass moves in a circular path of radius 0.7 m, the string traces out the surface of a cone. What is the angle that the string makes with the ceiling?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Mechanical work done (GCSE Physics); Author: Dr de Bruin's Classroom;https://www.youtube.com/watch?v=OapgRhYDMvw;License: Standard YouTube License, CC-BY