
Concept explainers
Find the equations for slope and deflection of the beam using direct integration method.
Answer to Problem 3P
The equation for slope for segment AB is
The equation for deflection for segment AB is
The equation for slope for segment BC is
The equation for deflection for segment BC is
Explanation of Solution
Calculation:
Draw the free body diagram of the beam as in Figure (1).
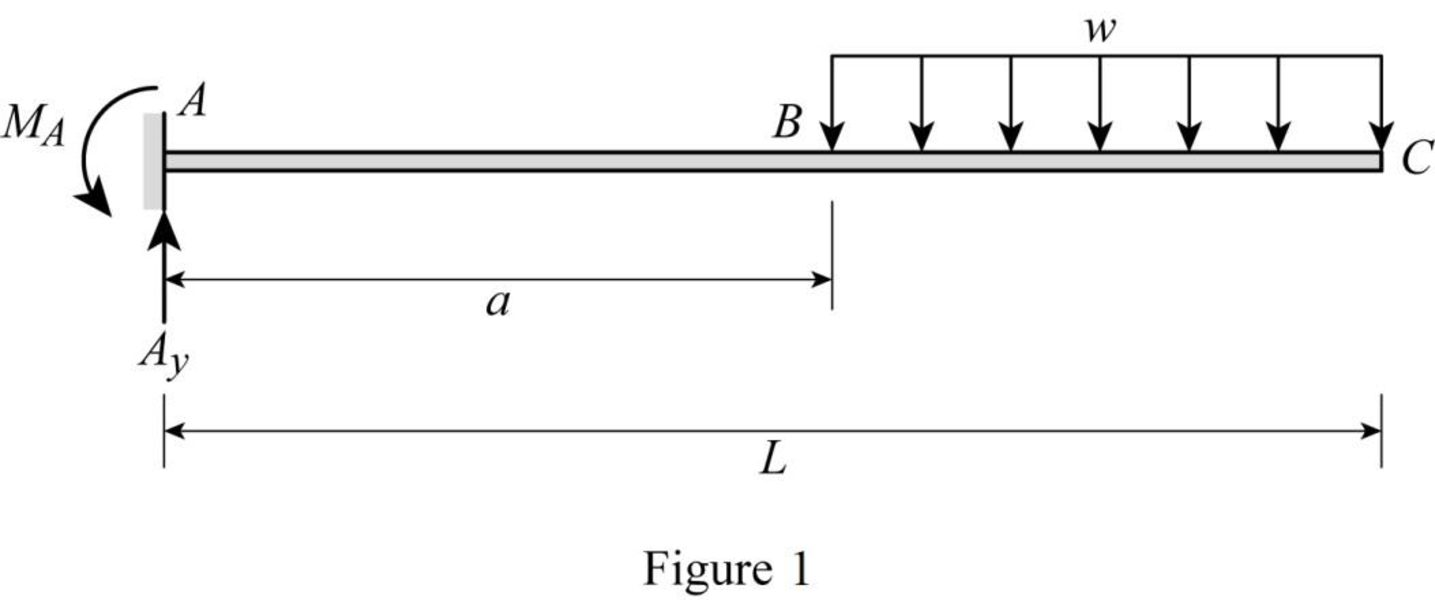
Refer Figure (1),
Find the reaction at support A.
Apply vertical equilibrium along y-axis.
Consider upward force as positive.
Find the moment at A.
Consider anticlockwise moment as positive.
Segment AB:
Consider a section
Sketch the free body diagram when section
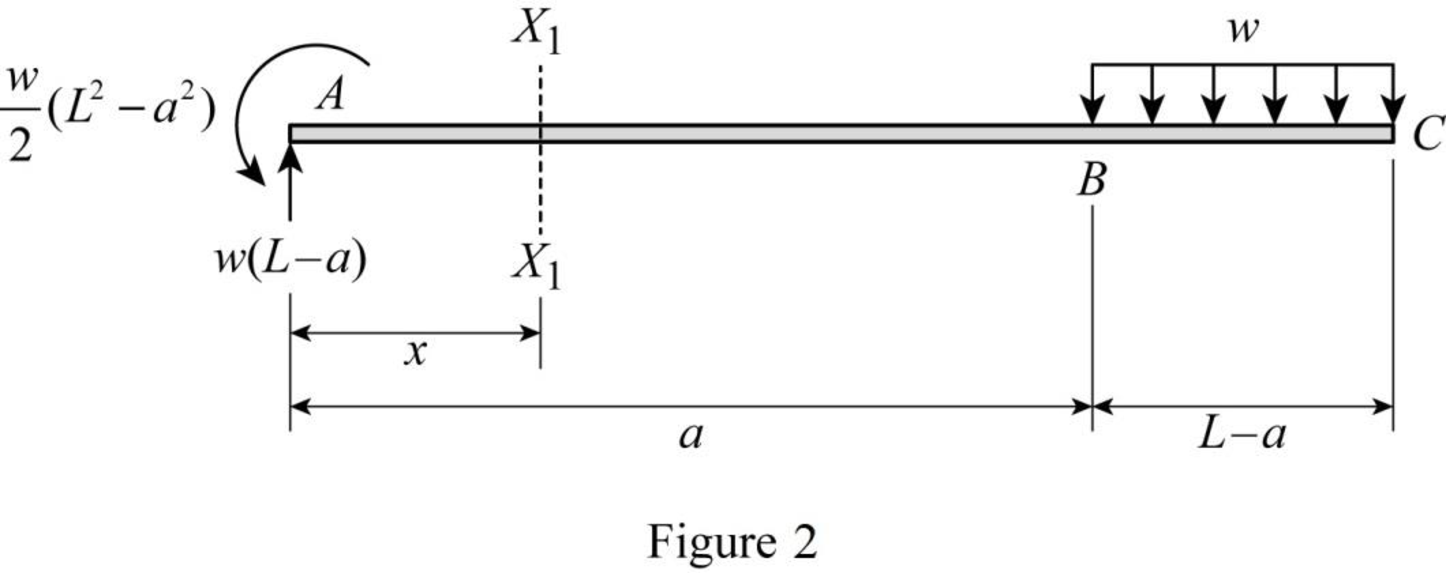
Refer Figure (2),
Take the moment at section
Write the equation for
Find the equation for slope
Integrate Equation (1) with respect to x.
Find the equation for deflection
Integrate again Equation (2) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (2):
At
Apply boundary conditions in Equation (1):
At
Find the equation for slope of segment AB.
Substitute 0 for
Thus, the equation for slope of segment AB is
Find the equation for deflection of segment AB.
Substitute 0 for
Thus, the equation for deflection is
Segment BC:
Consider a section
Sketch the free body diagram when section
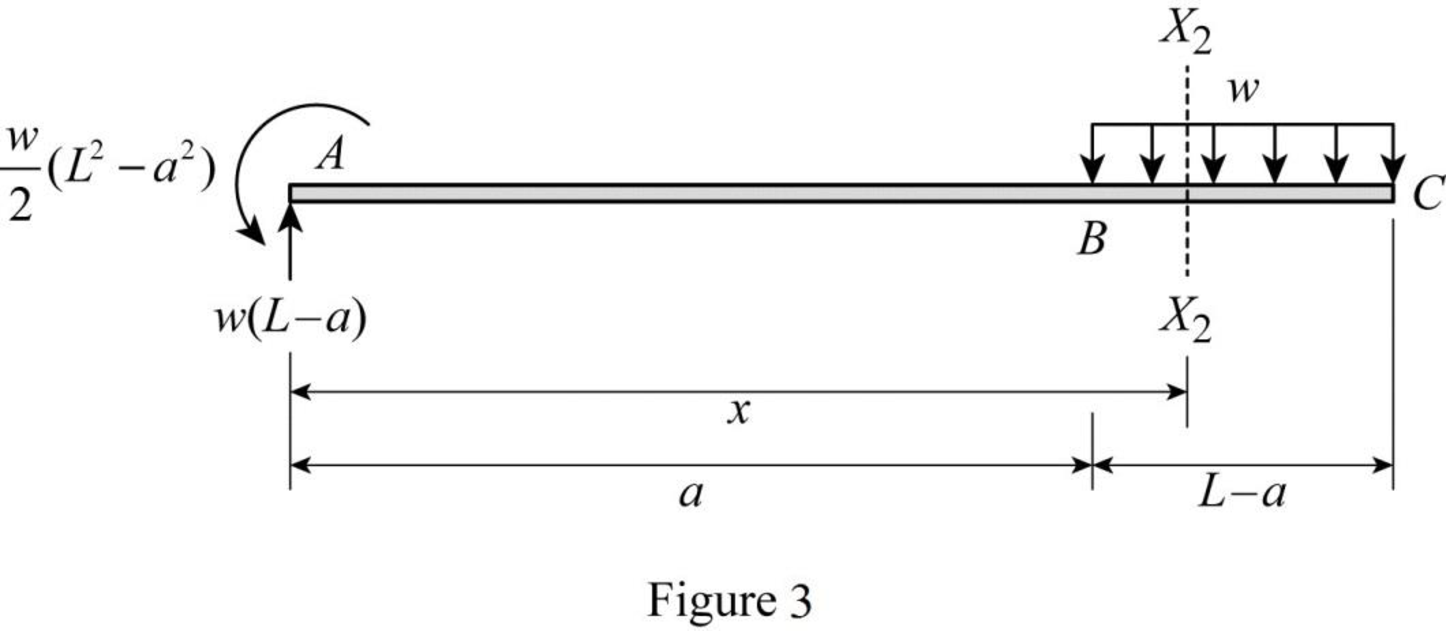
Refer Figure 3.
Write the equation for bending moment at section
Write the equation for
Write the equation for slope.
Integrate Equation (4) with respect to x.
Write the equation for deflection.
Integrate Equation (5) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (3):
At
Apply boundary conditions in Equation (4):
At
Find the equation for slope of segment BC.
Substitute
Thus, the equation for slope of segment BC is
Find the equation for deflection of segment BC.
Substitute
Thus, the equation for deflection of segment BC is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis, Si Edition
- I have the correct answer provided, just lookng for a more detailed breadown of how the answer was obtained thanks.arrow_forwardQ1. Statically indeterminate beam analysis. a) Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the moment distribution method. The beam is subjected to an UDL of w kN/m. L1= 0.4L. Assume the support at C is pinned, and A and B are roller supports. E = 200 GPa, I=250x106 mm². Use the values of w = 50 kN/m and L = 6 b) Draw the shear force and bending diagrams for the entire beam. c) Calculate the BMs at all the joints of the same beam shown in Fig.1 using the slope deflection method. d) Compare the values of BMs obtained using the two methods a) and c) and comment. w kN/m £1m Lm m Fig 1. Beam for Q1arrow_forwardI have the answer provided for the question, just looking for a more detailed breadown of how it was obtained thanks.arrow_forward
- Q5.--Finite-element-modelling. a) → Draw-a-2D-element-and-show-the dots (degrees of freedom). Draw-all-the-2D-elements. used-in-Strand 7..Explain the differences between-these-elements-in-terms-of-the-no..of. nodes-and-interpolation/shape-functions used. b)→A-8-m-x-8-m-plate (in-the-xx-plane)-with-8-mm-thickness, is fixed-at-all-the-edges.and.is. loaded-by-a-pressure-loading-of-4 kN/m2.-in-the-downward-(-2)-direction.-The-plate.is. made-of-steel-(E=-200 GPa, density-7850-kg/m3). Explain-the-steps-involved-in-setting. up-a-Strand 7-model-for-this-problem. Your-explanation-should-include-how-the-given. input-data-for-this-problem-will-be-used-in-Strand 7-modelling. Explain how you would. determine the maximum-deflection-from-the-Strand 7-output.-1 11arrow_forwardI need Help some hw for AutoCAD please use measure front top and side viewarrow_forwardCalculate the discharge of the system shown below. Neglecting minor losessarrow_forward
- Q3. Statically determinate or indeterminate beam analysis by the stiffness method a) Determine the global stiffness matrix of the beam shown in Fig. 3. Assume supports at 1 and 3 are rollers and the support at 2 is a pinned support. Indicate the degrees- of freedom in all the stiffness matrices. El is constant. Use the values of w = 50 kN/m and L1 = 2.0 m Note, L2-3L1. b) Determine the rotations at all the nodes of the beam and reactions at the supports. Show all calculations. c) Draw the BMD of the beam on the compression side showing the salient values. What are the maximum bending moments of the beam? Draw the deflected shape of the beam. d) Solve the problem using the Strand7. Assume any suitable value of El (state the value you have used for El). Show the model with all the nodes, element numbers and boundary conditions. Display the deflected shape and BMD. e) Show a table comparing the stiffness method (manual calculations) of the all the reactions and the maximum bending moment…arrow_forwardUsing AutoCAD. I need help please to exact measurearrow_forwardDraw Isometric view of this multiview of object.arrow_forward
- REMINDER: The truss must be cut into two different sections. You can choose either one to solve as you will get the same answer. Since there are three equations available, you can't cut more than three members 6.25 Determine the force in members BD, CD, and CE of the truss shown. BO C 36 kips 36 kips D F H 7.5 ft E G 4 panels at 10 ft = 40 ftarrow_forwardCalculate the area of the following polygon using the abscissa and projection method, taking into account the necessary adjustments before calculating the area of the polygon using the compass rule. Latitude Departure Side 930.63 N 930.63 S 1272 E 1271 W AB 122.14 E=12/2-1271-1 cr=-1 680 BC 173.83 length 591 CD 669.13 109.08 DE 139.36 961.1 EA 756.80 201.82 330.63/ 430.65 DEP=L SIN (O) >L DEP/SIN(O) LAT = L COS (0) DEPILATESIN(OYCOS (0)= TAN (0) O TAN-1 (DEP/LAT)= asztan Deptarrow_forwardEstimate the material quantities (cement, sand, gravel, and steel reinforcement) required for constructing 120 m concrete channel of the following typical cross section, concrete mix of 1:1.5:3 and thickness of 20 cm. Figure (1) Figure (1) 12250- 16300arrow_forward
