Chapter 6, Problem 32P

In the circuit in Fig. 6.64, let i_s = 4.5e^−2t mA and the voltage across each capacitor is equal to zero at t = 0. Determine v₁ and v₂ and the energy stored in each capacitor for all t > 0.

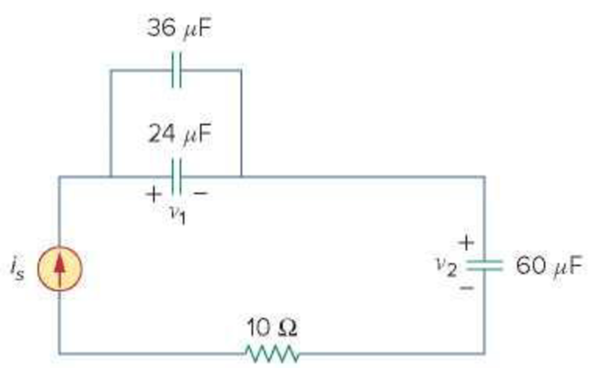
Figure 6.64

For Prob. 6.32.

To determine

Find the expression for the voltage $v_1$ and $v_2$ and the energy stored in each capacitor for all $t>0$.

Answer to Problem 32P

The expression for the voltage $v_1$ is $\left(37.5-37.5e^{-2t}\right)\text{V}$, $v_2$ is $\left(37.5-37.5e^{-2t}\right)\text{V}$ and the energy stored in the capacitor 1 $\left(w_1\right)$ is $25.31\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$, the capacitor 2 $\left(w_2\right)$ is $16.875\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$ and the capacitor 3 $\left(w_3\right)$ is $42.19\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$.

Explanation of Solution

Given data:

Refer to Figure 6.64 in the textbook.

The value of the current in the circuit $\left(i_s\right)$ is $4.5e^{-2t}\text{mA}$.

The voltage across the capacitor at $t=0$ $\left(v\left(t_0\right)\right)$ is $0\text{V}$.

Calculation:

The given circuit is redrawn as Figure 1.

Refer to Figure 1, the capacitors $C_1$ and $C_2$ are connected in parallel form.

Write the expression to calculate the equivalent capacitance for the parallel connected capacitors.

$C_{\text{eq}}=C_1+C_2$ (1)

Here,

$C_1$ is the value of the capacitor 1, and

$C_2$ is the value of the capacitor 2.

Substitute $36\mu \text{F}$ for $C_1$ and $24\mu \text{F}$ for $C_2$ in equation (1) to find $C_{\text{eq}}$.

$\begin{array}{c}{C}_{\text{eq}}=36\mu \text{F}+24\mu \text{F}\\ =60\mu \text{F}\end{array}$

The reduced circuit of the Figure 1 is drawn as Figure 2.

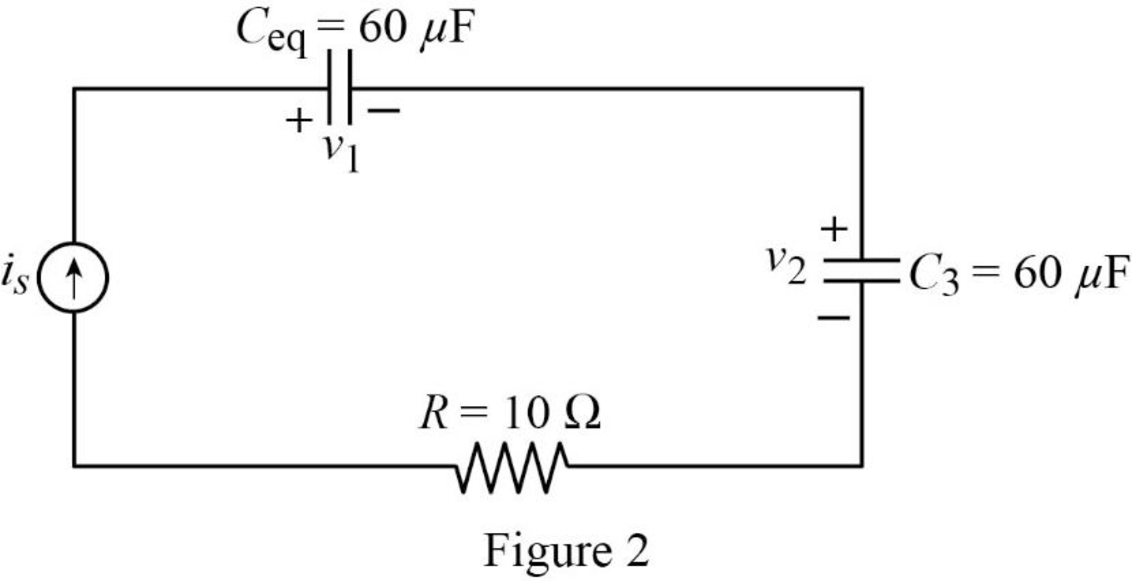
Write the expression to calculate the voltage across the equivalent capacitor $C_{\text{eq}}$ for $t>0$.

$v_1=\frac{1}{C_{\text{eq}}}{\displaystyle \underset{0}{\overset{t}{\int }}{i}_s}dt+v\left(t_0\right)$ (2)

Here,

$C_{\text{eq}}$ is the value of the equivalent capacitor,

$i_s$ is the value of the current, and

$v\left(t_0\right)$ is the voltage across the capacitor at $t=0$.

Substitute $60\mu \text{F}$ for $C_{\text{eq}}$, $4.5e^{-2t}\text{mA}$ for $i_s$ and $0\text{V}$ for $v\left(t_0\right)$ in equation (2) to find $v_1$.

$\begin{array}{c}{v}_1=\frac{1}{\left(60\mu \text{F}\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\left(4.5e^{-2t}\text{mA}\right)}dt+0\text{V}\\ =\frac{4.5\times {10}^{-3}}{60\times {10}^{-6}}{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-2t}}dt\frac{\text{A}}{\text{F}}\left\{\because 1\text{m}={\text{10}}^{-3},1\mu ={10}^{-6}\right\}\\ =75{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-2t}}dt\frac{\text{A}}{\text{F}}\end{array}$

Simplify the equation to find $v_1$.

$\begin{array}{c}{v}_1=75{\left[\frac{e^{-2t}}{-2}\right]}_0^t\frac{\text{A}\cdot \text{s}}{\text{F}}\\ =-37.5\left[e^{-2t}-e^{-2\left(0\right)}\right]\text{V}\left\{\because 1\text{V}=\frac{\text{1A}\cdot 1\text{s}}{\text{1F}}\right\}\\ =-37.5\left[e^{-2t}-1\right]\text{V}\left\{\because e^0=1\right\}\\ =\left[37.5-37.5e^{-2t}\right]\text{V}\end{array}$

Refer to Figure 2, the capacitors $C_{\text{eq}}$ and $C_3$ are connected in series form. The series connection of capacitors has equal charge. The capacitors with same capacitance value and charge have equal voltage value. Therefore, the voltage across both the capacitors $C_{\text{eq}}$ and $C_3$ are same. That is,

$v_1=v_2$ (3)

Substitute $\left[37.5-37.5e^{-2t}\right]\text{V}$ for $v_1$ in equation (3) to find $v_2$.

$v_2=\left[37.5-37.5e^{-2t}\right]\text{V}$

Refer to Figure 1, the capacitors $C_1$ and $C_2$ are connected in parallel form. For parallel connection, the voltage is same. Therefore the voltage across the capacitors $C_1$ and $C_2$ is $v_1$ and the voltage across the capacitor $C_3$ is $v_2$.

Write the expression to calculate the energy stored in the capacitor 1.

$w_1=\frac{1}{2}{C}_1{\left(v_1\right)}^2$ (4)

Here,

$v_1$ is the voltage across the capacitor 1.

Substitute $36\mu \text{F}$ for $C_1$ and $\left[37.5-37.5e^{-2t}\right]\text{V}$ for $v_1$ in equation (4) to find $w_1$.

$\begin{array}{c}{w}_1=\frac{1}{2}\left(36\mu \text{F}\right){\left(\left[37.5-37.5e^{-2t}\right]\text{V}\right)}^2\\ =\frac{1}{2}\left(36\times {10}^{-6}\right)\left({\left(37.5\right)}^2+{\left(37.5e^{-2t}\right)}^2-2\left(37.5\right)\left(37.5e^{-2t}\right)\right)\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =\frac{1}{2}\left(36\times {10}^{-6}\right)\left(1406.25+1406.25e^{-4t}-2812.5e^{-2t}\right)\text{J}\left\{1\text{J}=\text{1F}\cdot 1{\text{V}}^2\right\}\\ =\left(0.02531+0.02531e^{-4t}-0.05062e^{-2t}\right)\text{J}\end{array}$

Simplify the equation to find $w_1$.

$\begin{array}{c}{w}_1=0.02531\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =0.02531\times {10}^3\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =25.31\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =25.31\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Write the expression to calculate the energy stored in the capacitor 2.

$w_2=\frac{1}{2}{C}_2{\left(v_1\right)}^2$ (5)

Substitute $24\mu \text{F}$ for $C_2$ and $\left[37.5-37.5e^{-2t}\right]\text{V}$ for $v_1$ in equation (5) to find $w_2$.

$\begin{array}{c}{w}_2=\frac{1}{2}\left(24\mu \text{F}\right){\left(\left[37.5-37.5e^{-2t}\right]\text{V}\right)}^2\\ =\frac{1}{2}\left(24\times {10}^{-6}\right)\left({\left(37.5\right)}^2+{\left(37.5e^{-2t}\right)}^2-2\left(37.5\right)\left(37.5e^{-2t}\right)\right)\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =\frac{1}{2}\left(24\times {10}^{-6}\right)\left(1406.25+1406.25e^{-4t}-2812.5e^{-2t}\right)\text{J}\left\{1\text{J}=\text{1F}\cdot 1{\text{V}}^2\right\}\\ =\left(0.016875+0.016875e^{-4t}-0.03375e^{-2t}\right)\text{J}\end{array}$

Simplify the equation to find $w_2$.

$\begin{array}{c}{w}_2=0.016875\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =0.016875\times {10}^3\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =16.875\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =16.875\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Write the expression to calculate the energy stored in the capacitor 3.

$w_3=\frac{1}{2}{C}_3{\left(v_2\right)}^2$ (6)

Here,

$v_2$ is the voltage across the capacitor 3.

Substitute $60\mu \text{F}$ for $C_2$ and $\left[37.5-37.5e^{-2t}\right]\text{V}$ for $v_2$ in equation (6) to find $w_3$.

$\begin{array}{c}{w}_3=\frac{1}{2}\left(60\mu \text{F}\right){\left(\left[37.5-37.5e^{-2t}\right]\text{V}\right)}^2\\ =\frac{1}{2}\left(60\times {10}^{-6}\right)\left({\left(37.5\right)}^2+{\left(37.5e^{-2t}\right)}^2-2\left(37.5\right)\left(37.5e^{-2t}\right)\right)\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =\frac{1}{2}\left(60\times {10}^{-6}\right)\left(1406.25+1406.25e^{-4t}-2812.5e^{-2t}\right)\text{J}\left\{1\text{J}=\text{1F}\cdot 1{\text{V}}^2\right\}\\ =\left(0.04219+0.04219e^{-4t}-0.084375e^{-2t}\right)\text{J}\end{array}$

Simplify the equation to find $w_3$.

$\begin{array}{c}{w}_3=0.04219\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =0.04219\times {10}^3\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =42.19\times {10}^{-3}\left(1+e^{-4t}-2e^{-2t}\right)\text{J}\\ =42.19\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Conclusion:

Thus, the expression for the voltage $v_1$ is $\left(37.5-37.5e^{-2t}\right)\text{V}$, $v_2$ is $\left(37.5-37.5e^{-2t}\right)\text{V}$ and the energy stored in the capacitor 1 $\left(w_1\right)$ is $25.31\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$, the capacitor 2 $\left(w_2\right)$ is $16.875\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$ and the capacitor 3 $\left(w_3\right)$ is $42.19\left(1+e^{-4t}-2e^{-2t}\right)\text{mJ}$.