
For the graph shown in Fig. 6-19,
a. find three different Hamilton circuits.
b. find a Hamilton path that starts at A and ends at B.
c. find a Hamilton path that starts at D and ends at F.

(a)
To find:
Three Hamilton circuits for given graph.
Answer to Problem 1E
Solution:
The Hamilton circuit are
Explanation of Solution
Given:
The given figure is,
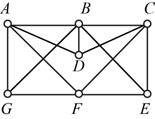
Approach:
A Hamilton circuit is the circuit that starts and ends at the same vertex and includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go to vertex B. From vertex B the options to move further are C, D, E, and G, go to vertex D. From vertex D the option to go forward is vertex C. From vertex C the option to move forward to is E. From vertex E the option to move forward to is F. From vertex F the option to move forward to is G. From vertex G the option to move forward to is A.
The Hamilton circuit is
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex G. From vertex G the options to move further are B and F, go forward with vertex B. From vertex B the options to go forward are vertices C, D, and E, go to vertex D. From vertex D the option to move forward to is C. From vertex C the option to move forward to is E. From vertex E the option to move forward to is F. From vertex F the option to move forward to is A.
The Hamilton circuit is
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex D. From vertex D the options to move further are B and C, go forward with vertex B. From vertex B the options to go forward are vertex C and E, go to vertex E. From vertex E the option to move forward to is C. From vertex C the option to move forward to is F. From vertex F the option to move forward to is G. From vertex G the option to move forward to is A.
The Hamilton circuit is
Conclusion:
Thus, the Hamilton circuits are
(b)
To find:
A Hamilton path that starts at A and ends at B.
Answer to Problem 1E
Solution:
A Hamilton path that starts at A and ends at B is
Explanation of Solution
Given:
The given figure is,

Approach:
A Hamilton path is the path that includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex G. From vertex G the options to move further are B and F, go forward with vertex F. From vertex F the options to go forward are vertex C, E, and G, go to vertex E. From vertex E the option to move forward to are B and C, go to vertex C. From vertex C the option to move forward to are B and D, go to vertex D. From vertex D the option to move forward to is B.
The Hamilton path is
Conclusion:
Thus, a Hamilton path that starts at A and ends at B is
(c)
To find:
A Hamilton path that starts at D and ends at F.
Answer to Problem 1E
Solution:
A Hamilton path that starts at D and ends at F is
Explanation of Solution
Given:
The given figure is,
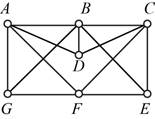
Approach:
A Hamilton path is the path that includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex D the options to go forward are vertices A, B, C, go forward with vertex C. From vertex C the options to move further are B, E and F, go forward with vertex E. From vertex E the options to go forward are vertex B and F, go to vertex B. From vertex B the option to move forward to are A and G, go to vertex G. From vertex G the option to move forward to are A and F, go to vertex A. From vertex A the option to move forward to is F.
The Hamilton path is
Conclusion:
Thus, a Hamilton path that starts at D and ends at F is
Want to see more full solutions like this?
Chapter 6 Solutions
EXCURSIONS IN MOD.MATH W/ACCESS >BI<
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
University Calculus
Elementary Statistics: A Step By Step Approach
Algebra and Trigonometry (6th Edition)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
- Problem #6 A special passcode to unlock your phone consists of 4 digits where repeated digits are not allowed. If someone were to randomly guess a 4 digit passcode, what is the probability that they guess your passcode on the first try?arrow_forwardProblem #3 If a card is picked at random from a standard 52-card deck, what is the probability of getting a black card or a queen?arrow_forwardProblem #1 In the 2010 census, it was reported that the United States had a population of 310 million people. Of those, 74 million were under the age of 18. If you chose a person from the U.S. population at random, what is the probability they are under the age of 18? Problem #2 Given a set S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, if you were choosing a number at random what is the probability that you would choose an even number or a number larger than 7?arrow_forward
- Find the tangential and normal components of the acceleration vector for the curve - F(t) = (2t, −3t³, −3+¹) at the point t = 1 - ā(1) = T + Ñ Give your answers to two decimal placesarrow_forwardFind the unit tangent vector to the curve defined by (t)=(-2t,-4t, √√49 - t²) at t = −6. T(−6) =arrow_forwardAnswer number twoarrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell

