Videos
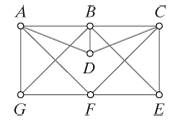
For the graph shown in Fig. 6-19,
a. find three different Hamilton circuits.
b. find a Hamilton path that starts at A and ends at B.
c. find a Hamilton path that starts at D and ends at F.
(a)
To find:
Three Hamilton circuits for given graph.
Answer to Problem 1E
Solution:
The Hamilton circuit are
Explanation of Solution
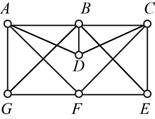
Given:
The given figure is,
Approach:
A Hamilton circuit is the circuit that starts and ends at the same vertex and includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go to vertex B. From vertex B the options to move further are C, D, E, and G, go to vertex D. From vertex D the option to go forward is vertex C. From vertex C the option to move forward to is E. From vertex E the option to move forward to is F. From vertex F the option to move forward to is G. From vertex G the option to move forward to is A.
The Hamilton circuit is
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex G. From vertex G the options to move further are B and F, go forward with vertex B. From vertex B the options to go forward are vertices C, D, and E, go to vertex D. From vertex D the option to move forward to is C. From vertex C the option to move forward to is E. From vertex E the option to move forward to is F. From vertex F the option to move forward to is A.
The Hamilton circuit is
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex D. From vertex D the options to move further are B and C, go forward with vertex B. From vertex B the options to go forward are vertex C and E, go to vertex E. From vertex E the option to move forward to is C. From vertex C the option to move forward to is F. From vertex F the option to move forward to is G. From vertex G the option to move forward to is A.
The Hamilton circuit is
Conclusion:
Thus, the Hamilton circuits are
(b)
To find:
A Hamilton path that starts at A and ends at B.
Answer to Problem 1E
Solution:
A Hamilton path that starts at A and ends at B is
Explanation of Solution
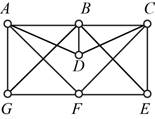
Given:
The given figure is,
Approach:
A Hamilton path is the path that includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex A the options to go forward are vertices B, D, F, and G, go forward with vertex G. From vertex G the options to move further are B and F, go forward with vertex F. From vertex F the options to go forward are vertex C, E, and G, go to vertex E. From vertex E the option to move forward to are B and C, go to vertex C. From vertex C the option to move forward to are B and D, go to vertex D. From vertex D the option to move forward to is B.
The Hamilton path is
Conclusion:
Thus, a Hamilton path that starts at A and ends at B is
(c)
To find:
A Hamilton path that starts at D and ends at F.
Answer to Problem 1E
Solution:
A Hamilton path that starts at D and ends at F is
Explanation of Solution
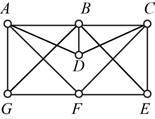
Given:
The given figure is,
Approach:
A Hamilton path is the path that includes every other vertex of the graph only once.
Calculation:
Let’s start with vertex D the options to go forward are vertices A, B, C, go forward with vertex C. From vertex C the options to move further are B, E and F, go forward with vertex E. From vertex E the options to go forward are vertex B and F, go to vertex B. From vertex B the option to move forward to are A and G, go to vertex G. From vertex G the option to move forward to are A and F, go to vertex A. From vertex A the option to move forward to is F.
The Hamilton path is
Conclusion:
Thus, a Hamilton path that starts at D and ends at F is
Want to see more full solutions like this?
Chapter 6 Solutions
Excursions in Modern Mathematics (9th Edition)
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
University Calculus
Elementary Statistics: A Step By Step Approach
Algebra and Trigonometry (6th Edition)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
- 30.3. Find and classify the isolated singularities of the following func- tions: (a). 23+1 22(2-1) (b). ²e¹/, (c). sin 3z (d). COS 2arrow_forward3. Consider the polynomial equation 6-iz+7z2-iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forwardDetermine the set of odd primes p for which 23 is a quadratic residue.arrow_forward
- Patterns in Floor Tiling A square floor is to be tiled with square tiles as shown. There are blue tiles on the main diagonals and red tiles everywhere else. In all cases, both blue and red tiles must be used. and the two diagonals must have a common blue tile at the center of the floor. If 81 blue tiles will be used, how many red tiles will be needed? For what numbers in place of 81 would this problem still be solvable? Find an expression in k giving the number of red tiles required in general.arrow_forwardSolve questionsarrow_forwardQ/ Find and classify the singularities of the functions- = 52+3 (1-2) sin² Z a fcz) b f(z) = tanz Z © f(2)= [z (e²-1)]arrow_forward
- The managing director of a consulting group has the accompanying monthly data on total overhead costs and professional labor hours to bill to clients. Complete parts a through c Overhead Costs Billable Hours345000 3000385000 4000410000 5000462000 6000530000 7000545000 8000arrow_forwardUsing the accompanying Home Market Value data and associated regression line, Market ValueMarket Valueequals=$28,416plus+$37.066×Square Feet, compute the errors associated with each observation using the formula e Subscript ieiequals=Upper Y Subscript iYiminus−ModifyingAbove Upper Y with caret Subscript iYi and construct a frequency distribution and histogram. Square Feet Market Value1813 911001916 1043001842 934001814 909001836 1020002030 1085001731 877001852 960001793 893001665 884001852 1009001619 967001690 876002370 1139002373 1131001666 875002122 1161001619 946001729 863001667 871001522 833001484 798001589 814001600 871001484 825001483 787001522 877001703 942001485 820001468 881001519 882001518 885001483 765001522 844001668 909001587 810001782 912001483 812001519 1007001522 872001684 966001581 86200arrow_forwardPatterns in Floor Tiling A square floor is to be tiled with square tiles as shown. There are blue tiles on the main diagonals and red tiles everywhere else. In all cases, both blue and red tiles must be used. and the two diagonals must have a common blue tile at the center of the floor. If 81 blue tiles will be used, how many red tiles will be needed?arrow_forward
- At a BBQ, you can choose to eat a burger, hotdog or pizza. you can choose to drink water, juice or pop. If you choose your meal at random, what is the probability that you will choose juice and a hot dog? What is the probability that you will not choose a burger and choose either water or pop?arrow_forwarda card is drawn from a standard deck of 52 cards. If a card is choosen at random, what is the probability that the card is a)heart b)a face card or c)a spade or 10arrow_forwardin a coffee shop, 160 customers came in. Of these, 60 bought coffe and cake and the rest ordered just coffee. determine the probability that the next person will buy coffee and cakearrow_forward
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell