Chapter 6, Problem 1CP

Specialty Toys

Specialty Toys, Inc., sells a variety of new and innovative children’s toys. Management learned that the preholiday season is the best time to introduce a new toy, because many families use this time to look for new ideas for December holiday gifts. When Specialty discovers a new toy with good market potential, it chooses an October market entry date.

In order to get toys in its stores by October, Specialty places one-time orders with its manufacturers in June or July of each year. Demand for children’s toys can be highly volatile. If a new toy catches on, a sense of shortage in the marketplace often increases the demand to high levels and large profits can be realized. However, new toys can also flop, leaving Specialty stuck with high levels of inventory that must be sold at reduced prices. The most important question the company faces is deciding how many units of a new toy should be purchased to meet anticipated sales demand. If too few are purchased, sales will be lost; if too many are purchased, profits will be reduced because of low prices realized in clearance sales.

For the coming season, Specialty plans to introduce a new product called Weather Teddy. This variation of a talking teddy bear is made by a company in Taiwan. When a child presses Teddy’s hand, the bear begins to talk. A built-in barometer selects one of five responses that predict the weather conditions. The responses range from “It looks to be a very nice day! Have fun” to “I think it may rain today. Don’t forget your umbrella.” Tests with the product show that, even though it is not a perfect weather predictor, its predictions are surprisingly good. Several of Specialty’s managers claimed Teddy gave predictions of the weather that were as good as many local television weather forecasters.

As with other products, Specialty faces the decision of how many Weather Teddy units to order for the coming holiday season. Members of the management team suggested order quantities of 15,000, 18,000, 24,000, or 28,000 units. The wide range of order quantities suggested indicates considerable disagreement concerning the market potential. The product management team asks you for an analysis of the stock-out probabilities for various order quantities, an estimate of the profit potential, and to help make an order quantity recommendation. Specialty expects to sell Weather Teddy for $24 based on a cost of $16 per unit. If inventory remains after the holiday season, Specialty will sell all surplus inventory for $5 per unit. After reviewing the sales history of similar products, Specialty’s senior sales forecaster predicted an expected demand of 20,000 units with a .95 probability that demand would be between 10,000 units and 30,000 units. Managerial Report

Prepare a managerial report that addresses the following issues and recommends an order quantity for the Weather Teddy product.

1. 1. Use the sales forecaster’s prediction to describe a normal probability distribution that can be used to approximate the demand distribution. Sketch the distribution and show its mean and standard deviation.
2. 2. Compute the probability of a stock-out for the order quantities suggested by members of the management team.
3. 3. Compute the projected profit for the order quantities suggested by the management team under three scenarios: worst case in which sales = 10,000 units, most likely case in which sales = 20,000 units, and best case in which sales = 30,000 units.
4. 4. One of Specialty’s managers felt that the profit potential was so great that the order quantity should have a 70% chance of meeting demand and only a 30% chance of any stock-outs. What quantity would be ordered under this policy, and what is the projected profit under the three sales scenarios?
5. 5. Provide your own recommendation for an order quantity and note the associated profit projections. Provide a rationale for your recommendation.

To determine

Describe a normal probability distribution that can be used to approximate the demand distribution using the sales forecaster’s prediction.

Sketch the distribution and show its mean and standard deviation.

Answer to Problem 1CP

The normal distribution with a mean of 20,000 and a standard deviation of 5,102 can be used to approximate the demand distribution using the sales forecaster’s prediction.

The normal probability distribution that can be used to approximate the demand distribution is shown below:

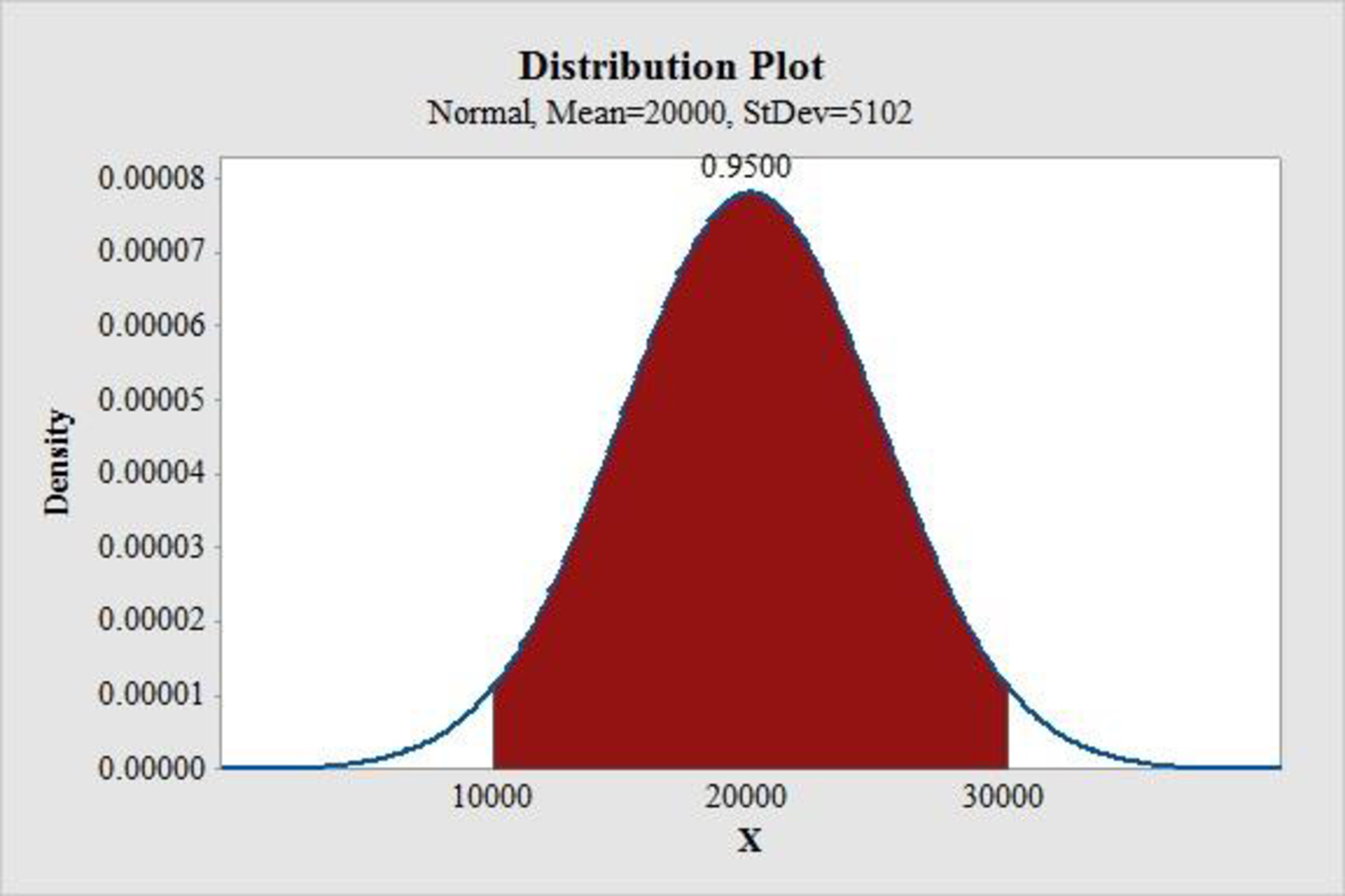
  Figure (1)

Explanation of Solution

Calculation:

The order quantities suggested are 15,000, 18,000, 24,000 or 28,000 units. The Weather Teddy is expected to be sold at $24 based on a cost of $16 per unit. All surplus inventories are sold at a cost of $5 per unit. The sales forecaster’s predicted that there will be an expected demand of 20,000 units with a 0.95 probability that demand would be between 10,000 units and 30,000 units.

Define the random variable x as the demand.

From the information provided by the forecaster, demand would be between 10,000 units and 30,000 units with a 0.95 probability.

Software Procedure:

Step-by-step procedure to obtain the z-values using the MINITAB software:

• Choose Graph > Probability Distribution Plot.
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 0 and Standard deviation as 1.
• Click the Shaded Area tab.
• Choose Probability and Both Tails for the region of the curve to shade.
• Enter the Probability value as 0.05.
• Click OK.

Output using the MINITAB software is given below:

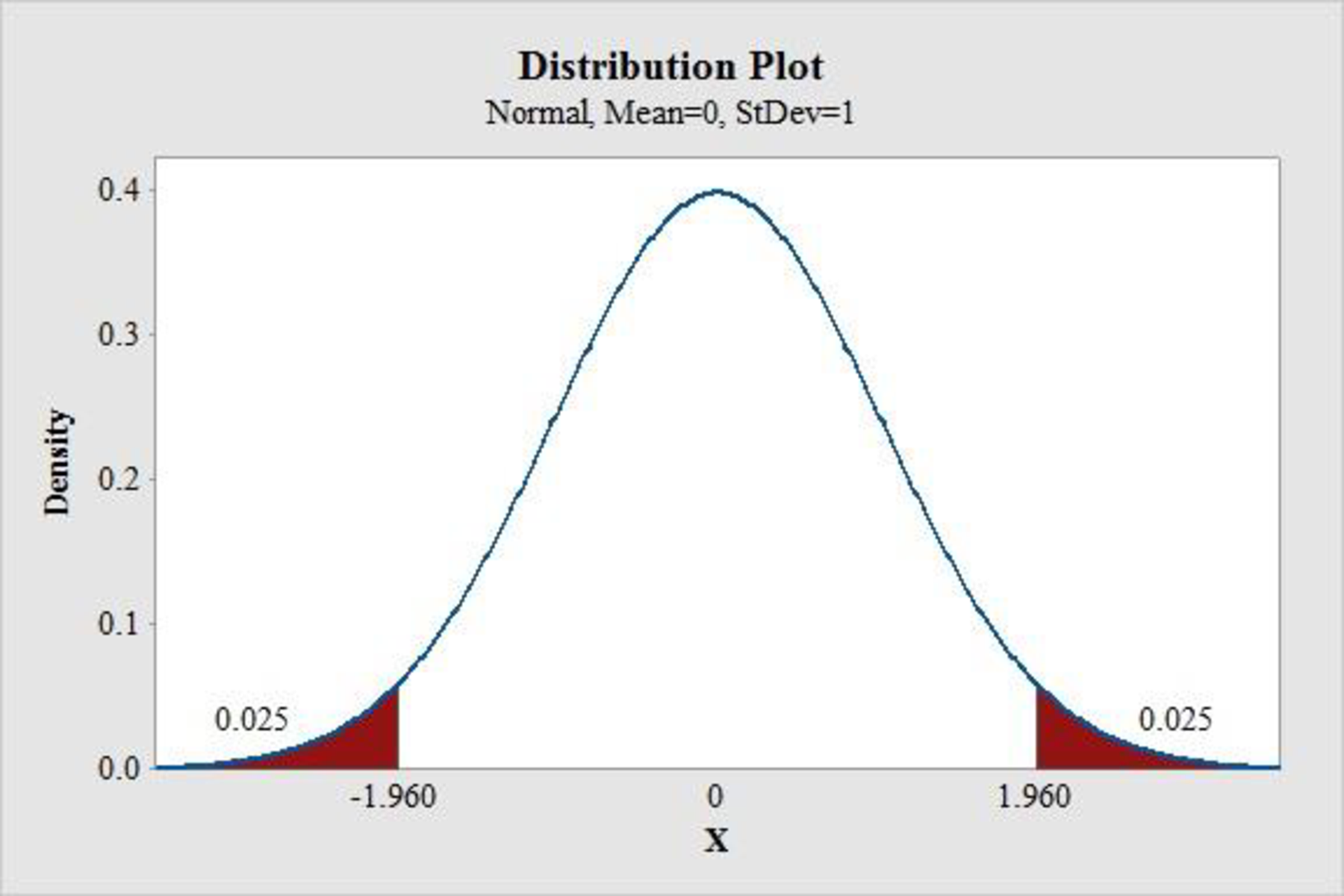
From the MINITAB output the z-values are –1.96 and 1.96.

The formula for z-score is,

$z=\frac{x-\mu }{\sigma }$

At $x=30,000$ for the given value, $\mu =20,000$ and $z=1.96$,

$\begin{array}{c}z=\frac{x-\mu }{\sigma }\\ 1.96=\frac{30,000-20,000}{\sigma }\\ \sigma =\frac{10,000}{1.96}\\ =5,102\end{array}$

Thus, the normal distribution with a mean of 20,000 and a standard deviation of 5,102 can be used to approximate the demand distribution using the sales forecaster’s prediction.

Software Procedure:

Step-by-step procedure to draw the normal curve using the MINITAB software:

• Choose Graph > Probability Distribution Plot.
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose X value and Middle area for the region of the curve to shade.
• Enter the as 0.05.
• Click OK.

The normal curve for demand is shown in figure (1).

To determine

Find the probability of a stock-out for the order quantities suggested by members of the management team.

Answer to Problem 1CP

The probability of a stock-out for the order quantity of 15,000 units is 0.8365.

The probability of a stock-out for the order quantity of 18,000 units is 0.6525.

The probability of a stock-out for the order quantity of 24,000 units is 0.2165.

The probability of a stock-out for the order quantity of 28,000 units is 0.05844.

Explanation of Solution

Calculation:

The probability of a stock-out for the order quantity of 15,000 units is $P\left(x>15,000\right)$.

Software Procedure:

Step-by-step procedure to obtain the probability value using the MINITAB software:

• Choose Graph > Probability Distribution Plot
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose X Value and Right Tail for the region of the curve to shade.
• Enter the X value as 15,000.
• Click OK.

Output using the MINITAB software is given below:

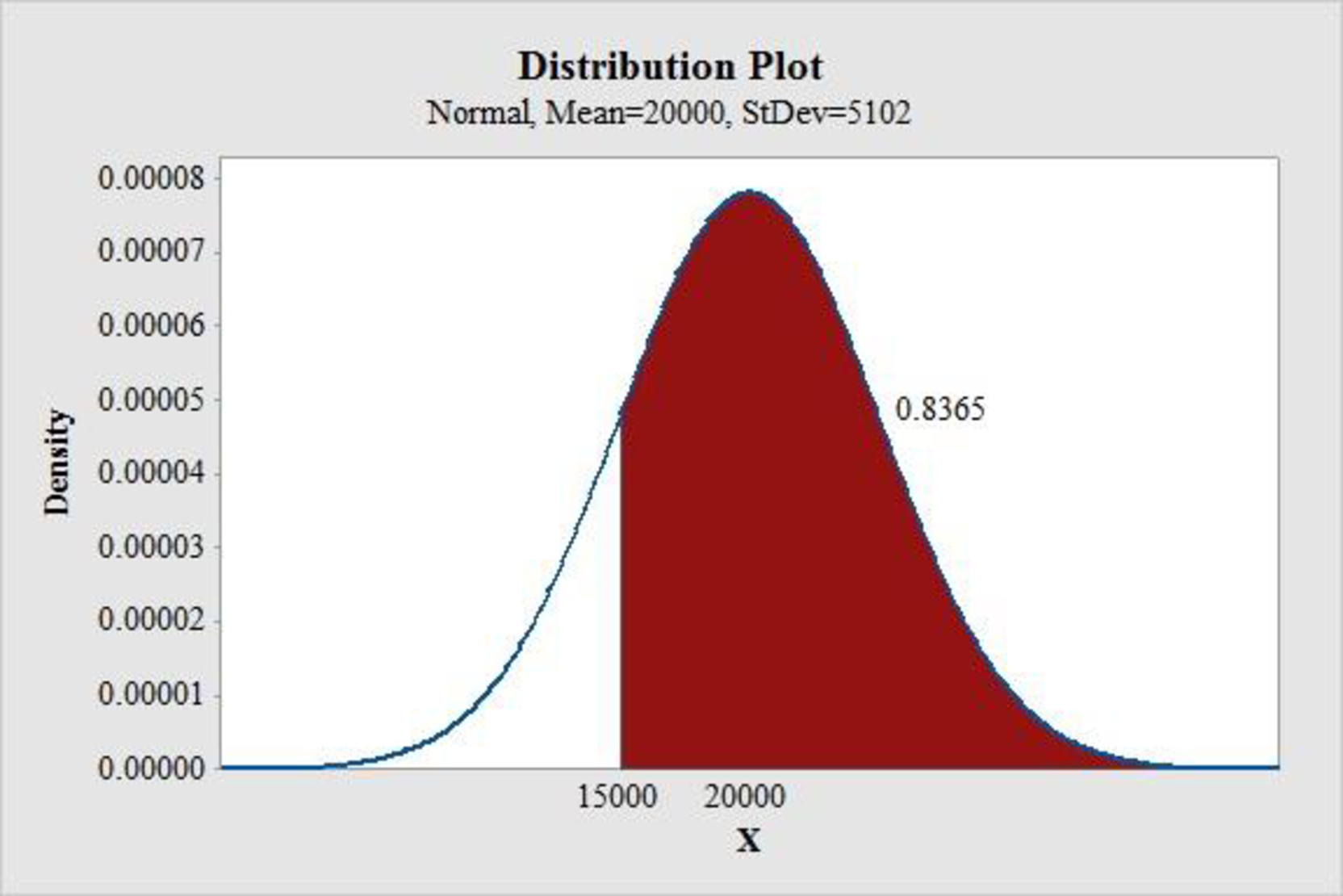
From the MINITAB output, $P\left(x>15,000\right)=0.8365$.

Thus, the probability of a stock-out for the order quantity of 15,000 units is 0.8365.

The probability of a stock-out for the order quantity of 18,000 units is $P\left(x>18,000\right)$

Software Procedure:

Step-by-step procedure to obtain the probability value using the MINITAB software:

• Choose Graph > Probability Distribution Plot
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose X Value and Right Tail for the region of the curve to shade.
• Enter the X value as 18,000.
• Click OK.

Output using the MINITAB software is given below:

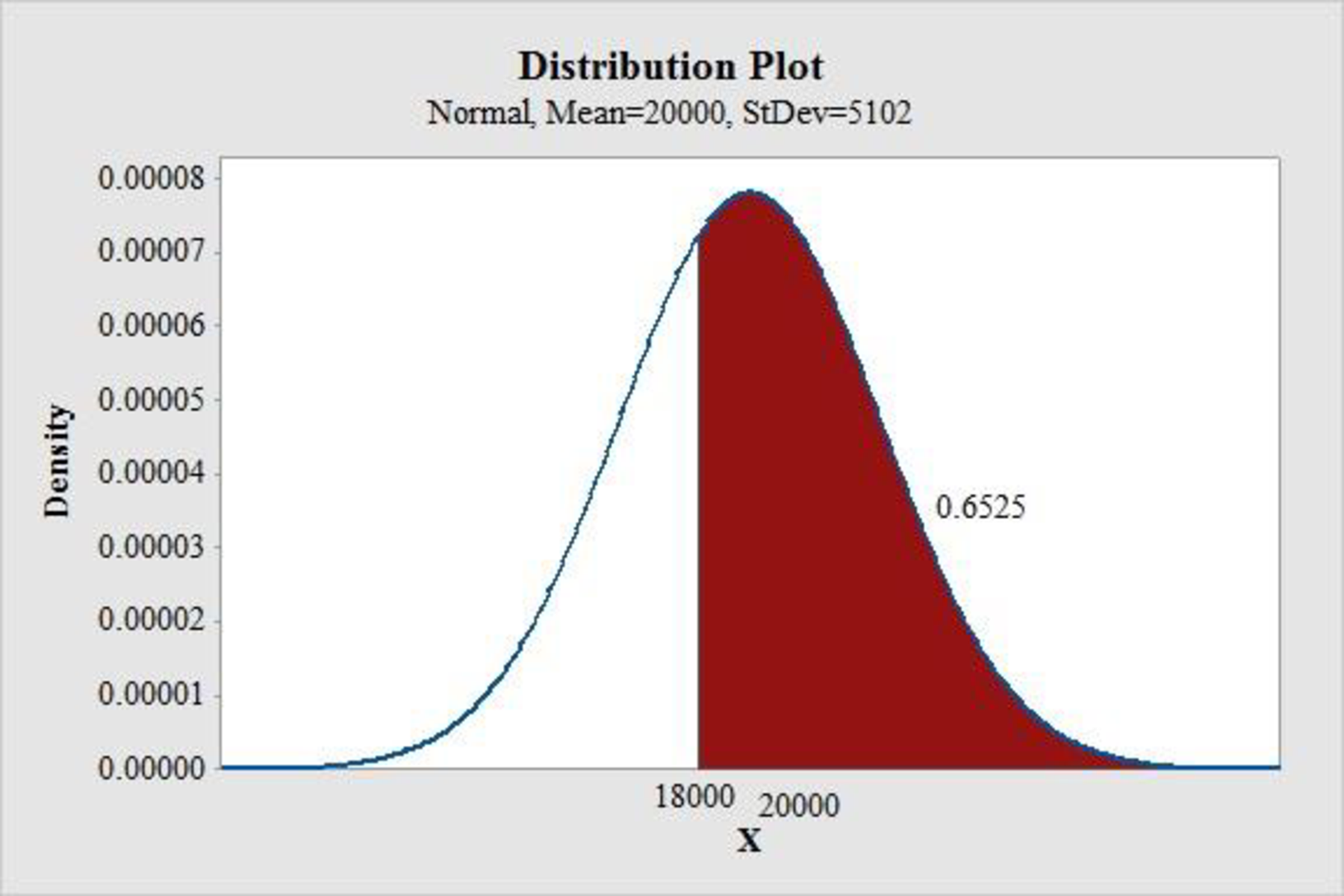
From the MINITAB output, $P\left(x>18,000\right)=0.6525$.

Thus, the probability of a stock-out for the order quantity of 18,000 units is 0.6525.

The probability of a stock-out for the order quantity of 24,000 units is $P\left(x>24,000\right)$.

Software Procedure:

Step-by-step procedure to obtain the probability value using the MINITAB software:

• Choose Graph > Probability Distribution Plot
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose X Value and Right Tail for the region of the curve to shade.
• Enter the X value as 24,000.
• Click OK.

Output using the MINITAB software is given below:

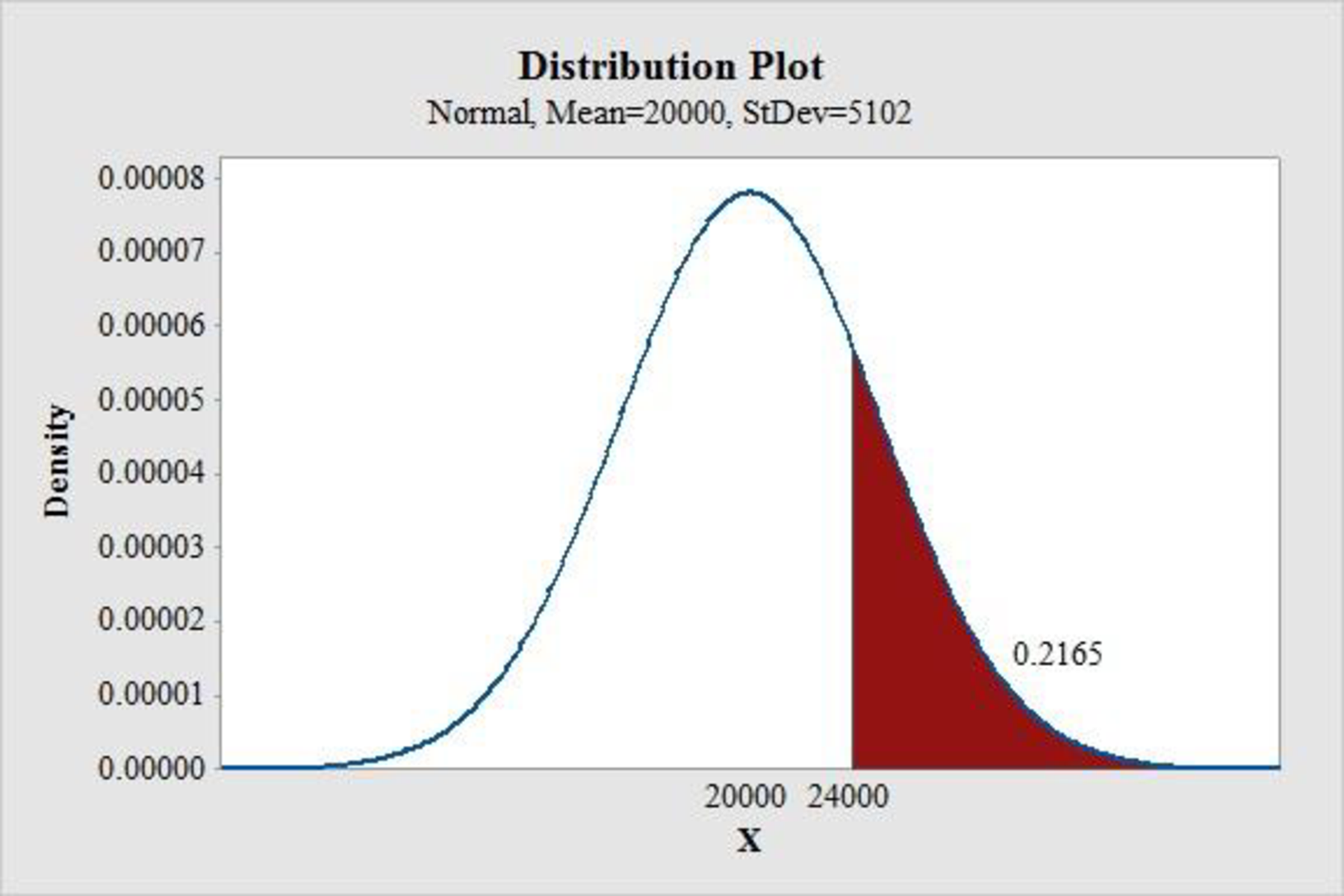
From the MINITAB output, $P\left(x>24,000\right)=0.2165$.

Thus, the probability of a stock-out for the order quantity of 24,000 units is 0.2165.

The probability of a stock-out for the order quantity of 28,000 units is $P\left(x>28,000\right)$.

Software Procedure:

Step-by-step procedure to obtain the probability value using the MINITAB software:

• Choose Graph > Probability Distribution Plot
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose X Value and Right Tail for the region of the curve to shade.
• Enter the X value as 28,000.
• Click OK.

Output using the MINITAB software is given below:

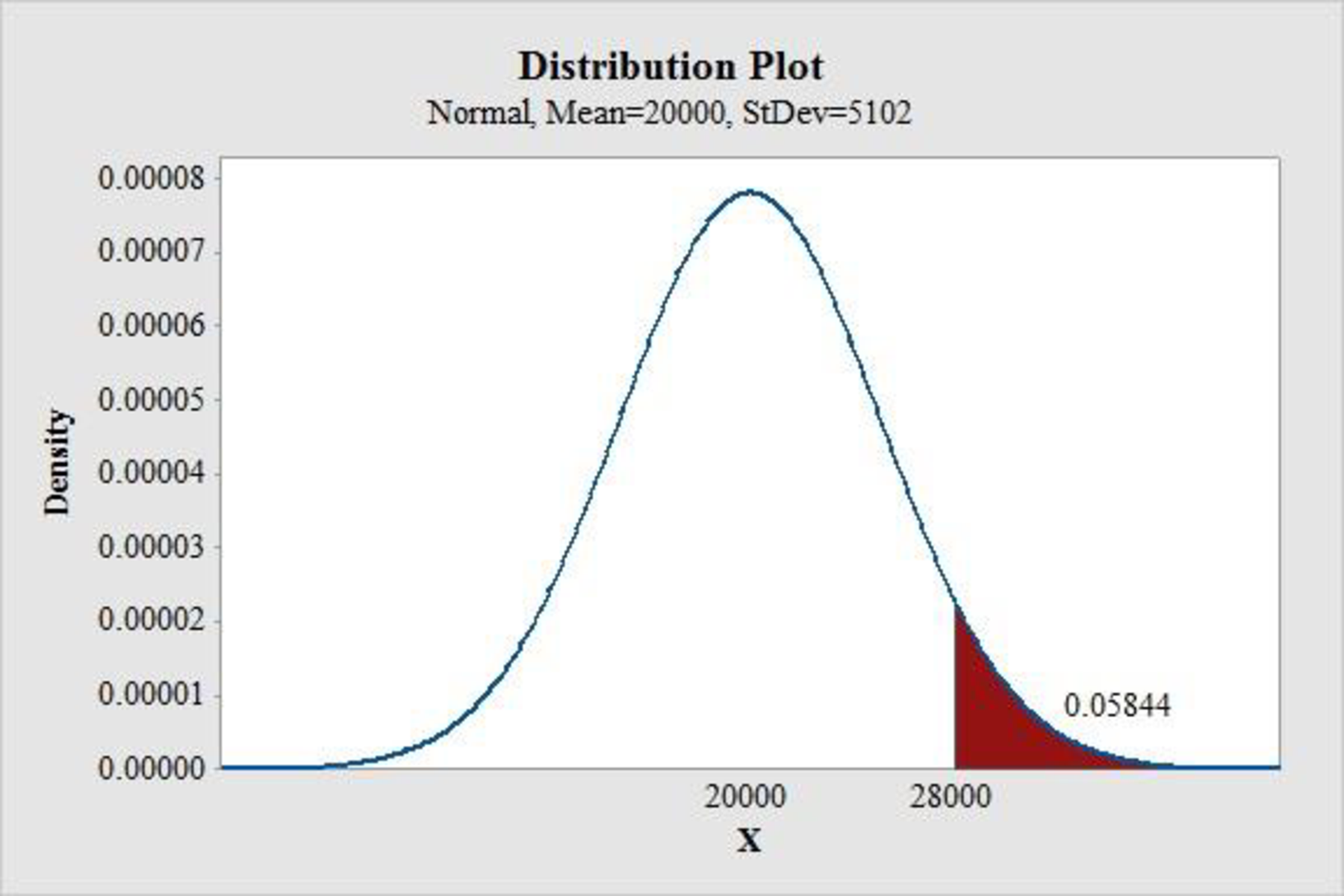
From the MINITAB output, $P\left(x>28,000\right)=0.05844$.

Thus, the probability of a stock-out for the order quantity of 28,000 units is 0.05844.

To determine

Find the projected profit for the order quantities suggested by the management team under the three scenarios.

Answer to Problem 1CP

The projected profit for the order quantities are given below:

For an order quantity of 15,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	240,000	240,000	25,000	25,000
20,000	240,000	360,000	0	120,000
30,000	240,000	360,000	0	120,000

For an order quantity of 18,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	288,000	240,000	40,000	–8,000
20,000	288,000	432,000	0	144,000
30,000	288,000	432,000	0	144,000

For an order quantity of 24,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	384,000	240,000	70,000	–74,000
20,000	384,000	480,000	20,000	116,000
30,000	384,000	576,000	0	192,000

For an order quantity of 28,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	448,000	240,000	90,000	–118,000
20,000	448,000	480,000	40,000	72,000
30,000	448,000	672,000	0	224,000

Explanation of Solution

Calculation:

The three scenarios under consideration are, worst case in which there is a sale of 10,000 units, most likely case in which there is a sale of 20,000 units and the best case in which there is a sale of 30,000 units.

The profit projections for the order quantities under three scenarios are computed using the following table:

For an order quantity of 15,000 units:

Total cost is obtained by multiplying the cost of a unit ($16) with the order quantity.

$\begin{array}{c}\text{Total cost = \$16}\times \text{Order Quantity}\\ \text{=\$16}\times \text{15,000}\\ \text{=\$240,000}\end{array}$

The income at $24 is obtained by multiplying $24 with the number of units sold.

$\begin{array}{c}\text{Income at \$24=\$24}\times \text{Number of units sold}\\ \text{=\$24}\times \text{10,000}\\ \text{=\$240,000}\end{array}$

For the unit sales more than 15, 000, the income at $24 is obtained by multiplying $24 with the order quantity 15,000 units.

$\begin{array}{c}\text{Income at \$24=\$24}\times \text{Order quantity}\\ \text{=\$24}\times \text{15,000}\\ \text{=\$360,000}\end{array}$

The income at $5 is obtained by multiplying $5 with the number of surplus units (number of units sold–order quantity).

$\begin{array}{c}\text{Income at \$5=\$5}\times \text{surplus units}\\ \text{=\$5}\times 5\text{,000}\\ \text{=\$25,000}\end{array}$

The income at $5 will be zero for the order quantities more than 15,000 units.

The profit is obtained as shown below:

$\begin{array}{c}\text{Profit}=\text{Total cost}-\text{Income}\\ \text{=Total cost}-\left(\text{Income at \$24+ Income at \$5}\right)\end{array}$

Profit obtained for a sale of 10,000 units is,

$\begin{array}{c}\text{Profit}=\text{Total cost}-\text{Income}\\ \text{=Total cost}-\left(\text{Income at \$24+ Income at \$5}\right)\\ =240,000-\left(240,000+25,000\right)\\ =25,000\end{array}$

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	240,000	240,000	25,000	25,000
20,000	240,000	360,000	0	120,000
30,000	240,000	360,000	0	120,000

Similarly, the profit projections are obtained and are given in the following tables:

For an order quantity of 18,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	288,000	240,000	40,000	–8,000
20,000	288,000	432,000	0	144,000
30,000	288,000	432,000	0	144,000

For an order quantity of 24,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	384,000	240,000	70,000	–74,000
20,000	384,000	480,000	20,000	116,000
30,000	384,000	576,000	0	192,000

For an order quantity of 28,000 units:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	448,000	240,000	90,000	–118,000
20,000	448,000	480,000	40,000	72,000
30,000	448,000	672,000	0	224,000

To determine

Find quantity that would be ordered under the policy and the profit at three sales scenarios.

Answer to Problem 1CP

The quantity that would be ordered under the policy is 22,675.

The profit at three sales scenarios are given in the following table:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	362,800	240,000	63,375	–59,425
20,000	362,800	480,000	13,375	130,575
30,000	362,800	544,200	0	181,400

Explanation of Solution

Calculation:

The order quantity should have a 70% chance of meeting demand and only a 30% chance of any stock outs. That is the order quantity that cuts off an area of 0.70 in the lower tail of the normal curve for demand.

Software Procedure:

Step-by-step procedure to obtain the x value using the MINITAB software:

• Choose Graph > Probability Distribution Plot.
• Choose View Probability > OK.
• From Distribution, choose ‘Normal’ distribution.
• Enter the Mean as 20,000 and Standard deviation as 5,102.
• Click the Shaded Area tab.
• Choose Probability Value and left tail for the region of the curve to shade.
• Enter the Probability value as 0.70.
• Click OK.

Output using the MINITAB software is given below:

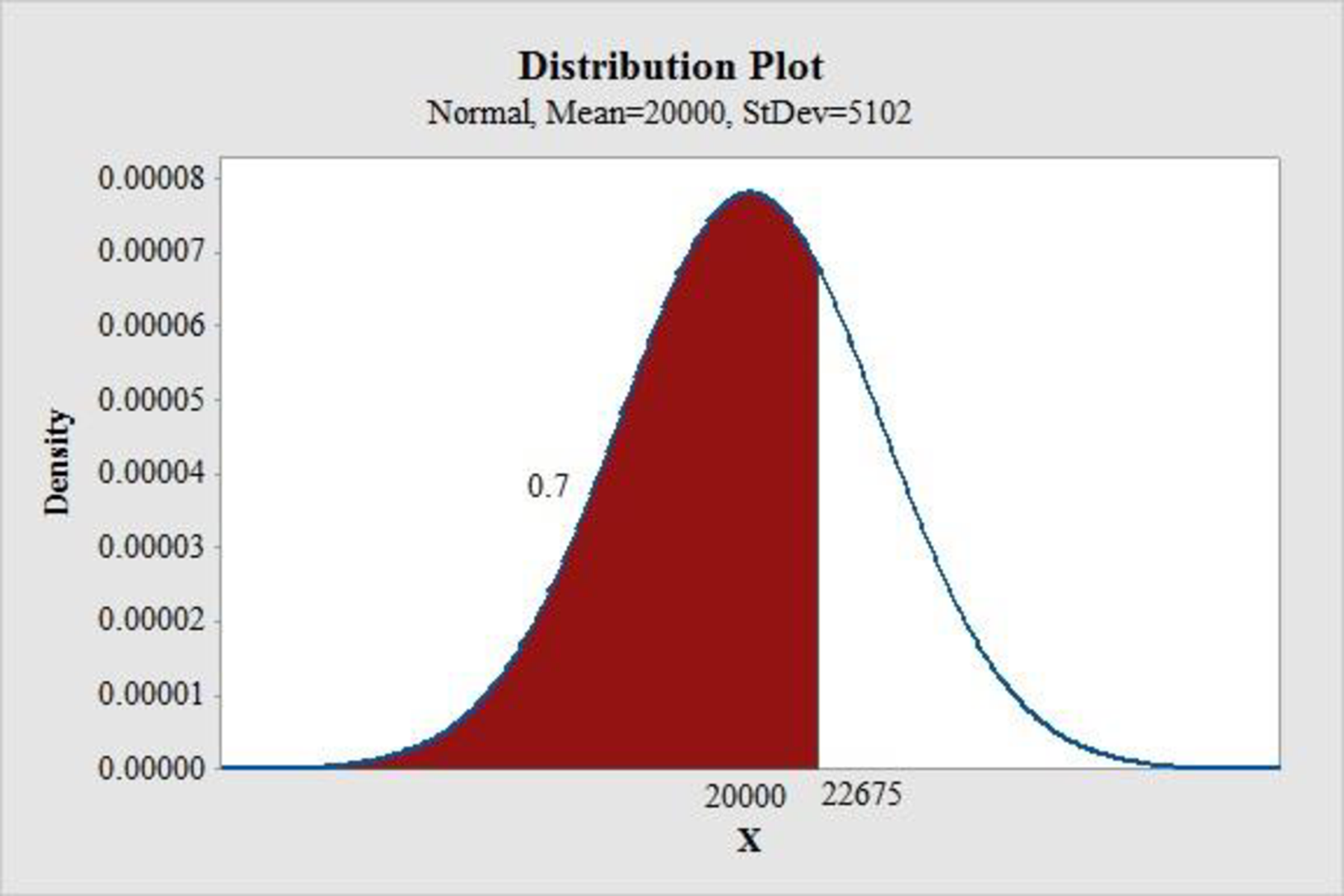
Thus, the quantity that would be ordered under the policy is 22,675.

The profit projections are obtained with the similar calculations made in part(c) for an order quantity of 22,675 units and is given in the following table:

Unit sales	Total cost ($)	At $24	At $5	Profit($)
10,000	362,800	240,000	63,375	–59,425
20,000	362,800	480,000	13,375	130,575
30,000	362,800	544,200	0	181,400

To determine

Provide the recommendation for an order quantity and note the associated profit projections and provide the rationale for the recommendation.

Explanation of Solution

A variety of recommendations are possible. From the three scenarios used in part (c) and (d) it is clear that an order quantity in the range 18,000 to 20,000 will be good to generate profit. Because the order quantities of more than 20,000 units generates a risk of loss and reduces the chance of generating good profits.