Chapter 6, Problem 100P

(a)

To determine

The amount of energy dissipated by friction.

Answer to Problem 100P

The amount of energy dissipated by friction is $\underset{\_}{935\text{J}}$.

Explanation of Solution

Figure 1 represents the free body diagram of the crate.

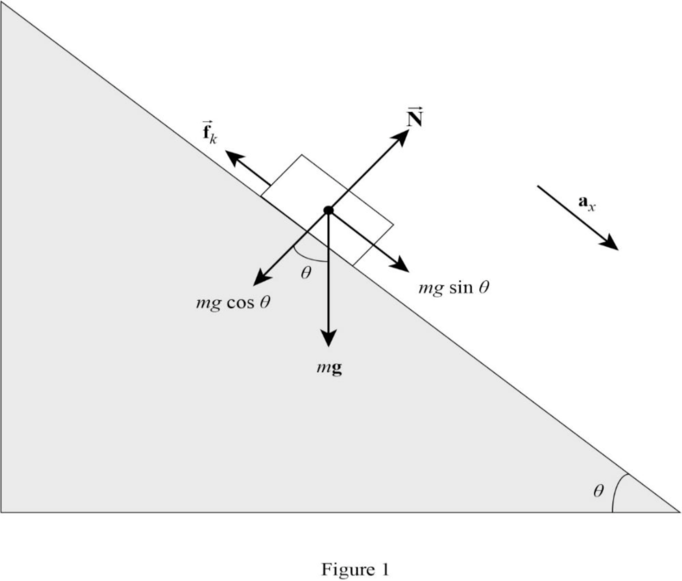
For an isolated system the total energy of the system (the sum of mechanical energy and its internal energy) is conserved.

    $\Delta K+\Delta U+\Delta E_{\text{int}}=0$

Here, $\Delta K$ is the change in kinetic energy, $\Delta U$ is the change in potential energy, and $\Delta E_{\text{int}}$ is the change in internal energy of the system.

In this situation, the work done by the frictional force is equal to the change in internal energy of the system.

The above equation is reduced to.

    $\left(\frac{1}{2}m{v}_f^2-\frac{1}{2}m{v}_i^2\right)+mg\Delta y+\Delta E_{\text{int}}=0$

Here, $\Delta E_{\text{int}}$ is the energy dissipated by friction, $m$ is the mass of the crate, $g$ is the acceleration due to gravity, and $\Delta y$ is the distance travelled along the incline.

Since the final velocity of the crate is zero and the distance travelled along incline is given by $-d\sin \theta$, the above equation is reduced to

    $-\frac{1}{2}m{v}_i^2-mgd\sin \theta +\Delta E_{\text{int}}=0$        (I)

Here, $d$ is the distance travelled along the incline.

Rearrange the above equation.

    $\Delta E_{\text{int}}=\frac{1}{2}m{v}_i^2+mgd\sin \theta$        (II)

Conclusion:

Substitute $100\text{kg}$ for $m$, $2\text{m}/\text{s}$ for $v_i$, $9.8\text{m}/{\text{s}}^2$ for $g$, $1.5\text{m}$ for $d$, and $30°$ for $\theta$ in equation (I), to find $\Delta E_{\text{int}}$.

    $\begin{array}{c}\Delta E_{\text{int}}=\frac{1}{2}\left(100\text{kg}\right){\left(2\text{m}/\text{s}\right)}^2-\left(100\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\left(1.5\text{m}\right)\sin 30°\\ =935\text{J}\end{array}$

Therefore, the amount of energy dissipated by friction is $\underset{\_}{935\text{J}}$.

(b)

To determine

The coefficient of the sliding friction.

Answer to Problem 100P

The coefficient of the sliding friction is $\underset{\_}{0.73}$.

Explanation of Solution

Write the expression for net force acting along y direction.

    ${\displaystyle \sum F_{\text{y}}=}0$

Apply the above condition in Figure 1.

    $\begin{array}{c}N-mg\cos \theta =0\\ N=mg\cos \theta \end{array}$        (III)

Write the expression for internal energy dissipated by friction.

    $\Delta E_{\text{fric}}={\mu }_{\text{k}}Nd$

Here, ${\mu }_{\text{k}}$ is the coefficient of kinetic friction, $N$ is the normal force, and $d$ is the distance travelled along the incline.

Use the above equation in equation (III).

    $\Delta E_{\text{fric}}={\mu }_{\text{k}}mg\cos \theta d$

Rearrange the above equation to find ${\mu }_{\text{k}}$.

    ${\mu }_{\text{k}}=\frac{\Delta E_{\text{fric}}}{mgd\cos \theta }$        (IV)

Conclusion:

Substitute $935\text{J}$ for $\Delta E_{\text{int}}$, $100\text{kg}$ for $m$, $9.8\text{m}/{\text{s}}^2$ for $g$, $1.5\text{m}$ for $d$, and $30°$ for $\theta$ in equation (IV), to find ${\mu }_{\text{k}}$.

    $\begin{array}{c}{\mu }_{\text{k}}=\frac{935\text{J}}{\left(100\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\left(1.5\text{m}\right)\cos 30°}\\ =0.73\end{array}$

Therefore, the coefficient of the sliding friction is $\underset{\_}{0.73}$.