
Concept explainers
You conduct a poll in which you randomly select 1000 registered voters from Texas and ask if they approve of the job their governor is doing. The population for this study is
a. all registered voters in the state of Texas.
b. the 1000 people that you interview.
c. the governor of Texas.
What is meant by Population of a study.
Answer to Problem 1QQ
Solution:
a. All registered voters in the state of Texas.
Explanation of Solution
Given:
Here in our question a poll is conducted by randomly selecting 1000 registered voters from Texas and ask if they approve of the job of their Governor is Doing.
Explanation:
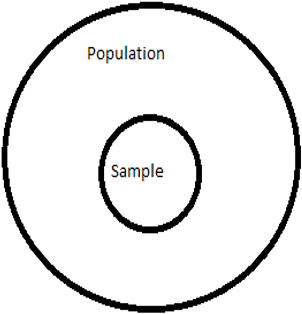
In any statistical survey we select a bunch of people from the entire pool and conduct our survey on them and we try to estimate the actual parameter. The bunch of people we select is known as Sample and the entire pool of people from which the Sample is selected is known as Population.
For Example: If I want to know who is going to win in next election for mayor in a city, I select randomly a set of people from all different streets of the city and ask them who is going to win among Mr. X and Mr. Y. So, who ever got the majority of votes from the people we selected, I conclude that person is going to win the next mayor election. So here the bunch of people selected are known as Sample and All the people who can vote in the city are known to be the Population.
Conclusion:
So here the selected 1000 registered voters from Texas whom we asked about Governor is our Sample and our Sample is selected from entire registered voters in Texas. So, all registered voters in Texas is our Population.
Want to see more full solutions like this?
Chapter 5 Solutions
EBK USING & UNDERSTANDING MATHEMATICS
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics: Picturing the World (7th Edition)
College Algebra with Modeling & Visualization (5th Edition)
- 3. f(7) 3. Find the domain of each of the following functions. 1 1. f(x)=2-6x+8 2. f(x)=√√7-x 4. A manufacturer has a monthly fixed cost of $40,000 and a production cost of $8 for each unit produced. The product sells for $12 per unit.arrow_forward7. Evaluate the following limits and justify each step. (a) lim (3x²+2x+1) 1 x²+4x-12 (b) lim 1 2 x² - 2x t-√√3t+4 (c) lim t-0 4-t x²-6x+5 (d) lim (e) lim x 5 x-5 x→2 x²+2x+3 4u+1-3 (f) lim u➡2 u-2 1 (g) lim x-3 2 x 55 x - 7x4 +4 (h) lim xx 5x+2x-1 x+1 (i) lim x²-2x+5 - 7x8+4x7 +5xarrow_forward6. Given the following graph f(x). (-2,2) 2- -5 -3 -2 (-2,-1) -1 (0,1) -2- 1 (3,0) 2 3 4 5 (3,-1) א X Compute each of the following. (a) f(-2) (b) lim f(x) #129 (c) lim f(x) *→12+ (d) lim f(x) 811H (e) f(0) (f) lim f(x) 8011 (m) Is the function continuous at x = -2,0,3? Why or why not? (g) lim f(x) +0x (h) lim f(x) x 0 (i) f(3) (j) lim f(x) x-3- (k) lim f(x) x+3+ (1) lim f(x) #13arrow_forward
- (i) For a given constant a > 0, let an investor's preference be represented by the Gaussian utility function U(w)=1-e-aw² For what range of wealth level w will the investor be non-satiated and risk-averse? Explain your answer. (ii) Give an example of a utility function that exhibits DARA and verify it. (iii) Determine the class of utility functions with relative risk aversion coefficient R(w)= w², w> 0.arrow_forward3. Compute the profit corresponding to 12,000 units. 5. A rectangular box is to have a square base and a volume of 20 ft3. The material for the base costs $0.30 per ft2, the material for the sides cost $0.10 per ft2, and the material for the top costs $0.20 per ft2. Letting a denote the length of one side of the base, find a function in the variable x giving the cost of constructing the box. 6. Given the following graph f(x).arrow_forward8. On what intervals, each function continuous? (a) f(x) = 3x11 + 4x²+1 3x²+5x-1 (b) g(x) = x²-4 X, x < 1, QTs the function f(x) continuous at = 1? Use the definition of continuity to justifyarrow_forward
- review problem please help!arrow_forwardSara (a 23 year old college graduate) is starting her first career. She met with a financial planner and has determined that she wants $1,000,000 when she retires at the age of 63. She has found an annuity that pays 4.25%, compounded quarterly. What will she need to save each month, if Sara waits 20 years to start saving? N: P/Y: I%: C/Y: PMT: FV: End or Begin $4158.98 $4,115.26 $2645.83 $6,707.40arrow_forwardSara (a 23 year old college graduate) is starting her first career. She met with a financial planner and has determined that she wants $1,000,000 when she retires at the age of 63. She has found an annuity that pays 4.25%, compounded quarterly. What will she need to save each month, if a) Sara begins saving now? N: P/Y: I%: C/Y: PMT: FV: End or Begin $1,323.80 $1,376.59 $794.74 $1,000,000arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning





