
Concept explainers
The Tautochrone. A problem of interest in the history of mathematics is that of finding the Tautochrone-the curve down which a particle will slide freely under gravity alone, reaching the bottom in the same time regardless of its starting point on the curve. This problem arose in the construction of a clock pendulum whose period is independent of the amplitude of its motion. The Tautochrone was found by Christian Huygens in
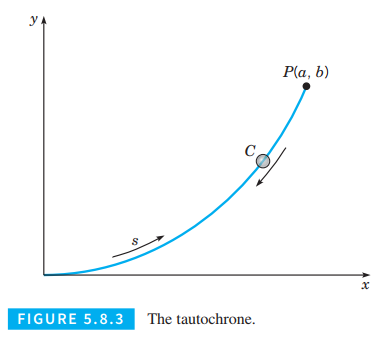
The geometric configuration is shown in Figure
Then it follows from the principle of conservation of energy that the time
(a) Assume that
Then show that
Hint: See Problem 37 of Section 5.1.
(b) Combining Eqs. (i) and (iv), show that
where
(c) Use the substitution
Equations (vi) can be identified as parametric equations of a cycloid. Thus the Tautochrone is an arc of a cycloid.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
DIFFERENTIAL EQUATIONS(LL) W/WILEYPLUS
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
Precalculus: Mathematics for Calculus (Standalone Book)
Elementary Statistics: Picturing the World (7th Edition)
Graphical Approach To College Algebra
- Calculate these limits. If the limit is ∞ or -∞, write infinity or-infinity. If the limit does not exist, write DNE: Hint: Remember the first thing you check when you are looking at a limit of a quotient is the limit value of the denominator. 1. If the denominator does not go to 0, you should be able to right down the answer immediately. 2. If the denominator goes to 0, but the numerator does not, you will have to check the sign (±) of the quotient, from both sides if the limit is not one-sided. 3. If both the numerator and the denominator go to 0, you have to do the algebraic trick of rationalizing. So, group your limits into these three forms and work with them one group at a time. (a) lim t-pi/2 sint-√ sin 2t+14cos ² t 7 2 2 2cos t (b) lim sint + sin 2t+14cos = ∞ t-pi/2 2 2cos t (c) lim cost-√sin 2t+14cos² t = t-pi/2 2cos t (d) lim t→pi/2 cost+√ sin t + 14cos 2cos ² t = ∞ (e) lim sint-v sin 2 t + 14cos = 0 t-pi/2 (f) lim t-pi/2 sin t +√ sin 2sin 2 t 2 t + 14cos t 2sin t cost- (g)…arrow_forwardThink of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector a--b geometrically?arrow_forwardGiven: AABE ~ ACDE. Prove: AC bisects BD. Note: quadrilateral properties are not permitted in this proof. Step Statement Reason AABE ACDE Given 2 ZDEC ZAEB Vertical angles are congruent try Type of Statement A E B D Carrow_forward
- 10-2 Let A = 02-4 and b = 4 Denote the columns of A by a₁, a2, a3, and let W = Span {a1, a2, a̸3}. -4 6 5 - 35 a. Is b in {a1, a2, a3}? How many vectors are in {a₁, a₂, a3}? b. Is b in W? How many vectors are in W? c. Show that a2 is in W. [Hint: Row operations are unnecessary.] a. Is b in {a₁, a2, a3}? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. ○ A. No, b is not in {a₁, a2, 3} since it cannot be generated by a linear combination of a₁, a2, and a3. B. No, b is not in (a1, a2, a3} since b is not equal to a₁, a2, or a3. C. Yes, b is in (a1, a2, a3} since b = a (Type a whole number.) D. Yes, b is in (a1, a2, 3} since, although b is not equal to a₁, a2, or a3, it can be expressed as a linear combination of them. In particular, b = + + ☐ az. (Simplify your answers.)arrow_forward(1) (14 points) Let a = (-2, 10, -4) and b = (3, 1, 1). (a) (4 points) Using the dot product determine the angle between a and b. (b) (2 points) Determine the cross product vector axb. (c) (4 points) Calculate the area of the parallelogram spanned by a and b. Justify your answer. 1arrow_forward(d) (4 points) Think of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector ab geometrically? d be .dx adjarrow_forward
- 2) Based on the given information and the diagram, a. Which congruence statements can be proven? Select all that apply.Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: angle 3 is congruent to angle 5A. Overline ON is congruent to overline OPB. Angle 1 is congruent to angle 2C. Overline ON is congruent to overline OR and overline OP is congruent to overine OQD. angle 1 is congruent to angle 3 and angle 2 is congruent to angle 5There are more than one correct answerarrow_forward(2) (4 points) Find all vectors v having length 1 that are perpendicular to both =(2,0,2) and j = (0,1,0). Show all work. a=arrow_forwardNo chatgpt pls will upvotearrow_forward
- Title: Analyzing Customer Satisfaction for UnileverAs a member of Unilever's Customer Experience Management team, you are responsible forevaluating customer satisfaction levels and monitoring competitive moves. This case studyinvolves analyzing satisfaction data to test two key hypotheses about Unilever's performancerelative to its main competitor, Procter & Gamble (P&G).Unilever’s leadership team has emphasized the importance of customer satisfaction inmaintaining competitive advantage and market leadership. As part of this initiative, yourteam regularly monitors satisfaction scores and benchmarks them against competitors likeP&G.You are tasked with analyzing the provided dataset to answer the following questions:1. Does Unilever’s average customer satisfaction score meet the minimum threshold of2. 75%?Is there no significant difference between Unilever’s overall average satisfaction scoreand P&G’s average satisfaction score?arrow_forwardPlease help me first one graphically and the other in matrixarrow_forwardPlease help me with this in matrix pleasearrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning  Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning




