Calculus Volume 3
Calculus Volume 3
16th Edition
ISBN: 9781938168079
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
bartleby

Concept explainers

Arc Length
Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Arc length is used in a wide range of real applications. We might be interested in knowing how far a rocket travels if it is launched along a parabolic…
Line Integral
A line integral is one of the important topics that are discussed in the calculus syllabus. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Evaluation of a function along…
Triple Integral
Examples:
bartleby

Videos

Textbook Question
Book Icon
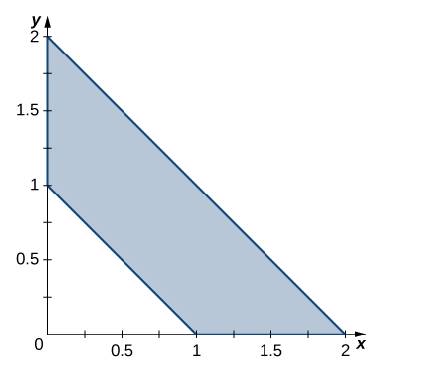Chapter 5.7, Problem 397E

In the following exercises, use the transformation u = x + y. V = x — y to evaluate the integrals on the trapezoidal region R determined by the points (1, 0). (2. 0). (0. 2). and (0. 1) shown in the following figure.

Chapter 5.7, Problem 397E, In the following exercises, use the transformation u = x + y. V = x — y to evaluate the integrals on 397. ∬ R ( x 2 − 2 x y + y 2 ) e x + y d A

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 5.7, Problem 396E
Next
Chapter 5.7, Problem 398E
Students have asked these similar questions
Solve no chatgpt already got wrong chatgpt answer
Not use ai please
You may need to use the appropriate appendix table or technology to answer this question. You are given the following information obtained from a random sample of 4 observations. 24 48 31 57 You want to determine whether or not the mean of the population from which this sample was taken is significantly different from 49. (Assume the population is normally distributed.) (a) State the null and the alternative hypotheses. (Enter != for ≠ as needed.) H0:     Ha:     (b) Determine the test statistic. (Round your answer to three decimal places.)   (c) Determine the p-value, and at the 5% level of significance, test to determine whether or not the mean of the population is significantly different from 49. Find the p-value. (Round your answer to four decimal places.) p-value = State your conclusion. Reject H0. There is insufficient evidence to conclude that the mean of the population is different from 49.Do not reject H0. There is sufficient evidence to conclude that the…

Chapter 5 Solutions

Calculus Volume 3

Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...
Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - function over the given rectangles. 35....Ch. 5.1 - function over the given rectangles. 36....Ch. 5.1 - function over the given rectangles. 37....Ch. 5.1 - function over the given rectangles. 38....Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - [T] Consider the function f(x,y)=ex2y2where...Ch. 5.1 - [T] Consider the function f(x,y)=sin(x2)cos(y2) ....Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - An isotherm map is a chart connecting points...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - wIn the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - Evaluate the iterated integrals. 80. 012x3x(x+ y...Ch. 5.2 - Evaluate the iterated integrals. 81....Ch. 5.2 - Evaluate the iterated integrals. 82....Ch. 5.2 - Evaluate the iterated integrals. 83....Ch. 5.2 - Evaluate the iterated integrals. 84. 01 1 y 2 1 y...Ch. 5.2 - Evaluate the iterated integrals. 85. 01/2 14 y 2...Ch. 5.2 - Evaluate the iterated integrals. 86. Let D be the...Ch. 5.2 - Evaluate the iterated integrals. 87. Let D be the...Ch. 5.2 - yEvaluate the iterated integrals. 88. a. Show that...Ch. 5.2 - Evaluate the iterated integrals. 89. a. Show that...Ch. 5.2 - The region D bounded by x=0,y=x5+1 , and S y=3x2...Ch. 5.2 - The legion D bounded by y = cos x. y = 4 cos x....Ch. 5.2 - Find the area A(D) of the region...Ch. 5.2 - Let D be the region bounded by y = 1, y = x. y =...Ch. 5.2 - Find the average value of the function f(x. y) =...Ch. 5.2 - Find the average value of the function f(x. y) =-x...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - The region D is shown in the following figure....Ch. 5.2 - The region D is given in the following figure....Ch. 5.2 - Find the volume of the solid under the surface...Ch. 5.2 - Find the volume of the solid tinder the plane...Ch. 5.2 - Find the volume of the solid tinder the plane z=xy...Ch. 5.2 - Find the volume of the solid under the surface z =...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Let S1 and S2 , be the solids situated in the...Ch. 5.2 - Let S and 5, be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - [T] The following figure shows the region D...Ch. 5.2 - [T] The region D bounded by the curves y=cosx,x=0...Ch. 5.2 - Suppose that (X. Y) is the outcome of an...Ch. 5.2 - Consider X and Y two random variables of...Ch. 5.2 - [T] The Reuleaux triangle consists of an...Ch. 5.2 - [T] Show that the area of the lunes of Alhazen,...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - Evaluate the integral DffrdAwhere D is the region...Ch. 5.3 - Find the area of the region D bounded by the polar...Ch. 5.3 - Evaluate the integral DrdA, where D is the region...Ch. 5.3 - Find the total area of the region enclosed by the...Ch. 5.3 - Find the area of the region D, which is the region...Ch. 5.3 - Find the area of the region D. which is the region...Ch. 5.3 - Determine the average value of the function f(x....Ch. 5.3 - Determine the average value of the function...Ch. 5.3 - Find the volume of the solid situated in the first...Ch. 5.3 - Find the volume of the solid bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 inside the unit...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - Find the volume of the solid that lies tinder the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - A radial function f is a function whose value at...Ch. 5.3 - Use the information from the preceding exercise to...Ch. 5.3 - Let f(x,y)=F(r)rbe a continuous radial function...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Evaluate Dff arctan (yx)x2+y2dA. where...Ch. 5.3 - A spherical cap is the region of a sphere that...Ch. 5.3 - In statistics, the joint density for two...Ch. 5.3 - The double improper integral e( x2 +y 2/2 )dxdymay...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - Let F. G and H be continuous functions on [a,b]...Ch. 5.4 - Let F. G. and H be differential functions on...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - The solid E bounded by y2+z2=9,x=0 . x = 5 is...Ch. 5.4 - The solid E bounded by y=x,x=4,y=0 , and z = 1 is...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Find the average value of the function f(x. y, z)...Ch. 5.4 - Find the average value of the function...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Consider the pyramid with the base in the xv...Ch. 5.4 - Consider the pyramid with the base in the xy...Ch. 5.4 - The solid E bounded by the sphere of equation...Ch. 5.4 - The solid E bounded by the equation 9x2+4y2+z2=1...Ch. 5.4 - Find the volume of the prism with vertices (0, 0....Ch. 5.4 - Find the volume of the prism with vertices (0. 0....Ch. 5.4 - The solid E bounded by z= 10—2x—y and situated in...Ch. 5.4 - The solid E bounded by z=1x2 and situated in the...Ch. 5.4 - The midpoint rule for the triple integral...Ch. 5.4 - [T] a. Apply the midpoint rule to approximate...Ch. 5.4 - Suppose that the temperature in degrees Celsius at...Ch. 5.4 - Suppose that the temperature in degrees Fahrenheit...Ch. 5.4 - Show that the volume of a right square pyramid of...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - If the charge density at an arbitraiy point (x, y....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - [T] Use a computer algebra system (CAS) to graph...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - 267. Convert the integral into an integral in...Ch. 5.5 - Convert the integral 020x 01 ( xy+z) dzdxdy into...Ch. 5.5 - f(x,y,z)=1,B={(x,y,z)x2+y2+z290,z0}Ch. 5.5 - 270. f(x,y,z)=1x2+y2+z2,B={(x,y,z)x2+y2+z29,y0,z0}Ch. 5.5 - f(x,y,z)=x2+y2. B is bounded above by the...Ch. 5.5 - f(x. y, z) = z. B is bounded above by the half...Ch. 5.5 - Show that if F(,,)=f()g()h() is a continuous...Ch. 5.5 - a. A function F is said to have spherical svmmetiy...Ch. 5.5 - a. Let B be the region between the upper...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Convert the integral f44f16 y 216y2f16 x 2 y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to evaluate the integral...Ch. 5.5 - [T] a. Evaluate the integral Ee x 2 + y 2 + z 2...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - The power emitted by an antenna has a power...Ch. 5.5 - Use the preceding exercise to find the total power...Ch. 5.5 - A charge cloud contained in a sphere B of radius r...Ch. 5.5 - Use the preceding exercise to find the total...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - Let Q be the solid unit cube. Find the mass of the...Ch. 5.6 - Let Q be the solid unit hemisphere. Find the mass...Ch. 5.6 - The solid Q of constant density I is situated...Ch. 5.6 - Find the mass of the solid...Ch. 5.6 - Consider the solid Q={(x,y,z)0x1,0y2,0z3} with the...Ch. 5.6 - [T] The solid Q has the mass given by the triple N...Ch. 5.6 - The solid Q is bounded by the planes...Ch. 5.6 - The solid Q is bounded by the planes x+y+z=3 . and...Ch. 5.6 - Let Q be the solid situated outside the sphere...Ch. 5.6 - The mass of a solid is given by 0f20f4x2 x 2+ y...Ch. 5.6 - Let Q be the solid bounded above the cone x2+y2=z2...Ch. 5.6 - The solid Q={(x,y,z)0x2+y216,x0,y0,0zx} has the...Ch. 5.6 - The solid Q is bounded by the cylinder + = a2. the...Ch. 5.6 - Let Q be a solid of constant density k. where k >...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - The solid Q has the moment of inertia Ixabout...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - A solid Q has a volume given by DabdAdz. where D...Ch. 5.6 - Consider the solid enclosed by the cylinder...Ch. 5.6 - [T] The average density of a solid Q is defined as...Ch. 5.6 - Show that the moments of inertia Ix,Iy. and...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - The triangular region R with the vertices...Ch. 5.7 - The triangular region R with the vertices (0, 0)....Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - The circular annulus sector R bounded by the...Ch. 5.7 - The solid R bounded by the circular cylinder...Ch. 5.7 - Show that Rf( x 2 3 + y 2 3 )dA=21501f()dp. where...Ch. 5.7 - Show that Rf( 16 x 2 +4y+ x 2 )dv=201f()2dp. where...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - A transformation T:R2R2,T(u,v)=(x,y)of the form x...Ch. 5.7 - The transformation T:R2T(u,v)=(x,y) . where...Ch. 5.7 - [T] Find the region S in the uv-plane whose image...Ch. 5.7 - [T] The transformations T : R P. i = 1,.... 4....Ch. 5.7 - [T] The transformation...Ch. 5.7 - [T] Find transformations...Ch. 5.7 - Use the transformation, x=au,y=av,z=cw and...Ch. 5.7 - Find the volume of a football whose shape is a...Ch. 5.7 - [T] Lamé ovals (or superellipses) are plane curves...Ch. 5.7 - [T] Lamé ovals have been consistently used by...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems consider the temperature...Ch. 5 - [T] The density of Earth’s layers is displayed in...Ch. 5 - The following problems concern the Theorem of...Ch. 5 - The following problems concern the Theorem of...

Additional Math Textbook Solutions

Find more solutions based on key concepts
TRY IT YOURSELF 1 Find the mean of the points scored by the 51 winning teams listed on page 39.

Elementary Statistics: Picturing the World (7th Edition)

CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.

Thinking Mathematically (6th Edition)

Critical Thinking. For Exercises 5-20, watch out for these little buggers. Each of these exercises involves som...

Elementary Statistics (13th Edition)

Version 2 of the Chain Rule Use Version 2 of the Chain Rule to calculate the derivatives of the following funct...

Calculus: Early Transcendentals (2nd Edition)

In Problems 19-30, state the domain and range for each relation. Then determine whether each relation represent...

Precalculus

Assessment 1-1A Cookies are sold singly or in packages of 2 or 6. With this packaging, how many ways can you bu...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Text book image
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Text book image
Calculus Volume 1
Math
ISBN:9781938168024
Author:Strang, Gilbert
Publisher:OpenStax College
Text book image
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Text book image
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY