Concept explainers
Videos
Solve the following exercises based on Principles 11-14, although an exercise may require the application of two or more of any of the principles. Round the answers to 3 decimal places where necessary unless otherwise stated.
a. If
b If
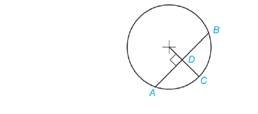
(a)
The value of DB and arc
Answer to Problem 20A
The value of DB is
Explanation of Solution
Given information:
AB = 5.378"
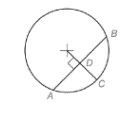
If the radius of the circle is perpendicular to the chord, it always divides the chord in two equal parts.
In the figure given above, the radius is perpendicular to the chord; hence, the parts AD will be equal to DB. Each portion AD and DB is half the value of part AB.
The value of DB is
If the radius of the circle is perpendicular to the chord, it always divides the chord and the arc cut off by the chord in two equal parts.
In the figure given above, the radius is perpendicular to the chord; hence, the parts AD will be equal to DB. Each portion AD and DB is half the value of part AB. Also, the arc cut off by the chord is divided in two equal parts.
The value of DB is
Conclusion:
Thus, the value of DB is
(b)
The value of AB and arc
Answer to Problem 20A
The value of AB is
Explanation of Solution
Given information:
AB = 3.017"
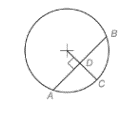
If the radius of the circle is perpendicular to the chord, it always divides the chord in two equal parts.
In the figure given above, the radius is perpendicular to the chord; hence, the parts AD will be equal to DB. Each portion AD and DB is half the value of part AB.
The value of AB is
If the radius of the circle is perpendicular to the chord, it always divides the chord and the arc cut off by the chord in two equal parts.
In the figure given above, the radius is perpendicular to the chord; hence, the parts AD will be equal to DB. Each portion AD and DB is half the value of part AB. Also, the arc cut off by the chord is divided in two equal parts.
The value of AB is
Conclusion:
Thus, the value of AB is
Want to see more full solutions like this?
Chapter 55 Solutions
Mathematics For Machine Technology
- Golden Ratio search Method f(x) = 2x^3 - 3x^2 - 12x + 1 Golden ratio search rules 1.If f(x) < f(x2): 1. Eliminate all x values less than x2 2. X2 becomes the new a 3. x, becomes the new x2 4. no change in b If f(x) > f(x2): 1. Eliminate all x values greater than x 2. x, becomes the new b 3. x2 becomes the new x 4. no change in aquesion=Narrow the interval in which the minimizer of the function f is located using the golden search method, starting with the initial interval (0,6], until its width is less than 2. Then, accept the midpoint of this interval as an approximate value of the minimizer of the function fand determine it. (ф=0.62)According to the question above, fill in the table below using the algorithm until the appropriate place.please write every step by step in a verry comprehensive wayarrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forwardFor all integers a and b, (a + b)^4 ≡ a^4 + b^4 (mod 4).arrow_forward
- Let Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forwardProve that (1) Σσς (α) μ(η/α) = n d/n (ii) Σσς(d) = η Σσο(α)/d d❘n d❘n (iii) σ (d) σ (n/d) = Σ d³oo(d) σo(n/d). d|n dnarrow_forwardhow to do part b,carrow_forward
- If p = 5 (mod 8), where p is prime, show that p|2 (P-1)/2 + 1. State and prove the corresponding result when p = 7 (mod 8). Deduce that 250 + 1 and 251 1 are composite. -arrow_forwardWhy the character no change for my remark?arrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forward
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage LearningMathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage