
Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 55, Problem 1A
Determine the length of a. Round the answer to 1 decimal place.
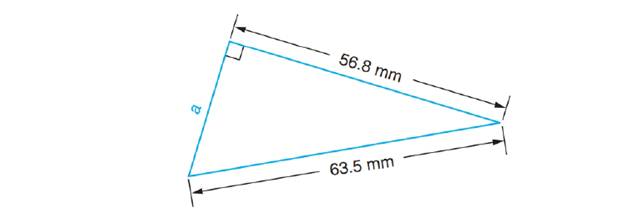
Expert Solution & Answer
To determine
The length of side a of the given triangle.
Answer to Problem 1A
The length of side a is
Explanation of Solution
Given:
The following figure is given.
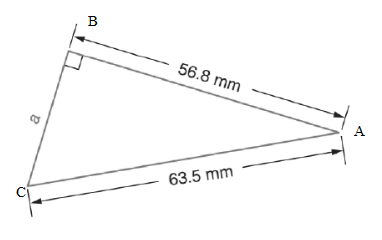
If one of the angles of any triangle is denoted by a rectangle, the angle is considered as a right angle. In the figure above, the angle B is the right angle and triangle ABC is the right-angle triangle.
To calculate the side BC, let us apply the Pythagoras theorem. According to Pythagoras theorem,
The length a of the given triangle is
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
7. The demand for a product, in dollars, is
p = D(x) = 1000 -0.5 -0.0002x²
1
Find the consumer surplus when the sales level is 200.
[Hints: Let pm be the market price when xm units of product are sold. Then the consumer
surplus can be calculated by foam (D(x) — pm) dx]
4. Find the general solution and the definite solution for the following differential equations:
(a)
+10y=15, y(0) = 0;
(b) 2 + 4y = 6, y(0) =
5. Find the solution to each of the following by using an appropriate formula developed in the
lecture slides:
(a) + 3y = 2, y(0) = 4;
(b) dy - 7y = 7, y(0) = 7;
(c) 3d+6y= 5, y(0) = 0
Chapter 55 Solutions
Mathematics For Machine Technology
Ch. 55 - Determine the length of a. Round the answer to 1...Ch. 55 - Prob. 2ACh. 55 - Prob. 3ACh. 55 - Prob. 4ACh. 55 - Prob. 5ACh. 55 - Prob. 6ACh. 55 - Name each of the parts of circles for the...Ch. 55 - Name each of the parts of circles for the...Ch. 55 - Name each of the parts of circles for the...Ch. 55 - Name each of the parts of circles for the...
Ch. 55 - Prob. 11ACh. 55 - Circumference Formula Use C= or C=2r where C=...Ch. 55 - Prob. 13ACh. 55 - Circumference Formula Use C= or C=2r where C=...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Prob. 17ACh. 55 - Solve the following exercises based on Principles...Ch. 55 - Prob. 19ACh. 55 - Solve the following exercises based on Principles...Ch. 55 - Prob. 21ACh. 55 - Solve the following exercises based on Principles...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Prob. 25ACh. 55 - Prob. 26ACh. 55 - Prob. 27ACh. 55 - Solve the following exercises based on Principles...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Solve the following exercises based on Principles...Ch. 55 - Prob. 31ACh. 55 - Solve the following exercises based on Principles...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 1. Evaluate the following improper integrals: (a) fe-rt dt; (b) fert dt; (c) fi da dxarrow_forward8. Given the rate of net investment I(t) = 9t¹/2, find the level of capital formation in (i) 16 years and (ii) between the 4th and the 8th years.arrow_forward9. If the marginal revenue function of a firm in the production of output is MR = 40 - 10q² where q is the level of output, and total revenue is 120 at 3 units of output, find the total revenue function. [Hints: TR = √ MRdq]arrow_forward
- 6. Solve the following first-order linear differential equations; if an initial condition is given, definitize the arbitrary constant: (a) 2 + 12y + 2et = 0, y(0) = /; (b) dy+y=tarrow_forward4. Let A = {a, b, c, d, e, f}, B = {e, f, g, h} and C = {a, e, h,i}. Let U = {a, b, c, d, e, f, g, h, i, j, k}. • Draw a Venn Diagram to describe the relationships between these sets Find (AB) NC • Find (AC) UB Find AUBUC • Find (BC) N (A - C)arrow_forward7. A consumer lives on an island where she produces two goods x and y according to the production possibility frontier x² + y² < 200 and she consumes all the goods. Her utility function is U(x, y) = x y³. She faces an environmental constraint on her total output of both goods. The environmental constraint is given by x + y ≤20. • (a) Write down the consumer's optimization problem. (b) Write out the Kuhn-Tucker first order conditions. (c) Find the consumer's optimal consumption bundle (x*, y*).arrow_forward
- 3. Answer the following questions: (a) Given the marginal propensity to import M'(Y) = 0.1 and the information that M = 20 when Y = 0, find the import function M(Y). (b) Given a continuous income stream at the constant rate of $1,000 per year, what will be the present value II if the income stream terminates after exactly 3 years and the discount rate is 0.04? (c) What is the present value of a perpetual cash flow of $2,460 per year, discounted at r = 8%?arrow_forward5. Let A and B be arbitrary sets. Prove AnB = AUB.arrow_forward2. Answer the following questions: (a) Given the marginal-revenue function R'(Q) = 28Q - €0.3Q, find the total-revenue function R(Q). What initial condition can you introduce to definitize the constant of integration? = (b) Given the marginal propensity to consume C'(Y) 0.80.1Y-1/2 and the information that C = Y when Y = 100, find the consumption function C(Y).arrow_forward
- 7. Let X, A, and B be arbitrary sets such that ACX and BC X. Prove AUB CX.arrow_forward1. Write out the following sets as a list of elements. If necessary you may use ... in your description. {x EZ: |x|< 10 A x < 0} {x ЄN: x ≤ 20 A x = 2y for some y = N} {n EN: 3 | n^ 1 < n < 20} {y Є Z: y² <0}arrow_forward3. For each statement below, write an equivalent statement using the justification given. = y Є A or yЄ B by the definition of union = y Є A or y Є B by the definition of set complement = x = C and x & D by DeMorgan's Law =Vx (x EnFxЄEUF) by definition of subset. = (X CYUZ)A (YUZ CX) by definition of set equalityarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill


Algebra - Pythagorean Theorem; Author: yaymath;https://www.youtube.com/watch?v=D_y_owf1WsI;License: Standard YouTube License, CC-BY
The Organic Chemistry Tutor; Author: Pythagorean Theorem Explained!;https://www.youtube.com/watch?v=B0G35RkmwSw;License: Standard Youtube License