Chapter 5.4, Problem 5.134P

To determine

The centroid of the section.

Answer to Problem 5.134P

The centroid of the section $\left(\overline{x},\overline{y},\overline{z}\right)$ is $\left(0,\frac{5}{16}h,-\frac{1}{4}h\right)$.

Explanation of Solution

Refer Figure 1 and Figure 2.

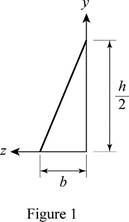
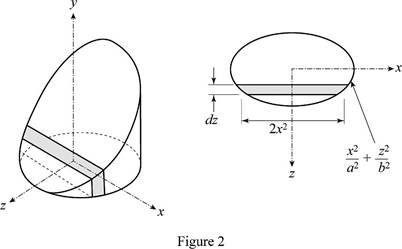
Consider an elemental section of the given section.

Write an expression to calculate the volume of the element.

$dV=2xydz$ (I)

Here, $dz$ is the thickness of the element, $dV$ is the volume of the element, $y$ is the height of the element and $x$ is the width of the element.

From the symmetry, write an expression to calculate the distance of centroid of the section from x-axis.

$\overline{x}=0$ (II)

Here, $\overline{x}$ is the distance of centroid of section from x axis.

From the symmetry, write an expression to calculate the distance of centroid of the section from x-axis.

$\overline{x}=0$ (II)

Here, $\overline{x}$ is the distance of centroid of section from x axis.

Write an expression to calculate the distance of centroid of element from z-axis.

${\overline{z}}_{EL}=z$ (IV)

Here, ${\overline{z}}_{EL}$ is the distance of centroid of element from z axis.

Write an expression to calculate width of the element.

$x=\frac{a}{b}\sqrt{b^2-z^2}$ (V)

Here, $a$ is the semi major axis of the elliptical plane and $b$ is the semi minor axis of the elliptical plane.

Write an expression to calculate the height of the element.

$\begin{array}{c}y=-\frac{\left(h/2\right)}{b}z+\frac{h}{2}\\ =\left(\frac{h}{2b}\right)\left(b-z\right)\end{array}$ (VI)

Here, $h$ is the height of the element.

Write an expression to calculate the volume of the section.

$V={\displaystyle \int 2xydz}$ (VII)

Write an expression to calculate the thickness of the section.

$z=b\sin \theta$ (VIII)

Differentiate the equation to calculate the thickness of the element.

$dz=b\cos \theta d\theta$ (IX)

Write an expression to find the distance of the centroid of the section from x axis.

$\overline{x}=\frac{{\displaystyle \int {\overline{x}}_{EL}dV}}{V}$ (X)

Here, $\overline{x}$ is the distance of centroid of section from x axis.

Write an expression to find the distance of the centroid of the section from x axis.

$\overline{y}=\frac{{\displaystyle \int {\overline{y}}_{EL}dV}}{V}$ (XI)

Here, $\overline{y}$ is the distance of centroid of section from y axis.

Write an expression to find the distance of the centroid of the section from z axis.

$\overline{z}=\frac{{\displaystyle \int {\overline{z}}_{EL}dV}}{V}$ (XII)

Here, $\overline{z}$ is the distance of centroid of section from z axis.

Conclusion:

Substitute (V), (VI) and (IX) in equation (VII) to find $V$.

$\begin{array}{c}V={\displaystyle {\int }_{-b}^b\left(2\frac{a}{b}\sqrt{b^2-z^2}\right)\left(\left(\frac{h}{2b}\right)\left(b-z\right)\right)dz}\\ =\frac{ah}{b^2}{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left(b\cos \theta \right)\left(b\left(1-\sin \theta \right)\right)b\cos \theta d\theta }\\ =abh{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left({\cos }^2\theta -\sin \theta {\cos }^2\theta \right)d\theta }\\ ={abh\left(\frac{\theta }{2}+\frac{\sin 2\theta }{4}+\frac{1}{3}{\cos }^3\theta \right)|}_{-\pi /2}^{\pi /2}\\ =\frac{1}{2}\pi abh\end{array}$ (XIII)

write an expression to calculate the distance of centroid of the element from x-axis.

$\overline{x}=0$

Write an expression to calculate ${\displaystyle \int {\overline{y}}_{EL}dV}$.

$\begin{array}{c}{\displaystyle \int {\overline{y}}_{EL}dV}={\displaystyle {\int }_{-b}^b\left(\frac{1}{2}\left(\frac{h}{2b}\right)\left(b-z\right)\right)\left(\left(2\frac{a}{b}\sqrt{b^2-z^2}\right)\left(\left(\frac{h}{2b}\right)\left(b-z\right)\right)dz\right)}\\ =\frac{1}{4}\frac{a{h}^2}{b^3}{\displaystyle {\int }_{-b}^b{\left(b-z\right)}^2\sqrt{b^2-z^2}dz}\\ =\frac{1}{4}\frac{a{h}^2}{b^3}{\displaystyle {\int }_{-\pi /2}^{\pi /2}{\left(b-b\sin \theta \right)}^2\sqrt{b^2-{\left(b\sin \theta \right)}^2}\left(b\cos \theta d\theta \right)}\\ =\frac{1}{4}\frac{a{h}^2}{b^3}{{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left(b\left(1-\sin \theta \right)\right)}}^2\left(b\cos \theta \right)\left(b\cos \theta d\theta \right)\\ =\frac{1}{4}ab{h}^2{\displaystyle {\int }_{-\pi /2}^{\pi /2}{\cos }^2\theta -2\sin \theta {\cos }^2\theta +{\sin }^2\theta {\cos }^2\theta d\theta }\\ =\frac{1}{4}ab{h}^2{\displaystyle {\int }_{-\pi /2}^{\pi /2}{\cos }^2\theta -2\sin \theta {\cos }^2\theta +\left(\frac{1}{2}\left(1-\cos 2\theta \right)\right)\left(\frac{1}{2}\left(1+\cos 2\theta \right)\right)d\theta }\\ =\frac{1}{4}ab{h}^2{\displaystyle {\int }_{-\pi /2}^{\pi /2}{\cos }^2\theta -2\sin \theta {\cos }^2\theta +\frac{1}{4}\left(1-{\cos }^{2}2\theta \right)d\theta }\\ =\frac{1}{4}ab{h}^2{\left(\left(\frac{\theta }{2}+\frac{\sin 2\theta }{4}\right)+\frac{1}{3}{\cos }^3\theta +\frac{1}{4}\theta -\frac{1}{4}\left(\frac{\theta }{2}+\frac{\sin 4\theta }{8}\right)\right)|}_{-\pi /2}^{\pi /2}\\ =\frac{5}{32}\pi ab{h}^2\end{array}$ (XIV)

Substitute equation (XIII) and (XIV) in equation (XI) to find $\overline{y}$.

$\begin{array}{c}\overline{y}=\frac{\frac{5}{32}\pi ab{h}^2}{\frac{1}{2}\pi abh}\\ =\frac{5}{16}h\end{array}$

Write an expression to calculate ${\displaystyle \int {\overline{z}}_{EL}dV}$.

$\begin{array}{c}{\displaystyle \int {\overline{z}}_{EL}dV}={\displaystyle {\int }_{-b}^{b}z\left(2\frac{a}{b}\sqrt{a^2-z^2}\left(\frac{h}{2b}\right)\left(b-z\right)\right)dz}\\ =\frac{ah}{b^2}{\displaystyle {\int }_{-b}^{b}z\left(b-z\right)\sqrt{b^2-z^2}dz}\\ =\frac{ah}{b^2}{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left(b\sin \theta \right)\left(b\left(1-\sin \theta \right)\right)\left(b\cos \theta \right)\left(b\cos \theta d\theta \right)}\\ =a{b}^{2}h{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left(\sin \theta {\cos }^2\theta -{\sin }^2\theta {\cos }^2\theta \right)d\theta }\\ =a{b}^{2}h{\displaystyle {\int }_{-\pi /2}^{\pi /2}\left(\sin \theta {\cos }^2\theta -\frac{1}{4}\left(1-{\cos }^{2}2\theta \right)\right)d\theta }\\ =a{b}^{2}h{\left(-\frac{1}{3}{\cos }^3\theta -\frac{1}{4}\theta +\frac{1}{4}\left(\frac{\theta }{2}-\frac{\sin 4\theta }{8}\right)\right)|}_{-\pi /2}^{\pi /2}\\ =\frac{1}{8}\pi ab{h}^2\end{array}$ (XV)

Substitute equation (XIII) and (XV) in equation (XII) to find $\overline{z}$.

$\begin{array}{c}\overline{z}=\frac{\frac{1}{8}\pi ab{h}^2}{\frac{1}{2}\pi abh}\\ =-\frac{1}{4}h\end{array}$

Thus, the centroid of the section $\left(\overline{x},\overline{y},\overline{z}\right)$ is $\left(0,\frac{5}{16}h,-\frac{1}{4}h\right)$.