
Vector Mechanics for Engineers: Statics
12th Edition
ISBN: 9781260501735
Author: BEER
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5.4, Problem 5.121P
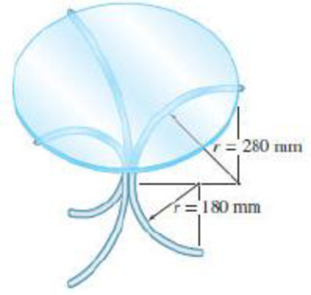
PROBLEM 5.121
The three legs of a small glass-topped table are equally spaced and are made of steel tubing, which has an outside diameter of 24 mm and a cross-sectional area of 150 mm2. The diameter and the thickness of the table top are 600 mm and 10 mm, respectively. Knowing that the density of steel is 7860 kg/m3 and of glass is 2190 kg/m3, locate the center of gravity of the table.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please help
Problem 4. Two circular cylinders partially filled with water and connected at their bases by a tube as
shown below are at rest. Cylinder 1 has radius of 10cm, cylinder 2 has radius of 30cm. Water volume is
1,000 cm³ and the tube contains water, yet the volume of the water in the tube is negligible. Gravity
acts in the -y direction.
a.
Sketch the surfaces of the water in the outlined cylinder pair below that is labeled (a) and
explain on subsequent pages the location and shape of the surface of the water in the two
cylinders.
(a)
d. +1 ms² in y.
e. -1 ms¹² in y.
10cm
y
30cm
X
Next, sketch the surfaces of the water in outlined cylinder pairs (b) to (e) below, and explain on
subsequent pages the location and shape of the eventual steady-state surface of the water in the two
cylinders when they are accelerating:
b. +1 ms² in x.
c. -1 ms¹² in x.
A wastebasket, designed to fit in the corner of a room, has a height of h = 24
in. and has a base in the shape of a quarter circle of radius 10 in. Locate the
center of gravity of the wastebasket, knowing that it is made of sheet metal
of uniform thickness.
10 in.
10 in.
h
The coordinates for the center of gravity are:
in.
|in.
Y
Z :
in.
....
Chapter 5 Solutions
Vector Mechanics for Engineers: Statics
Ch. 5.1 - 5.1 through 5.9 Locate the centroid of the plane...Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.
Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - Locate the centroid of the plane area shown.Ch. 5.1 - PROBLEM 5.16 Determine the y coordinate of the...Ch. 5.1 - Show that as r1 approaches r2, the location of the...Ch. 5.1 - For the area shown, determine the ratio a/b for...Ch. 5.1 - For the semiannular area of Prob. 5.12, determine...Ch. 5.1 - A built-up beam is constructed by nailing seven...Ch. 5.1 - The horizontal x axis is drawn through the...Ch. 5.1 - The horizontal x-axis is drawn through the...Ch. 5.1 - PROBLEM 5.23 The first moment of the shaded area...Ch. 5.1 - A thin, homogeneous wire is bent to form the...Ch. 5.1 - A thin, homogeneous wire is bent to form the...Ch. 5.1 - A thin, homogeneous wire is bent to form the...Ch. 5.1 - A thin, homogeneous wire is bent to form the...Ch. 5.1 - The homogeneous wire ABC is bent into a...Ch. 5.1 - The frame for a sign is fabricated from thin, flat...Ch. 5.1 - The homogeneous wire ABCD is bent as shown and is...Ch. 5.1 - The homogeneous wire ABCD is bent as shown and is...Ch. 5.1 - Determine the distance h for which the centroid of...Ch. 5.1 - Knowing that the distance h has been selected to...Ch. 5.2 - Determine by direct integration the centroid of...Ch. 5.2 - 5.34 through 5.36 Determine by direct integration...Ch. 5.2 - 5.34 through 5.36 Determine by direct integration...Ch. 5.2 - 5.37 through 5.39 Determine by direct integration...Ch. 5.2 - 5.37 through 5.39 Determine by direct integration...Ch. 5.2 - 5.37 through 5.39 Determine by direct integration...Ch. 5.2 - 5.40 and 5.41 Determine by direct integration the...Ch. 5.2 - 5.40 and 5.41 Determine by direct integration the...Ch. 5.2 - Determine by direct integration the centroid of...Ch. 5.2 - 5.43 and 5.44 Determine by direct integration the...Ch. 5.2 - 5.43 and 5.44 Determine by direct integration the...Ch. 5.2 - 5.45 and 5.46 A homogeneous wire is bent into the...Ch. 5.2 - 5.45 and 5.46 A homogeneous wire is bent into the...Ch. 5.2 - A homogeneous wire is bent into the shape shown....Ch. 5.2 - 5.48 and 5.49 Determine by direct integration the...Ch. 5.2 - 5.48 and 5.49 Determine by direct integration the...Ch. 5.2 - Determine the centroid of the area shown in terms...Ch. 5.2 - Determine the centroid of the area shown when a =...Ch. 5.2 - Determine the volume and the surface area of the...Ch. 5.2 - Determine the volume and the surface area of the...Ch. 5.2 - Determine the volume and the surface area of the...Ch. 5.2 - Determine the volume and the surface area of the...Ch. 5.2 - Determine the volume of the solid generated by...Ch. 5.2 - Verify that the expressions for the volumes of the...Ch. 5.2 - Knowing that two equal caps have been removed from...Ch. 5.2 - Three different drive belt profiles are to be...Ch. 5.2 - Determine the capacity, in liters, of the punch...Ch. 5.2 - Determine the volume and total surface area of the...Ch. 5.2 - Determine the volume and weight of the solid brass...Ch. 5.2 - Determine the total surface area of the solid...Ch. 5.2 - Determine the volume of the brass collar obtained...Ch. 5.2 - The shade for a wall-mounted light is formed from...Ch. 5.3 - 5.66 and 5.67 For the beam and loading shown,...Ch. 5.3 - 5.66 and 5.67 For the beam and loading shown,...Ch. 5.3 - 5.68 through 5.73 Determine the reactions at the...Ch. 5.3 - 5.68 through Determine the reactions at the beam...Ch. 5.3 - 5.68 through 5.73 Determine the reactions at the...Ch. 5.3 - 5.68 through Determine the reactions at the beam...Ch. 5.3 - 5.68 through 5.73 Determine the reactions at the...Ch. 5.3 - 5.68 through 5.73 Determine the reactions at the...Ch. 5.3 - Determine (a) the distance a so that the vertical...Ch. 5.3 - Determine (a) the distance a so that the reaction...Ch. 5.3 - Determine the reactions at the beam supports for...Ch. 5.3 - Determine (a) the distributed load w0 at the end D...Ch. 5.3 - The beam AB supports two concentrated loads and...Ch. 5.3 - For the beam and loading of Prob. 5.78, determine...Ch. 5.3 - The cross section of a concrete dam is as shown....Ch. 5.3 - The cross section of a concrete dam is as shown....Ch. 5.3 - The dam for a lake is designed to withstand the...Ch. 5.3 - The base of a dam for a lake is designed to resist...Ch. 5.3 - Prob. 5.84PCh. 5.3 - Prob. 5.85PCh. 5.3 - The 3 4-m side AB of a tank is hinged at its...Ch. 5.3 - The 3 4-m side of an open tank is hinged at its...Ch. 5.3 - A 0.5 0.8-m gate AB is located at the bottom of a...Ch. 5.3 - A 0.5 0.8-m gate AB is located at the bottom of a...Ch. 5.3 - A 4 2-ft gate is hinged at A and is held in...Ch. 5.3 - Fig. P5.90 5.91 Solve Prob. 5.90 if the gate...Ch. 5.3 - A prismatically shaped gate placed at the end of a...Ch. 5.3 - A prismatically shaped gate placed at the end of a...Ch. 5.3 - A long trough is supported by a continuous hinge...Ch. 5.3 - The square gate AB is held in the position shown...Ch. 5.4 - Consider the composite body shown. Determine (a)...Ch. 5.4 - A cone and a cylinder of the same radius a and...Ch. 5.4 - Determine the location of the center of gravity of...Ch. 5.4 - Prob. 5.99PCh. 5.4 - For the stop bracket shown, locate the x...Ch. 5.4 - Fig. P5.100 and P5.101 5.101 For the stop bracket...Ch. 5.4 - Prob. 5.102PCh. 5.4 - Prob. 5.103PCh. 5.4 - For the machine element shown, locate the y...Ch. 5.4 - For the machine element shown, locate the x...Ch. 5.4 - 5.106 and 5.107 Locate the center of gravity of...Ch. 5.4 - 5.106 and 5.107 Locate the center of gravity of...Ch. 5.4 - A corner reflector for tracking by radar has two...Ch. 5.4 - A wastebasket, designed to fit in the corner of a...Ch. 5.4 - An elbow for the duct of a ventilating system is...Ch. 5.4 - A window awning is fabricated from sheet metal...Ch. 5.4 - Locate the center of gravity of the sheet-metal...Ch. 5.4 - Locate the center of gravity of the sheet-metal...Ch. 5.4 - A thin steel wire with a uniform cross section is...Ch. 5.4 - The frame of a greenhouse is constructed from...Ch. 5.4 - Locate the center of gravity of the figure shown,...Ch. 5.4 - Prob. 5.117PCh. 5.4 - A scratch awl has a plastic handle and a steel...Ch. 5.4 - PROBLEM 5.117 A bronze bushing is mounted inside a...Ch. 5.4 - PROBLEM 5.120 A brass collar, of length 2.5 in.,...Ch. 5.4 - PROBLEM 5.121 The three legs of a small...Ch. 5.4 - Prob. 5.122PCh. 5.4 - Determine by direct integration the values of x...Ch. 5.4 - Prob. 5.124PCh. 5.4 - PROBLEM 5.125 Locate the centroid of the volume...Ch. 5.4 - Prob. 5.126PCh. 5.4 - Prob. 5.127PCh. 5.4 - PROBLEM 5.128 Locate the centroid of the volume...Ch. 5.4 - PROBLEM 5.129 Locate the centroid of the volume...Ch. 5.4 - Show that for a regular pyramid of height h and n...Ch. 5.4 - PROBLEM 5.131 Determine by direct integration the...Ch. 5.4 - PROBLEM 5.132 The sides and the base of a punch...Ch. 5.4 - Locate the centroid of the section shown, which...Ch. 5.4 - Locate the centroid of the section shown, which...Ch. 5.4 - Determine by direct integration the location of...Ch. 5.4 - Alter grading a lot, a builder places four stakes...Ch. 5 - 5.137 and 5.138 Locate the centroid of the plane...Ch. 5 - 5.137 and 5.138 Locate the centroid of the plane...Ch. 5 - Prob. 5.139RPCh. 5 - Determine by direct integration the centroid of...Ch. 5 - Determine by direct integration the centroid of...Ch. 5 - The escutcheon (a decorative plate placed on a...Ch. 5 - Determine the reactions at the supports for the...Ch. 5 - A beam is subjected to a linearly distributed...Ch. 5 - A tank is divided into two sections by a 1 1-m...Ch. 5 - Determine the y coordinate of the centroid of the...Ch. 5 - An 8-in.-diameter cylindrical duct and a 4 8-in....Ch. 5 - Three brass plates are brazed to a steel pipe to...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- For the semiannular area of Prob. 5.12, determine the ratio r1 to r2 so that the centroid of the area is located at x = -1/2 r2 and y= 0.(Reference to Problem 5.12):Locate the centroid of the plane area shown.arrow_forwardThe aluminum shade for the small high-intensity lamp shown has a uniform thickness of 1 mm. Knowing that the density of aluminium is 2800 kg/m3, , determine the mass of the shade.arrow_forwardFor the tank of water shown below, the radius of the circular surface is R=1.0 m, h=1.0m, and the length of the tank is w=2.0 m. Determine (1) the correct expression of the area magnitude whose volume weight is equivalent to the vertical force exerted on the whole curved surfaces_________ A. B. C. D.arrow_forward
- Problem 3.7 The simple structure shown in Fig 3.35 is called a cantilever beam and is one of the fundamental mechanical elements in engineering. A cantilever beam is fixed at one end and free at the other. In Fig. 3.35, the fixed and free ends of the beam are identified as points A and C, respectively. Point B correspondks to the center of gravity of in the beam. Assume that the beam shown has a weight W = 100 N and a length /=1m. A force with magnitude F= 150 N is applied at the free-end of the beam in a direction that makes an angle 0- 45" with the hon zontal. Determine the magnitude and direction of the net moment developed at the fixed-end of the be am, Pr Fig arm the f (a) I th WE ex ind Answer, MA 56 N-m (ccw). Fig. 3.35 A cantuleverlam Fig. 3.37 IPro ype here to searcharrow_forwardProblem 4.1Given: A barge may be assumed as a rectangular prism (or cuboid) with a length between perpendiculars of 70 ft., a beam of 30 ft., and a depth of ship of 6 ft. The ship weighs 150 tons (US “short ton”) and this weight may be assumed uniformly distributed in the volume of the ship. The following Cargo was loaded along the center line of the ship relative to the deck (top) of the ship. Required: Considering ONLY transverse stability,a) Find the buoyant force and draft of the vessel.arrow_forwardA bronze bushing is mounted inside a steel sleeve. Knowing that the specific weight of bronze is 0.318 lb/in³ and of steel is 0.284 lb/in³, determine the location of the center of gravity of the assembly. It is given that d = 0.38 in. -1.125 in. TY 0.75 in -1.80 in.- The center of gravity of the assembly is: in. in. in. KTN X Y Z ZE 1.00 in. 0.40 in. Xarrow_forward
- Show that for a regular pyramid of height h and n sides (n = 3, 4, . . .) the centroid of the volume of the pyramid is located at a distance h /4 above the base.arrow_forwardA bronze bushing is mounted inside a steel sleeve. Knowing that the specific weight of bronze is 0.318 lb/in3 and of steel is 0.284 lb/in3 , determine the location of the center of gravity of the assembly.arrow_forwardThree brass plates are brazed to a steel pipe to form the flagpole base shown. Knowing that the pipe has a wall thickness of 8 mm and that each plate is 6 mm thick, determine the location of the center of gravity of the base. (Densities: brass =8470 kg/m3, steel=7860 kg/m3.)arrow_forward
- The X coordinate of the centroid of a right- angled triangle of base b and height h isarrow_forwardProblem No. 1: steel •Determine the gravitational force in N which the copper sphere exerts on the steel homogeneous, and the value of r is 50 mm. Density of copper and steel are 8910 2r sphere. Both spheres are 4r kg/m3 respectively. and 7830 kg/m3, copperarrow_forwardThe coordinates of the centroid of the line are = 332 and = 102. Use the first Pappus Guldinus theorem to determine the area, in m2, of the surface of revolution obtained by revolving the line about the x-axis. The coordinates of the centroid of the area between the x-axis and the line in Question 9 are = 357 and = 74.1. Use the second Pappus Guldinus theorem to determine the volume obtained, in m3, by revolving the area about the x-axis.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Mechanical Engineering: Centroids & Center of Gravity (1 of 35) What is Center of Gravity?; Author: Michel van Biezen;https://www.youtube.com/watch?v=Tkyk-G1rDQg;License: Standard Youtube License