Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
8th Edition
ISBN: 9781259676512
Author: Kenneth H Rosen
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.4, Problem 28E
many additions are used by the recursive and iterative algorithms given in Algorithms 7 and 8, respectively, to find the Fibonacci number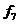
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below.
Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship.
Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship.
Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size).
Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear regression model.
Interpret the…
Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. How to take snapshots: if you use a MacBook, press Command+ Shift+4 to take snapshots. If you are using Windows, use the Snipping Tool to take snapshots.
Question 1: Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship.
Value of correlation coefficient:
Direction of the relationship (positive, negative, or zero relationship):
Strength of the relationship (strong/moderate/weak):
Question 2: Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size. (The answer for the…
Tri-County Utilities, Inc., supplies natural gas to customers in a three-county area. The company purchases natural gas from two companies: Southern Gas and Northwest Gas.
Demand forecasts for the coming winter season are as follows: Hamilton County, 400 units; Butler County, 200 units; and Clermont County, 300 units. Contracts to provide the following quantities have been written: Southern Gas, 500 units; and Northwest Gas, 400 units. Distribution costs for the counties vary, depending upon the location of the suppliers. The distribution costs per unit (in thousands of dollars)
are as follows.
From
To
Hamilton Butler
Clermont
Southern Gas
10
20
15
Northwest Gas
12
15
18
(a) Develop a network representation of this problem. (Submit a file with a maximum size of 1 MB.)
Choose File No file chosen
Assignment 3 graph.docx
Score: 1 out of 1
Comment:
(b) Develop a linear programming model that can be used to determine the plan that will minimize total distribution costs (in thousands of…
Chapter 5 Solutions
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
Ch. 5.1 - re are infinite]y many stations on a train route....Ch. 5.1 - pose that you know that a golfer plays theho1e of...Ch. 5.1 - P(n) be the statement...Ch. 5.1 - P(n) be the statementthat 13+ 23+ ... + n3=...Ch. 5.1 - ve...Ch. 5.1 - ve that1.1!+2.2!+...n.n!=(n+1)!1whenevernis a...Ch. 5.1 - ve that3+3.5+3.52+...+3.5n=3(5n+11)/4whenevernis a...Ch. 5.1 - ve that22.7+2.72...+2(7)n=(1(7)n+1)/4whenevernis a...Ch. 5.1 - a)Find a formula for the sum of the firstneven...Ch. 5.1 - a) Find a formula for 112+123++1m(n+1) by...
Ch. 5.1 - a) Find a formula for 12+14+18+...+12n by...Ch. 5.1 - ve that j=0n(12)=2n+1+(1)n32n whenevernis a...Ch. 5.1 - ve that1222+32...+(1)n1n2=(1)n1n(n+1)/2whenevernis...Ch. 5.1 - ve that for every positive...Ch. 5.1 - ve that for every positive integern,...Ch. 5.1 - ve that for every positive integern,...Ch. 5.1 - ve thatj=1nj4=n(n+1)(2n+1)(3n2+3n1)/30whenevernis...Ch. 5.1 - P(n) be the statement thatn!< nn, where n is an...Ch. 5.1 - P(n)be tie statement that 1+14+19+...+1n221n,...Ch. 5.1 - ve that3nn!if n is an integer greater than6.Ch. 5.1 - ve that2nn2ifnis an integer greater than 4.Ch. 5.1 - Prob. 22ECh. 5.1 - which nonnegative integersnis2n+32n?Prove your...Ch. 5.1 - ve that1/(2n)[1.3.5..(2n1)]/(2.4....2n)whenevernis...Ch. 5.1 - ve that ifhi,then1+nh(1+h)nfor all nonnegative...Ch. 5.1 - pose that a and b are real numbers with o< b< a....Ch. 5.1 - ve that for every positive integern,...Ch. 5.1 - ve thatn27n+12is nonnegative whenevernis an...Ch. 5.1 - Prob. 29ECh. 5.1 - ve that H1+H2+...+Hn=(n+1)HnnCh. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - mathematical induction in Exercises 31-37 to prove...Ch. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - Prob. 43ECh. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - mathematical induction in Exercises 38-46 to prove...Ch. 5.1 - Exercises 47 and 48 we consider the problem of...Ch. 5.1 - In Exercises 47 and 48 we consider the problem of...Ch. 5.1 - rcises 49-51 present incorrect proofs using...Ch. 5.1 - Exercises 49-51 present incorrect proofs using...Ch. 5.1 - rcises 49-51 present incorrect proofs using...Ch. 5.1 - pose thatmandnare positive integers withm >nandfis...Ch. 5.1 - Prob. 53ECh. 5.1 - mathematical induction to show that given a set...Ch. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - 57.(Requires calculus) use mathematical induction...Ch. 5.1 - pose that A and B are square matrices with the...Ch. 5.1 - Prob. 59ECh. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - w that n lines separate the plane into (n2+n+ 2)/...Ch. 5.1 - A=(a1+a2+...+an)/nG= and the geometric mean of...Ch. 5.1 - Prob. 64ECh. 5.1 - Prob. 65ECh. 5.1 - Prob. 66ECh. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - pose there arenpeople in a group, each aware of a...Ch. 5.1 - pose there arenpeople in a group, each aware of a...Ch. 5.1 - Prob. 71ECh. 5.1 - pose there arenpeople in a group, each aware of a...Ch. 5.1 - Prob. 73ECh. 5.1 - etimes ire cannot use mathematical induction to...Ch. 5.1 - Prob. 75ECh. 5.1 - etimes we cannot use mathematical induction to...Ch. 5.1 - nbe an even integer. Show that it is people to...Ch. 5.1 - Prob. 78ECh. 5.1 - .Construct a ling using right triominoes of the 8...Ch. 5.1 - ve or disprovethatall checkerboards of these...Ch. 5.1 - w that a three-dimensional2n2n2ncheckerboard with...Ch. 5.1 - w that annncheckerboard with on square removed can...Ch. 5.1 - w that acheckerboard with a corner square removed...Ch. 5.1 - Prob. 84ECh. 5.1 - Prob. 85ECh. 5.2 - Use strong induction to show that if you can run...Ch. 5.2 - strong induction to show that all dominoes fall in...Ch. 5.2 - P(n)be the statement that a postage ofncents can...Ch. 5.2 - P(n)be the statement that a postage of n cents can...Ch. 5.2 - a)Determine which amounts of postage can be formed...Ch. 5.2 - a)Determine which amounts of postage can be formed...Ch. 5.2 - ch amount of money can b formed using just two...Ch. 5.2 - pose that a store offers gift certificates in...Ch. 5.2 - song induction to prove that2is irrational. [Hint:...Ch. 5.2 - Assume that a chocolate bar consists ofnsquares...Ch. 5.2 - sider this variation of the game of Nim. The game...Ch. 5.2 - . Use strong induction to show that every positive...Ch. 5.2 - A jigsaw puzzle is put together by successively...Ch. 5.2 - Supposeyou begin with apile ofnstones and split...Ch. 5.2 - Prob. 15ECh. 5.2 - ve that the first player has a winning strategy...Ch. 5.2 - strong induction to show that if a simple polygon...Ch. 5.2 - strong induction to show that a simple po1gonPwith...Ch. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - the proof ofLemma 1we mentioned that many...Ch. 5.2 - rcises 22 and 23 present examples that show...Ch. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - pose thatP(n) is a propositional function....Ch. 5.2 - pose that ifp(n) is a propositional function....Ch. 5.2 - w that if the statement is for infinitely many...Ch. 5.2 - bbe a fix integer and a fixed positive integer....Ch. 5.2 - Prob. 29ECh. 5.2 - d the flaw with the following "proof" thatan=1 for...Ch. 5.2 - w that strong induction is a valid method of proof...Ch. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - ve that (math) for all positive integerskandn,...Ch. 5.2 - Prob. 35ECh. 5.2 - well-orderingproperty can be used to show that...Ch. 5.2 - a be an integer and b be a positive integer. Show...Ch. 5.2 - Prob. 38ECh. 5.2 - you u se th e well - ord ering pr operty to pr o v...Ch. 5.2 - Prob. 40ECh. 5.2 - w that the well-ordering property can be proved...Ch. 5.2 - w that principle of mathematical induction and...Ch. 5.2 - Prob. 43ECh. 5.3 - Findf(1),f(2),f(3), andf(4) iff(n) is defined...Ch. 5.3 - Findf(1),f(2),f(3),f(4), andf(5)iff(n)is defined...Ch. 5.3 - LetP(n) bethestatementthata postage ofncents can...Ch. 5.3 - Prob. 4ECh. 5.3 - Determine which amounts of postage can be formed...Ch. 5.3 - Determine which amounts of postage can be formed...Ch. 5.3 - e a recursive definition of the...Ch. 5.3 - Give a recursive definition of the sequence...Ch. 5.3 - Fbe the function such thatF(n) is the sum of the...Ch. 5.3 - en a recursive definition ofsm(n), the sum of the...Ch. 5.3 - e a recursive definition ofPm(n), the product of...Ch. 5.3 - Exercises 12—19fnis the nth Fibonacci 12.Prove...Ch. 5.3 - Exercises1219fnis the nth Fibonacci number....Ch. 5.3 - Exercises 12—l9fnis the nth Fibonacci *14.Show...Ch. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Exercises 12-19fnis thenthFibonacci number....Ch. 5.3 - Exercises 12-19fnis thenthFibonacci number. 18....Ch. 5.3 - Prob. 19ECh. 5.3 - e a recursive definition of the if functions max...Ch. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - e a recursive definition of a)the set of odd...Ch. 5.3 - e a recursive definition of a)the set of even...Ch. 5.3 - Sbe the set of positive integers defined by Basis...Ch. 5.3 - Sbe the set of positive integers defined by Basis...Ch. 5.3 - Sbe the subset of the set of ordered pairs of...Ch. 5.3 - Sbe the subset of the set of ordered pairs of...Ch. 5.3 - e a recursive definition of each ofthesesets of...Ch. 5.3 - e arecursive definition of each of these sets of...Ch. 5.3 - ve that in a bit string, the string 01 occurs at...Ch. 5.3 - ine well-formed formulae of sets, variables...Ch. 5.3 - Prob. 34ECh. 5.3 - Give a recursive definition of the...Ch. 5.3 - d the reversal of the following bit strings....Ch. 5.3 - e a recursive definition of the reversal of a...Ch. 5.3 - structural induction to prove that(w1w2)R=w2Rw1R.Ch. 5.3 - Prob. 39ECh. 5.3 - the well-ordermg property to show that ifxandyare...Ch. 5.3 - n does a swing belong to eset Aof bit stings...Ch. 5.3 - ursively define the set of bit strings that have...Ch. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - structural induction to show thatn(T)>&[I)+inhere...Ch. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - generalized induction as was doneinExample 13to...Ch. 5.3 - A partition of a positive integer nis amy to...Ch. 5.3 - Prob. 50ECh. 5.3 - sider the Mowing inductive definition of a version...Ch. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - sider the Mowing inductive definition of a version...Ch. 5.3 - sider the Mowing inductive definition of a version...Ch. 5.3 - Prob. 56ECh. 5.3 - sider the Mowing inductive definition of a version...Ch. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - rcises 62-64 deal with iterations of the logarithm...Ch. 5.3 - rcises 62-64 deal with iterations of the logarithm...Ch. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - f(n)=n/2.Find a formula forf(k)(n).What is the...Ch. 5.3 - Prob. 67ECh. 5.4 - ce Algorithm 1when it is givenn= 5 as input, That...Ch. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - ce Algorithm 4 when it is given In=5,n= 11, andb=3...Ch. 5.4 - ce Algorithm 4 when it ism=7,n=10, andb=2 as...Ch. 5.4 - Prob. 7ECh. 5.4 - e a recursive algorithm for finding the sum of the...Ch. 5.4 - Prob. 9ECh. 5.4 - e a recursive algorithm for finding the maximum of...Ch. 5.4 - Prob. 11ECh. 5.4 - ise a recursive algorithm for...Ch. 5.4 - e a recursive algorithm for...Ch. 5.4 - Give a recursive algorithm for finding mode of a...Ch. 5.4 - ise a recursive algorithm for computing the...Ch. 5.4 - ve that the recursive algorithm for finding the...Ch. 5.4 - Prob. 17ECh. 5.4 - ve that Algorithm 1 for computingn! whennis a...Ch. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - ve that the recursive algorithm that you found in...Ch. 5.4 - ise a recursive algorithm for computing for...Ch. 5.4 - ise a recursive algorithm to finda2n, whereais a...Ch. 5.4 - Prob. 25ECh. 5.4 - the algorithm in Exercise 24 to devise an...Ch. 5.4 - does the number of multiplication used by the...Ch. 5.4 - many additions are used by the recursive and...Ch. 5.4 - ise a recursive algorithm to find thenthterm of...Ch. 5.4 - ise an iterative algorithm to find the nth term of...Ch. 5.4 - Prob. 31ECh. 5.4 - ise a recursive algorithm to find the nth term of...Ch. 5.4 - Prob. 33ECh. 5.4 - the recursive or the iterative algorithm for...Ch. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - e algorithm for finding the reversal of a bit...Ch. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - ve that the recursive algorithm for finding the...Ch. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - a merge sort to sort 4.3,2,5, i, 8, 7, 6 into...Ch. 5.4 - Prob. 45ECh. 5.4 - many comparisons are required to merge these pairs...Ch. 5.4 - Prob. 47ECh. 5.4 - What theleast number comparisons needed to merge...Ch. 5.4 - ve that the merge sort algorithm is correct.Ch. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - quick sort is an efficient algorithm. To...Ch. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.5 - ve that the program segment y:=1z:=x+y is correct...Ch. 5.5 - ify that the program segment ifx0thenx:=0 is...Ch. 5.5 - ify that the progr am segment is correct with...Ch. 5.5 - Prob. 4ECh. 5.5 - ise a rule of inference for verification of...Ch. 5.5 - the rule of inference developed in Exercise 5 to...Ch. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - a loop invariant to verify thattheEuclidean...Ch. 5 - Can you use theprinciple of mathematical induction...Ch. 5 - a) For which positive integersnis iin+ 17 S b)...Ch. 5 - Which amounts of postage can be formed using only...Ch. 5 - e two different examples of proofs that use strong...Ch. 5 - a) State the well-ordering property for the set of...Ch. 5 - Prob. 6RQCh. 5 - Prob. 7RQCh. 5 - Prob. 8RQCh. 5 - Prob. 9RQCh. 5 - Prob. 10RQCh. 5 - Prob. 11RQCh. 5 - Prob. 12RQCh. 5 - Prob. 13RQCh. 5 - Prob. 14RQCh. 5 - Prob. 15RQCh. 5 - Prob. 16RQCh. 5 - Prob. 1SECh. 5 - Prob. 2SECh. 5 - mathematica1 induction to show...Ch. 5 - Prob. 4SECh. 5 - Prob. 5SECh. 5 - mathematical induction to show...Ch. 5 - Prob. 7SECh. 5 - d an integ N such that2nn4whenevernan integer...Ch. 5 - Prob. 9SECh. 5 - Prob. 10SECh. 5 - Prob. 11SECh. 5 - Prob. 12SECh. 5 - Prob. 13SECh. 5 - Prob. 14SECh. 5 - Prob. 15SECh. 5 - Prob. 16SECh. 5 - Prob. 17SECh. 5 - Prob. 18SECh. 5 - mulate a conjecture about which Fibonacci nubs are...Ch. 5 - Prob. 20SECh. 5 - Prob. 21SECh. 5 - w thatfn+fn+2=ln+1whenevernis a positive integer,...Ch. 5 - Prob. 23SECh. 5 - Prob. 24SECh. 5 - Prob. 25SECh. 5 - Prob. 26SECh. 5 - Prob. 27SECh. 5 - (Requires calculus)Suppose that the...Ch. 5 - w ifnis a positive integer withn>2, then...Ch. 5 - Prob. 30SECh. 5 - Prob. 31SECh. 5 - (Requires calculus) Use mathematical induction and...Ch. 5 - Prob. 33SECh. 5 - Prob. 34SECh. 5 - Prob. 35SECh. 5 - mathematical induction to prove that ifx1,x2,...Ch. 5 - mathematical induction to prove that ifnpeople...Ch. 5 - pose that for every pair of cities in a country...Ch. 5 - Prob. 39SECh. 5 - Prob. 40SECh. 5 - Prob. 41SECh. 5 - Prob. 42SECh. 5 - Use mathematical induction to show that ifnis a...Ch. 5 - Prob. 44SECh. 5 - Prob. 45SECh. 5 - Prob. 46SECh. 5 - Prob. 47SECh. 5 - Prob. 48SECh. 5 - Prob. 49SECh. 5 - w thatnplanes divide three-dimensional...Ch. 5 - Prob. 51SECh. 5 - Prob. 52SECh. 5 - Prob. 53SECh. 5 - Prob. 54SECh. 5 - Prob. 55SECh. 5 - Prob. 56SECh. 5 - Prob. 57SECh. 5 - Prob. 58SECh. 5 - Prob. 59SECh. 5 - d all balanced string of parentheses with exactly...Ch. 5 - Prob. 61SECh. 5 - Prob. 62SECh. 5 - Prob. 63SECh. 5 - Prob. 64SECh. 5 - e a recursive algorithm for finding all balanced...Ch. 5 - Prob. 66SECh. 5 - Prob. 67SECh. 5 - Prob. 68SECh. 5 - Prob. 69SECh. 5 - Prob. 70SECh. 5 - Prob. 71SECh. 5 - Prob. 72SECh. 5 - Prob. 73SECh. 5 - Prob. 74SECh. 5 - Prob. 75SECh. 5 - Prob. 76SECh. 5 - Prob. 77SECh. 5 - Prob. 1CPCh. 5 - Prob. 2CPCh. 5 - Prob. 3CPCh. 5 - Prob. 4CPCh. 5 - Prob. 5CPCh. 5 - Prob. 6CPCh. 5 - Prob. 7CPCh. 5 - Prob. 8CPCh. 5 - Prob. 9CPCh. 5 - Prob. 10CPCh. 5 - en a nonnegative integern,find the nth Fibonacci...Ch. 5 - Prob. 12CPCh. 5 - Prob. 13CPCh. 5 - Prob. 14CPCh. 5 - en a list of integers, sort these integers using...Ch. 5 - Prob. 1CAECh. 5 - Prob. 2CAECh. 5 - Prob. 3CAECh. 5 - Prob. 4CAECh. 5 - Prob. 5CAECh. 5 - Prob. 6CAECh. 5 - Prob. 7CAECh. 5 - pare either number of operations or the needed to...Ch. 5 - cribe the origins of mathematical induction. Who...Ch. 5 - lain how to prove the Jordan curve theorem for...Ch. 5 - Prob. 3WPCh. 5 - cribe a variety of different app1icaons of the...Ch. 5 - Prob. 5WPCh. 5 - e die recursive definition of Knuth’s up-arrow...Ch. 5 - Prob. 7WPCh. 5 - lain how the ideas and concepts of program...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Use the method of undetermined coefficients to solve the given nonhomogeneous system. dx dt = 2x + 3y − 8 dy dt = −x − 2y + 6 X(t) =arrow_forwardAs discussed in Section 8.3, the Markowitz model uses the variance of the portfolio as the measure of risk. However, variance includes deviations both below and above the mean return. Semivariance includes only deviations below the mean and is considered by many to be a better measure of risk. (a) Develop a model that minimizes semivariance for the Hauck Financial data given in the file HauckData with a required return of 10%. Assume that the five planning scenarios in the Hauck Financial Services model are equally likely to occur. Hint: Modify model (8.10)–(8.19). Define a variable ds for each scenario and let ds ≥ R − Rs with ds ≥ 0. Then make the objective function: Min 1 5 5 s = 1 ds2. Let FS = proportion of portfolio invested in the foreign stock mutual fund IB = proportion of portfolio invested in the intermediate-term bond fund LG = proportion of portfolio invested in the large-cap growth fund LV = proportion of portfolio invested in the large-cap value fund…arrow_forwardCalculus lll May I please have the blank lines completed, and final statement defined as a result? Thank you for the support!arrow_forward
- For each month of the year, Taylor collected the average high temperatures in Jackson, Mississippi. He used the data to create the histogram shown. Which set of data did he use to create the histogram? A 55, 60, 64, 72, 73, 75, 77, 81, 83, 91, 91, 92\ 55,\ 60,\ 64,\ 72,\ 73,\ 75,\ 77,\ 81,\ 83,\ 91,\ 91,\ 92 55, 60, 64, 72, 73, 75, 77, 81, 83, 91, 91, 92 B 55, 57, 60, 65, 70, 71, 78, 79, 85, 86, 88, 91\ 55,\ 57,\ 60,\ 65,\ 70,\ 71,\ 78,\ 79,\ 85,\ 86,\ 88,\ 91 55, 57, 60, 65, 70, 71, 78, 79, 85, 86, 88, 91 C 55, 60, 63, 64, 65, 71, 83, 87, 88, 88, 89, 93\ 55,\ 60,\ 63,\ 64,\ 65,\ 71,\ 83,\ 87,\ 88,\ 88,\ 89,\ 93 55, 60, 63, 64, 65, 71, 83, 87, 88, 88, 89, 93 D 55, 58, 60, 66, 68, 75, 77, 82, 86, 89, 91, 91\ 55,\ 58,\ 60,\ 66,\ 68,\ 75,\ 77,\ 82,\ 86,\ 89,\ 91,\ 91 55, 58, 60, 66, 68, 75, 77, 82, 86, 89, 91, 91arrow_forwardIn this problem, we consider a Brownian motion (W+) t≥0. We consider a stock model (St)t>0 given (under the measure P) by d.St 0.03 St dt + 0.2 St dwt, with So 2. We assume that the interest rate is r = 0.06. The purpose of this problem is to price an option on this stock (which we name cubic put). This option is European-type, with maturity 3 months (i.e. T = 0.25 years), and payoff given by F = (8-5)+ (a) Write the Stochastic Differential Equation satisfied by (St) under the risk-neutral measure Q. (You don't need to prove it, simply give the answer.) (b) Give the price of a regular European put on (St) with maturity 3 months and strike K = 2. (c) Let X = S. Find the Stochastic Differential Equation satisfied by the process (Xt) under the measure Q. (d) Find an explicit expression for X₁ = S3 under measure Q. (e) Using the results above, find the price of the cubic put option mentioned above. (f) Is the price in (e) the same as in question (b)? (Explain why.)arrow_forwardProblem 4. Margrabe formula and the Greeks (20 pts) In the homework, we determined the Margrabe formula for the price of an option allowing you to swap an x-stock for a y-stock at time T. For stocks with initial values xo, yo, common volatility σ and correlation p, the formula was given by Fo=yo (d+)-x0Þ(d_), where In (±² Ꭲ d+ õ√T and σ = σ√√√2(1 - p). дго (a) We want to determine a "Greek" for ỡ on the option: find a formula for θα (b) Is дго θα positive or negative? (c) We consider a situation in which the correlation p between the two stocks increases: what can you say about the price Fo? (d) Assume that yo< xo and p = 1. What is the price of the option?arrow_forward
- The Course Name Real Analysis please Solve questions by Real Analysisarrow_forwardWe consider a 4-dimensional stock price model given (under P) by dẴ₁ = µ· Xt dt + йt · ΣdŴt where (W) is an n-dimensional Brownian motion, π = (0.02, 0.01, -0.02, 0.05), 0.2 0 0 0 0.3 0.4 0 0 Σ= -0.1 -4a За 0 0.2 0.4 -0.1 0.2) and a E R. We assume that ☑0 = (1, 1, 1, 1) and that the interest rate on the market is r = 0.02. (a) Give a condition on a that would make stock #3 be the one with largest volatility. (b) Find the diversification coefficient for this portfolio as a function of a. (c) Determine the maximum diversification coefficient d that you could reach by varying the value of a? 2arrow_forwardQuestion 1. Your manager asks you to explain why the Black-Scholes model may be inappro- priate for pricing options in practice. Give one reason that would substantiate this claim? Question 2. We consider stock #1 and stock #2 in the model of Problem 2. Your manager asks you to pick only one of them to invest in based on the model provided. Which one do you choose and why ? Question 3. Let (St) to be an asset modeled by the Black-Scholes SDE. Let Ft be the price at time t of a European put with maturity T and strike price K. Then, the discounted option price process (ert Ft) t20 is a martingale. True or False? (Explain your answer.) Question 4. You are considering pricing an American put option using a Black-Scholes model for the underlying stock. An explicit formula for the price doesn't exist. In just a few words (no more than 2 sentences), explain how you would proceed to price it. Question 5. We model a short rate with a Ho-Lee model drt = ln(1+t) dt +2dWt. Then the interest rate…arrow_forward
- In this problem, we consider a Brownian motion (W+) t≥0. We consider a stock model (St)t>0 given (under the measure P) by d.St 0.03 St dt + 0.2 St dwt, with So 2. We assume that the interest rate is r = 0.06. The purpose of this problem is to price an option on this stock (which we name cubic put). This option is European-type, with maturity 3 months (i.e. T = 0.25 years), and payoff given by F = (8-5)+ (a) Write the Stochastic Differential Equation satisfied by (St) under the risk-neutral measure Q. (You don't need to prove it, simply give the answer.) (b) Give the price of a regular European put on (St) with maturity 3 months and strike K = 2. (c) Let X = S. Find the Stochastic Differential Equation satisfied by the process (Xt) under the measure Q. (d) Find an explicit expression for X₁ = S3 under measure Q. (e) Using the results above, find the price of the cubic put option mentioned above. (f) Is the price in (e) the same as in question (b)? (Explain why.)arrow_forward3. Consider the polynomial equation 6-iz+7z² - iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forwardThe managing director of a consulting group has the accompanying monthly data on total overhead costs and professional labor hours to bill to clients. Complete parts a through c. Question content area bottom Part 1 a. Develop a simple linear regression model between billable hours and overhead costs. Overhead Costsequals=212495.2212495.2plus+left parenthesis 42.4857 right parenthesis42.485742.4857times×Billable Hours (Round the constant to one decimal place as needed. Round the coefficient to four decimal places as needed. Do not include the $ symbol in your answers.) Part 2 b. Interpret the coefficients of your regression model. Specifically, what does the fixed component of the model mean to the consulting firm? Interpret the fixed term, b 0b0, if appropriate. Choose the correct answer below. A. The value of b 0b0 is the predicted billable hours for an overhead cost of 0 dollars. B. It is not appropriate to interpret b 0b0, because its value…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY