Precalculus with Limits

3rd Edition

ISBN: 9781133947202

Author: Ron Larson

Publisher: Cengage Learning

See similar textbooks

Concept explainers

Minimization

In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…

Maxima and Minima

The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.

Derivatives

A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …

Concavity

In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …

Videos

Question

Chapter 5.3, Problem 79E

(a)

To determine

To find : the maximum and minimum point of the function

(a)

Expert Solution

Answer to Problem 79E

The maximum points of the function are (π/3, 1.25) & (5π/3, 1.25) _ radians.

The minimum point of the function are (0,1)&(π, -1) _ radians.

Explanation of Solution

Given information : Function f(x)=sin2x+cosx ; Trigonometric Equation 2sinxcosx−sinx=0 ; [0,2π)

Concept Involved:

A maximum is a high point and a minimum is a low point over the given interval.

Graph:

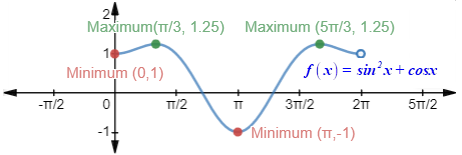
Precalculus with Limits, Chapter 5.3, Problem 79E

Interpretation:

The graph shows, at x=π/3 &5π/3 radians the graph has the maximum value of 1.25 and at x=0 &π radians the graph has the minimum value of 1&−1 respectively.

(b)

To determine

To find : all the solutions of the trigonometric equations in the given interval

(b)

Expert Solution

Answer to Problem 79E

The solution to the given trigonometric equation are x=0, π/3, π, & 5π/3 _ radians.

Explanation of Solution

Given information : Function f(x)=sin2x+cosx ; Trigonometric Equation 2sinxcosx−sinx=0 ; [0,2π)

Concept Involved:

Solution to a quadratic equation are the values of x that makes the equation TRUE.

To solve a trigonometric equation, use standard algebraic techniques (when possible) such as collecting like terms, extracting square roots, and factoring.

Our preliminary goal in solving a trigonometric equation is to isolate the trigonometric function on one side of the equation.

Calculation:

Factor the Greatest Common Factor of left side of the equation 2sinxcosx−sinx=0

sinx(2cosx−1)=0

Using the zero factor property which states that if a⋅b=0 then a=0 (or) b=0 , we need to set each factor to zero.

sinx=0▶1^s^t equation

2cosx−1=0▶2ⁿ^d equation

Solving the 1^s^t equation and finding x values that makes it true in the interval [0,2π)

x=sin−1(0)

x=0, π

Solving the 2ⁿ^d equation and finding x values that makes it true in the interval [0,2π)

By adding 1 on both sides of the equation
By simplifying on both sides of the equation
By dividing 2 on both sides of the equation
By simplifying fraction on both sides of the equation

2cosx−1=02cosx=12cosx2=12cosx=12x=cos−1(12)x=π3, 5π3

Conclusion:

x=0, π3, π, &5π3 radians are the zero of the function and solution to the equation 2sinxcosx−sinx=0 in the interval [0,2π)

Chapter 5.3, Problem 78E

Chapter 5.3, Problem 80E

Chapter 5 Solutions

Precalculus with Limits

Ch. 5.1 - Prob. 1E Ch. 5.1 - Prob. 2E Ch. 5.1 - Prob. 3E Ch. 5.1 - Prob. 4E Ch. 5.1 - Prob. 5E Ch. 5.1 - Prob. 6E Ch. 5.1 - Prob. 7E Ch. 5.1 - Prob. 8E Ch. 5.1 - Prob. 9E Ch. 5.1 - Prob. 10E

Ch. 5.1 - Prob. 11E Ch. 5.1 - Prob. 12E Ch. 5.1 - Prob. 13E Ch. 5.1 - Prob. 14E Ch. 5.1 - Prob. 15E Ch. 5.1 - Prob. 16E Ch. 5.1 - Prob. 17E Ch. 5.1 - Prob. 18E Ch. 5.1 - Prob. 19E Ch. 5.1 - Prob. 20E Ch. 5.1 - Prob. 21E Ch. 5.1 - Prob. 22E Ch. 5.1 - Prob. 23E Ch. 5.1 - Prob. 24E Ch. 5.1 - Prob. 25E Ch. 5.1 - Prob. 26E Ch. 5.1 - Prob. 27E Ch. 5.1 - Prob. 28E Ch. 5.1 - Prob. 29E Ch. 5.1 - Prob. 30E Ch. 5.1 - Prob. 31E Ch. 5.1 - Prob. 32E Ch. 5.1 - Prob. 33E Ch. 5.1 - Prob. 34E Ch. 5.1 - Prob. 35E Ch. 5.1 - Prob. 36E Ch. 5.1 - Prob. 37E Ch. 5.1 - Prob. 38E Ch. 5.1 - Prob. 39E Ch. 5.1 - Prob. 40E Ch. 5.1 - Prob. 41E Ch. 5.1 - Prob. 42E Ch. 5.1 - Prob. 43E Ch. 5.1 - Prob. 44E Ch. 5.1 - Prob. 45E Ch. 5.1 - Prob. 46E Ch. 5.1 - Prob. 47E Ch. 5.1 - Prob. 48E Ch. 5.1 - Prob. 49E Ch. 5.1 - Prob. 50E Ch. 5.1 - Prob. 51E Ch. 5.1 - Prob. 52E Ch. 5.1 - Prob. 53E Ch. 5.1 - Prob. 54E Ch. 5.1 - Prob. 55E Ch. 5.1 - Prob. 56E Ch. 5.1 - Prob. 57E Ch. 5.1 - Prob. 58E Ch. 5.1 - Prob. 59E Ch. 5.1 - Prob. 60E Ch. 5.1 - Prob. 61E Ch. 5.1 - Prob. 62E Ch. 5.1 - Prob. 63E Ch. 5.1 - Prob. 64E Ch. 5.1 - Prob. 65E Ch. 5.1 - Prob. 66E Ch. 5.1 - Prob. 67E Ch. 5.1 - Prob. 68E Ch. 5.1 - Prob. 69E Ch. 5.1 - Prob. 70E Ch. 5.1 - Prob. 71E Ch. 5.1 - Prob. 72E Ch. 5.1 - Prob. 73E Ch. 5.1 - Prob. 74E Ch. 5.1 - Prob. 75E Ch. 5.1 - Prob. 76E Ch. 5.2 - Prob. 1E Ch. 5.2 - Prob. 2E Ch. 5.2 - Prob. 3E Ch. 5.2 - Prob. 4E Ch. 5.2 - Prob. 5E Ch. 5.2 - Prob. 6E Ch. 5.2 - Prob. 7E Ch. 5.2 - Prob. 8E Ch. 5.2 - Prob. 9E Ch. 5.2 - Prob. 10E Ch. 5.2 - Prob. 11E Ch. 5.2 - Prob. 12E Ch. 5.2 - Prob. 13E Ch. 5.2 - Prob. 14E Ch. 5.2 - Prob. 15E Ch. 5.2 - Prob. 16E Ch. 5.2 - Prob. 17E Ch. 5.2 - Prob. 18E Ch. 5.2 - Prob. 19E Ch. 5.2 - Prob. 20E Ch. 5.2 - Prob. 21E Ch. 5.2 - Prob. 22E Ch. 5.2 - Prob. 23E Ch. 5.2 - Prob. 24E Ch. 5.2 - Prob. 25E Ch. 5.2 - Prob. 26E Ch. 5.2 - Prob. 27E Ch. 5.2 - Prob. 28E Ch. 5.2 - Prob. 29E Ch. 5.2 - Prob. 30E Ch. 5.2 - Prob. 31E Ch. 5.2 - Prob. 32E Ch. 5.2 - Prob. 33E Ch. 5.2 - Prob. 34E Ch. 5.2 - Prob. 35E Ch. 5.2 - Prob. 36E Ch. 5.2 - Prob. 37E Ch. 5.2 - Prob. 38E Ch. 5.2 - Prob. 39E Ch. 5.2 - Prob. 40E Ch. 5.2 - Prob. 41E Ch. 5.2 - Prob. 42E Ch. 5.2 - Prob. 43E Ch. 5.2 - Prob. 44E Ch. 5.2 - Prob. 45E Ch. 5.2 - Prob. 46E Ch. 5.2 - Prob. 47E Ch. 5.2 - Prob. 48E Ch. 5.2 - Prob. 49E Ch. 5.2 - Prob. 50E Ch. 5.2 - Prob. 51E Ch. 5.2 - Prob. 52E Ch. 5.2 - Prob. 53E Ch. 5.2 - Prob. 54E Ch. 5.2 - Prob. 55E Ch. 5.2 - Prob. 56E Ch. 5.2 - Prob. 57E Ch. 5.2 - Prob. 58E Ch. 5.2 - Prob. 59E Ch. 5.2 - Prob. 60E Ch. 5.2 - Prob. 61E Ch. 5.2 - Prob. 62E Ch. 5.2 - Prob. 63E Ch. 5.2 - Prob. 64E Ch. 5.2 - Prob. 65E Ch. 5.2 - Prob. 66E Ch. 5.2 - Prob. 67E Ch. 5.2 - Prob. 68E Ch. 5.2 - Prob. 69E Ch. 5.2 - Prob. 70E Ch. 5.2 - Prob. 71E Ch. 5.2 - Prob. 72E Ch. 5.2 - Prob. 73E Ch. 5.2 - Prob. 74E Ch. 5.3 - Prob. 1E Ch. 5.3 - Prob. 2E Ch. 5.3 - Prob. 3E Ch. 5.3 - Prob. 4E Ch. 5.3 - Prob. 5E Ch. 5.3 - Prob. 6E Ch. 5.3 - Prob. 7E Ch. 5.3 - Prob. 8E Ch. 5.3 - Prob. 9E Ch. 5.3 - Prob. 10E Ch. 5.3 - Prob. 11E Ch. 5.3 - Prob. 12E Ch. 5.3 - Prob. 13E Ch. 5.3 - Prob. 14E Ch. 5.3 - Prob. 15E Ch. 5.3 - Prob. 16E Ch. 5.3 - Prob. 17E Ch. 5.3 - Prob. 18E Ch. 5.3 - Prob. 19E Ch. 5.3 - Prob. 20E Ch. 5.3 - Prob. 21E Ch. 5.3 - Prob. 22E Ch. 5.3 - Prob. 23E Ch. 5.3 - Prob. 24E Ch. 5.3 - Prob. 25E Ch. 5.3 - Prob. 26E Ch. 5.3 - Prob. 27E Ch. 5.3 - Prob. 28E Ch. 5.3 - Prob. 29E Ch. 5.3 - Prob. 30E Ch. 5.3 - Prob. 31E Ch. 5.3 - Prob. 32E Ch. 5.3 - Prob. 33E Ch. 5.3 - Prob. 34E Ch. 5.3 - Prob. 35E Ch. 5.3 - Prob. 36E Ch. 5.3 - Prob. 37E Ch. 5.3 - Prob. 38E Ch. 5.3 - Prob. 39E Ch. 5.3 - Prob. 40E Ch. 5.3 - Prob. 41E Ch. 5.3 - Prob. 42E Ch. 5.3 - Prob. 43E Ch. 5.3 - Prob. 44E Ch. 5.3 - Prob. 45E Ch. 5.3 - Prob. 46E Ch. 5.3 - Prob. 47E Ch. 5.3 - Prob. 48E Ch. 5.3 - Prob. 49E Ch. 5.3 - Prob. 50E Ch. 5.3 - Prob. 51E Ch. 5.3 - Prob. 52E Ch. 5.3 - Prob. 53E Ch. 5.3 - Prob. 54E Ch. 5.3 - Prob. 55E Ch. 5.3 - Prob. 56E Ch. 5.3 - Prob. 57E Ch. 5.3 - Prob. 58E Ch. 5.3 - Prob. 59E Ch. 5.3 - Prob. 60E Ch. 5.3 - Prob. 61E Ch. 5.3 - Prob. 62E Ch. 5.3 - Prob. 63E Ch. 5.3 - Prob. 64E Ch. 5.3 - Prob. 65E Ch. 5.3 - Prob. 66E Ch. 5.3 - Prob. 67E Ch. 5.3 - Prob. 68E Ch. 5.3 - Prob. 69E Ch. 5.3 - Prob. 70E Ch. 5.3 - Prob. 71E Ch. 5.3 - Prob. 72E Ch. 5.3 - Prob. 73E Ch. 5.3 - Prob. 74E Ch. 5.3 - Prob. 75E Ch. 5.3 - Prob. 76E Ch. 5.3 - Prob. 77E Ch. 5.3 - Prob. 78E Ch. 5.3 - Prob. 79E Ch. 5.3 - Prob. 80E Ch. 5.3 - Prob. 81E Ch. 5.3 - Prob. 82E Ch. 5.3 - Prob. 83E Ch. 5.3 - Prob. 84E Ch. 5.3 - Prob. 85E Ch. 5.3 - Prob. 86E Ch. 5.3 - Prob. 87E Ch. 5.3 - Prob. 88E Ch. 5.3 - Prob. 89E Ch. 5.3 - Prob. 90E Ch. 5.3 - Prob. 91E Ch. 5.3 - Prob. 92E Ch. 5.3 - Prob. 93E Ch. 5.3 - Prob. 94E Ch. 5.3 - Prob. 95E Ch. 5.3 - Prob. 96E Ch. 5.3 - Prob. 97E Ch. 5.3 - Prob. 98E Ch. 5.3 - Prob. 99E Ch. 5.3 - Prob. 100E Ch. 5.3 - Prob. 101E Ch. 5.3 - Prob. 102E Ch. 5.3 - Prob. 103E Ch. 5.3 - Prob. 104E Ch. 5.4 - Prob. 1E Ch. 5.4 - Prob. 2E Ch. 5.4 - Prob. 3E Ch. 5.4 - Prob. 4E Ch. 5.4 - Prob. 5E Ch. 5.4 - Prob. 6E Ch. 5.4 - Prob. 7E Ch. 5.4 - Prob. 8E Ch. 5.4 - Prob. 9E Ch. 5.4 - Prob. 10E Ch. 5.4 - Prob. 11E Ch. 5.4 - Prob. 12E Ch. 5.4 - Prob. 13E Ch. 5.4 - Prob. 14E Ch. 5.4 - Prob. 15E Ch. 5.4 - Prob. 16E Ch. 5.4 - Prob. 17E Ch. 5.4 - Prob. 18E Ch. 5.4 - Prob. 19E Ch. 5.4 - Prob. 20E Ch. 5.4 - Prob. 21E Ch. 5.4 - Prob. 22E Ch. 5.4 - Prob. 23E Ch. 5.4 - Prob. 24E Ch. 5.4 - Prob. 25E Ch. 5.4 - Prob. 26E Ch. 5.4 - Prob. 27E Ch. 5.4 - Prob. 28E Ch. 5.4 - Prob. 29E Ch. 5.4 - Prob. 30E Ch. 5.4 - Prob. 31E Ch. 5.4 - Prob. 32E Ch. 5.4 - Prob. 33E Ch. 5.4 - Prob. 34E Ch. 5.4 - Prob. 35E Ch. 5.4 - Prob. 36E Ch. 5.4 - Prob. 37E Ch. 5.4 - Prob. 38E Ch. 5.4 - Prob. 39E Ch. 5.4 - Prob. 40E Ch. 5.4 - Prob. 41E Ch. 5.4 - Prob. 42E Ch. 5.4 - Prob. 43E Ch. 5.4 - Prob. 44E Ch. 5.4 - Prob. 45E Ch. 5.4 - Prob. 46E Ch. 5.4 - Prob. 47E Ch. 5.4 - Prob. 48E Ch. 5.4 - Prob. 49E Ch. 5.4 - Prob. 50E Ch. 5.4 - Prob. 51E Ch. 5.4 - Prob. 52E Ch. 5.4 - Prob. 53E Ch. 5.4 - Prob. 54E Ch. 5.4 - Prob. 55E Ch. 5.4 - Prob. 56E Ch. 5.4 - Prob. 57E Ch. 5.4 - Prob. 58E Ch. 5.4 - Prob. 59E Ch. 5.4 - Prob. 60E Ch. 5.4 - Prob. 61E Ch. 5.4 - Prob. 62E Ch. 5.4 - Prob. 63E Ch. 5.4 - Prob. 64E Ch. 5.4 - Prob. 65E Ch. 5.4 - Prob. 66E Ch. 5.4 - Prob. 67E Ch. 5.4 - Prob. 68E Ch. 5.4 - Prob. 69E Ch. 5.4 - Prob. 70E Ch. 5.4 - Prob. 71E Ch. 5.4 - Prob. 72E Ch. 5.4 - Prob. 73E Ch. 5.4 - Prob. 74E Ch. 5.4 - Prob. 75E Ch. 5.4 - Prob. 76E Ch. 5.4 - Prob. 77E Ch. 5.4 - Prob. 78E Ch. 5.4 - Prob. 79E Ch. 5.4 - Prob. 80E Ch. 5.4 - Prob. 81E Ch. 5.4 - Prob. 82E Ch. 5.4 - Prob. 83E Ch. 5.4 - Prob. 84E Ch. 5.4 - Prob. 85E Ch. 5.4 - Prob. 86E Ch. 5.4 - Prob. 87E Ch. 5.4 - Prob. 88E Ch. 5.4 - Prob. 89E Ch. 5.4 - Prob. 90E Ch. 5.4 - Prob. 91E Ch. 5.4 - Prob. 92E Ch. 5.4 - Prob. 93E Ch. 5.4 - Prob. 94E Ch. 5.4 - Prob. 95E Ch. 5.4 - Prob. 96E Ch. 5.4 - Prob. 97E Ch. 5.4 - Prob. 98E Ch. 5.4 - Prob. 99E Ch. 5.4 - Prob. 100E Ch. 5.4 - Prob. 101E Ch. 5.5 - Prob. 1E Ch. 5.5 - Prob. 2E Ch. 5.5 - Prob. 3E Ch. 5.5 - Prob. 4E Ch. 5.5 - Prob. 5E Ch. 5.5 - Prob. 6E Ch. 5.5 - Prob. 7E Ch. 5.5 - Prob. 8E Ch. 5.5 - Prob. 9E Ch. 5.5 - Prob. 10E Ch. 5.5 - Prob. 11E Ch. 5.5 - Prob. 12E Ch. 5.5 - Prob. 13E Ch. 5.5 - Prob. 14E Ch. 5.5 - Prob. 15E Ch. 5.5 - Prob. 16E Ch. 5.5 - Prob. 17E Ch. 5.5 - Prob. 18E Ch. 5.5 - Prob. 19E Ch. 5.5 - Prob. 20E Ch. 5.5 - Prob. 21E Ch. 5.5 - Prob. 22E Ch. 5.5 - Prob. 23E Ch. 5.5 - Prob. 24E Ch. 5.5 - Prob. 25E Ch. 5.5 - Prob. 26E Ch. 5.5 - Prob. 27E Ch. 5.5 - Prob. 28E Ch. 5.5 - Prob. 29E Ch. 5.5 - Prob. 30E Ch. 5.5 - Prob. 31E Ch. 5.5 - Prob. 32E Ch. 5.5 - Prob. 33E Ch. 5.5 - Prob. 34E Ch. 5.5 - Prob. 35E Ch. 5.5 - Prob. 36E Ch. 5.5 - Prob. 37E Ch. 5.5 - Prob. 38E Ch. 5.5 - Prob. 39E Ch. 5.5 - Prob. 40E Ch. 5.5 - Prob. 41E Ch. 5.5 - Prob. 42E Ch. 5.5 - Prob. 43E Ch. 5.5 - Prob. 44E Ch. 5.5 - Prob. 45E Ch. 5.5 - Prob. 46E Ch. 5.5 - Prob. 47E Ch. 5.5 - Prob. 48E Ch. 5.5 - Prob. 49E Ch. 5.5 - Prob. 50E Ch. 5.5 - Prob. 51E Ch. 5.5 - Prob. 52E Ch. 5.5 - Prob. 53E Ch. 5.5 - Prob. 54E Ch. 5.5 - Prob. 55E Ch. 5.5 - Prob. 56E Ch. 5.5 - Prob. 57E Ch. 5.5 - Prob. 58E Ch. 5.5 - Prob. 59E Ch. 5.5 - Prob. 60E Ch. 5.5 - Prob. 61E Ch. 5.5 - Prob. 62E Ch. 5.5 - Prob. 63E Ch. 5.5 - Prob. 64E Ch. 5.5 - Prob. 65E Ch. 5.5 - Prob. 66E Ch. 5.5 - Prob. 67E Ch. 5.5 - Prob. 68E Ch. 5.5 - Prob. 69E Ch. 5.5 - Prob. 70E Ch. 5.5 - Prob. 71E Ch. 5.5 - Prob. 72E Ch. 5.5 - Prob. 73E Ch. 5.5 - Prob. 74E Ch. 5.5 - Prob. 75E Ch. 5.5 - Prob. 76E Ch. 5.5 - Prob. 77E Ch. 5.5 - Prob. 78E Ch. 5.5 - Prob. 79E Ch. 5 - Prob. 1RE Ch. 5 - Prob. 2RE Ch. 5 - Prob. 3RE Ch. 5 - Prob. 4RE Ch. 5 - Prob. 5RE Ch. 5 - Prob. 6RE Ch. 5 - Prob. 7RE Ch. 5 - Prob. 8RE Ch. 5 - Prob. 9RE Ch. 5 - Prob. 10RE Ch. 5 - Prob. 11RE Ch. 5 - Prob. 12RE Ch. 5 - Prob. 13RE Ch. 5 - Prob. 14RE Ch. 5 - Prob. 15RE Ch. 5 - Prob. 16RE Ch. 5 - Prob. 17RE Ch. 5 - Prob. 18RE Ch. 5 - Prob. 19RE Ch. 5 - Prob. 20RE Ch. 5 - Prob. 21RE Ch. 5 - Prob. 22RE Ch. 5 - Prob. 23RE Ch. 5 - Prob. 24RE Ch. 5 - Prob. 25RE Ch. 5 - Prob. 26RE Ch. 5 - Prob. 27RE Ch. 5 - Prob. 28RE Ch. 5 - Prob. 29RE Ch. 5 - Prob. 30RE Ch. 5 - Prob. 31RE Ch. 5 - Prob. 32RE Ch. 5 - Prob. 33RE Ch. 5 - Prob. 34RE Ch. 5 - Prob. 35RE Ch. 5 - Prob. 36RE Ch. 5 - Prob. 37RE Ch. 5 - Prob. 38RE Ch. 5 - Prob. 39RE Ch. 5 - Prob. 40RE Ch. 5 - Prob. 41RE Ch. 5 - Prob. 42RE Ch. 5 - Prob. 43RE Ch. 5 - Prob. 44RE Ch. 5 - Prob. 45RE Ch. 5 - Prob. 46RE Ch. 5 - Prob. 47RE Ch. 5 - Prob. 48RE Ch. 5 - Prob. 49RE Ch. 5 - Prob. 50RE Ch. 5 - Prob. 51RE Ch. 5 - Prob. 52RE Ch. 5 - Prob. 53RE Ch. 5 - Prob. 54RE Ch. 5 - Prob. 55RE Ch. 5 - Prob. 56RE Ch. 5 - Prob. 57RE Ch. 5 - Prob. 58RE Ch. 5 - Prob. 59RE Ch. 5 - Prob. 60RE Ch. 5 - Prob. 61RE Ch. 5 - Prob. 62RE Ch. 5 - Prob. 63RE Ch. 5 - Prob. 64RE Ch. 5 - Prob. 65RE Ch. 5 - Prob. 66RE Ch. 5 - Prob. 67RE Ch. 5 - Prob. 68RE Ch. 5 - Prob. 69RE Ch. 5 - Prob. 70RE Ch. 5 - Prob. 71RE Ch. 5 - Prob. 72RE Ch. 5 - Prob. 73RE Ch. 5 - Prob. 74RE Ch. 5 - Prob. 75RE Ch. 5 - Prob. 76RE Ch. 5 - Prob. 77RE Ch. 5 - Prob. 78RE Ch. 5 - Prob. 79RE Ch. 5 - Prob. 80RE Ch. 5 - Prob. 81RE Ch. 5 - Prob. 82RE Ch. 5 - Prob. 83RE Ch. 5 - Prob. 84RE Ch. 5 - Prob. 85RE Ch. 5 - Prob. 1CT Ch. 5 - Prob. 2CT Ch. 5 - Prob. 3CT Ch. 5 - Prob. 4CT Ch. 5 - Prob. 5CT Ch. 5 - Prob. 6CT Ch. 5 - Prob. 7CT Ch. 5 - Prob. 8CT Ch. 5 - Prob. 9CT Ch. 5 - Prob. 10CT Ch. 5 - Prob. 11CT Ch. 5 - Prob. 12CT Ch. 5 - Prob. 13CT Ch. 5 - Prob. 14CT Ch. 5 - Prob. 15CT Ch. 5 - Prob. 16CT Ch. 5 - Prob. 17CT Ch. 5 - Prob. 18CT Ch. 5 - Prob. 19CT Ch. 5 - Prob. 20CT Ch. 5 - Prob. 21CT Ch. 5 - Prob. 22CT Ch. 5 - Prob. 23CT Ch. 5 - Prob. 24CT Ch. 5 - Prob. 25CT Ch. 5 - Prob. 1PS Ch. 5 - Prob. 2PS Ch. 5 - Prob. 3PS Ch. 5 - Prob. 4PS Ch. 5 - Prob. 5PS Ch. 5 - Prob. 6PS Ch. 5 - Prob. 7PS Ch. 5 - Prob. 8PS Ch. 5 - Prob. 9PS Ch. 5 - Prob. 10PS Ch. 5 - Prob. 11PS Ch. 5 - Prob. 12PS Ch. 5 - Prob. 13PS Ch. 5 - Prob. 14PS Ch. 5 - Prob. 15PS Ch. 5 - Prob. 16PS

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.