
Concept explainers
Unsanitary Restaurants
Health officials routinely check the sanitary condition of restaurants. Assume you visit a popular tourist spot and read in the newspaper that in 3 out of every 7 restaurants checked, unsatisfactory health conditions were found. Assuming you are planning to eat out 10 times while you are there on vacation, answer the following questions.
1. How likely is it that you will eat at three restaurants with unsanitary conditions?
2. How likely is it that you will eat at four or five restaurants with unsanitary conditions?
3. Explain how you would compute the
4. What is the most likely number to occur in this experiment?
5. How variable will the data be around the most likely number?
6. How do you know that this is a binomial distribution?
7. If it is a binomial distribution, does that
Mean = 4.29 Std. dev. = 1.56492
| X | P(X) | Cum. prob. |
| 0 | 0.00371 | 0.00371 |
| 1 | 0.02784 | 0.03155 |
| 2 | 0.09396 | 0.12552 |
| 3 | 0.18793 | 0.31344 |
| 4 | 0.24665 | 0.56009 |
| 5 | 0.22199 | 0.78208 |
| 6 | 0.13874 | 0.92082 |
| 7 | 0.05946 | 0.98028 |
| 8 | 0.01672 | 0.99700 |
| 9 | 0.00279 | 0.99979 |
| 10 | 0.00021 | 1.00000 |
a.
The probability that the person is likely to eat at all three restaurants with unsanitary conditions.
Answer to Problem 1AC
The probability the person is likely to eat at all three restaurants with unsanitary conditions is 0.186.
Explanation of Solution
Given info:
A person is planning to eat outside 10 times during a vacation. Health officials checks the sanitary condition of restaurant and found that every 3 out of 7 restaurants checked was having an unsatisfactory health conditions.
Calculation:
Define the random variable x as the number of restaurants with unsanitary conditions. Here, the total number of restaurants are (n) is 10 and each restaurant is independent from other restaurants. Also, there are two possible outcomes (having an unsanitary conditions or didn’t have an unsanitary conditions) and the probability of that the selected restaurant having an unsanitary conditions gives the probability (p)
The binomial distribution formula is,
Where, n is the number of trials, x is the number of successes among n trials, p is the probability of success and q is the probability of failure.
Substitute n as 10, p as 0.43, q as
Thus, the probability the person is likely to eat at all three restaurants with unsanitary conditions is 0.186.
b.
The probability that the person is likely to eat at four or five restaurants with unsanitary conditions.
Answer to Problem 1AC
The probability the person is likely to eat at four or five restaurants with unsanitary conditions is 0.469.
Explanation of Solution
Here, “Eating at four or five restaurants with unsanitary conditions gives the values of X as 4 and 5.
Substitute n as 10, p as 0.43, q as
Thus, the probability the person is likely to eat at four or five restaurants with unsanitary conditions is 0.469.
c.
To explain: The way to compute the probability of eating in at least one restaurant with unsanitary conditions.
To find: The probability of eating in at least one restaurant with unsanitary conditions.
Answer to Problem 1AC
The way to compute the probability of eating in at least one restaurant with unsanitary conditions is given below:
Eating in at least one restaurant is same as eating in 1 or more than 1 restaurants.
The probability of eating in at least one restaurant with unsanitary conditions is 0.9964.
Explanation of Solution
Calculation:
Substitute n as 10, p as 0.43, q as
=0.9964
Thus, the probability of eating in at least one restaurant is 0.9964.
d.
The most likely number that could occur in the given experiment.
Answer to Problem 1AC
The most likely number that could occur in the given experiment is the event of eating in 4 restaurants with unsanitary conditions.
Explanation of Solution
Calculation:
Software procedure:
Software procedure for calculating the probability is given below:
- Choose Calc > Probability Distributions > Binomial Distribution.
- Choose Probability.
- Enter Number of trials as 10 and Event probability as 0.43.
- In Input columns, enter the column containing the values 0, 1, 2, 3,…10.
- Click OK.
Output obtained from MINITAB is given below:
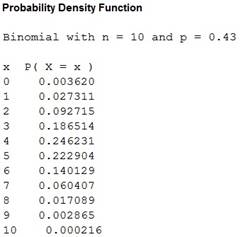
Justification:
From the MINITAB output it can be observed that the probability of eating in 4 restaurants has the highest probability of 0.2462.
The probability for 4 restaurants is the highest, but the expected number of restaurants that a person would eat is
e.
To find: The variability of the data around the most likely number.
Answer to Problem 1AC
The variability of the data around the most likely number would be 1.565 restaurants.
Explanation of Solution
Calculation:
Standard deviation:
Substitute n as 10, p as 0.43 and q as
Thus, the variability of the data around the most likely number would be 1.565 restaurants.
f.
To justify: The reason for identifying the given experiment as binomial.
Answer to Problem 1AC
The given experiment satisfies all the “requirements of binomial distribution”.
Explanation of Solution
Justification:
Requirements of binomial distribution:
- There will be a fixed number of trials.
- There are only two possible outcomes (success and failure).
- The probability of success remains constant.
- The outcomes obtained from each trial are independent of one another.
Here, the number of restaurants is 10 and it gives the fixed number of trials, there are only two possible outcomes either a restaurant might have unsanitary condition or a restaurant might not have unsanitary condition. The probability of that the selected restaurant having an unsanitary conditions gives the probability (p)
Thus, the given experiment is a binomial distribution.
g.
To check: Whether the mean of the likelihood of success is always 50%.
Answer to Problem 1AC
The mean of the likelihood of success will vary from situation to situation.
Explanation of Solution
Given info:
Use the computer generated table for checking.
Justification:
In binomial distribution the probability of success remains constant and it is 50% but it varies for situation to situation. Just having two outcomes will not assurance for equal probabilities of success.
Want to see more full solutions like this?
Chapter 5 Solutions
Elementary Statistics: A Step By Step Approach
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Introductory Statistics
Precalculus: A Unit Circle Approach (3rd Edition)
College Algebra (Collegiate Math)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Thinking Mathematically (6th Edition)
- At the same restaurant as in Question 19 with the same normal distribution, what's the chance of it taking no more than 15 minutes to get service?arrow_forwardClint, obviously not in college, sleeps an average of 8 hours per night with a standard deviation of 15 minutes. What's the chance of him sleeping between 7.5 and 8.5 hours on any given night? 0-(7-0) 200 91109s and doiw $20 (8-0) mol 8520 slang $199 galbrog seam side pide & D (newid se od poyesvig as PELEO PER AFTE editiw noudab temand van Czarrow_forwardTimes to complete a statistics exam have a normal distribution with a mean of 40 minutes and standard deviation of 6 minutes. Deshawn's time comes in at the 90th percentile. What percentage of the students are still working on their exams when Deshawn leaves?arrow_forward
- Suppose that the weights of cereal boxes have a normal distribution with a mean of 20 ounces and standard deviation of half an ounce. A box that has a standard score of o weighs how much? syed by ilog ni 21arrow_forwardBob scores 80 on both his math exam (which has a mean of 70 and standard deviation of 10) and his English exam (which has a mean of 85 and standard deviation of 5). Find and interpret Bob's Z-scores on both exams to let him know which exam (if either) he did bet- ter on. Don't, however, let his parents know; let them think he's just as good at both subjects. algas 70) sering digarrow_forwardSue's math class exam has a mean of 70 with a standard deviation of 5. Her standard score is-2. What's her original exam score?arrow_forward
- Clint sleeps an average of 8 hours per night with a standard deviation of 15 minutes. What's the chance he will sleep less than 7.5 hours tonight? nut bow visarrow_forwardSuppose that your score on an exam is directly at the mean. What's your standard score?arrow_forwardOne state's annual rainfall has a normal dis- tribution with a mean of 100 inches and standard deviation of 25 inches. Suppose that corn grows best when the annual rainfall is between 100 and 150 inches. What's the chance of achieving this amount of rainfall? wved now of sociarrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





