Glencoe Geometry Student Edition C2014
1st Edition
ISBN: 9780076639298
Author: Glencoe Mcgraw-Hill
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 5.2, Problem 42HP
a.
To determine
ToDraw:An acute
a.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An acute triangle whose all three
Below is figure of acute triangle.
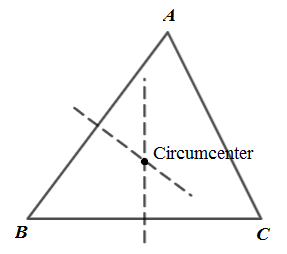
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
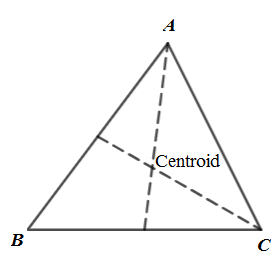
Centroid: It is intersection of medians of triangle. As shown in below figure.
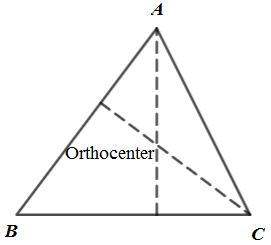
Orthocenter: It is intersetion point of altitudes of a triangle.
b.
To determine
To Draw: An obstude triangle and find the circumcenter, centroid and orthocenter.
b.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An obtude triangle whose one angle is obtuse. An obtude angle is greater than
Below is figure of obtuse triangle.
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
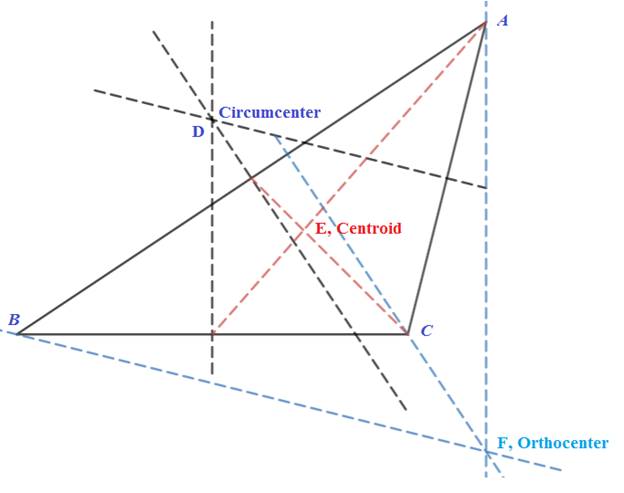
c.
To determine
To Draw:Anright triangle and find the circumcenter, centroid and orthocenter.
c.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An right triangle whose one angle is right.
Below is figure of right triangle.
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
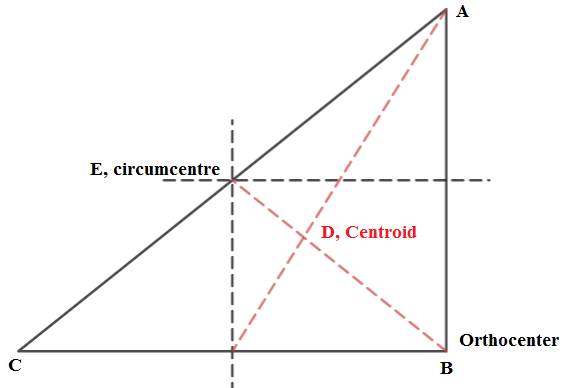
d.
To determine
To explain:The conjecture of all three centers.
d.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
In acute triangle all three centre lie inside the triangle.
In obtuse triangle orthocenter and circumcenter lie outside the triangle. Centroid lie inside the triangle.
In right triangle circumcenter lie on hypotenuse and orthocenter is opposite vertex of hypotenuse of triangle. Centroid lie inside the triangle.
Chapter 5 Solutions
Glencoe Geometry Student Edition C2014
Ch. 5.1 - Prob. 1ACYPCh. 5.1 - Prob. 1BCYPCh. 5.1 - Prob. 1CCYPCh. 5.1 - Prob. 2CYPCh. 5.1 - Prob. 3ACYPCh. 5.1 - Prob. 3BCYPCh. 5.1 - Prob. 3CCYPCh. 5.1 - Prob. 4ACYPCh. 5.1 - Prob. 4BCYPCh. 5.1 - Prob. 1CYU
Ch. 5.1 - Prob. 2CYUCh. 5.1 - Prob. 3CYUCh. 5.1 - Prob. 4CYUCh. 5.1 - Prob. 5CYUCh. 5.1 - Prob. 6CYUCh. 5.1 - Prob. 7CYUCh. 5.1 - Prob. 8CYUCh. 5.1 - Prob. 9PPSCh. 5.1 - Prob. 10PPSCh. 5.1 - Prob. 11PPSCh. 5.1 - Prob. 12PPSCh. 5.1 - Prob. 13PPSCh. 5.1 - Prob. 14PPSCh. 5.1 - Prob. 15PPSCh. 5.1 - Prob. 16PPSCh. 5.1 - Prob. 17PPSCh. 5.1 - Prob. 18PPSCh. 5.1 - Prob. 19PPSCh. 5.1 - Prob. 20PPSCh. 5.1 - Prob. 21PPSCh. 5.1 - Prob. 22PPSCh. 5.1 - Prob. 23PPSCh. 5.1 - Prob. 24PPSCh. 5.1 - Prob. 25PPSCh. 5.1 - Prob. 26PPSCh. 5.1 - Prob. 27PPSCh. 5.1 - Prob. 28PPSCh. 5.1 - Prob. 29PPSCh. 5.1 - Prob. 30PPSCh. 5.1 - Prob. 31PPSCh. 5.1 - Prob. 32PPSCh. 5.1 - Prob. 33PPSCh. 5.1 - Prob. 34PPSCh. 5.1 - Prob. 35PPSCh. 5.1 - Prob. 36PPSCh. 5.1 - Prob. 37PPSCh. 5.1 - Prob. 38PPSCh. 5.1 - Prob. 39PPSCh. 5.1 - Prob. 40PPSCh. 5.1 - Prob. 41PPSCh. 5.1 - Prob. 42PPSCh. 5.1 - Prob. 43PPSCh. 5.1 - Prob. 44PPSCh. 5.1 - Prob. 45PPSCh. 5.1 - Prob. 46PPSCh. 5.1 - Prob. 47PPSCh. 5.1 - Prob. 48HPCh. 5.1 - Prob. 49HPCh. 5.1 - Prob. 50HPCh. 5.1 - Prob. 51HPCh. 5.1 - Prob. 52HPCh. 5.1 - Prob. 53HPCh. 5.1 - Prob. 54HPCh. 5.1 - Prob. 55STPCh. 5.1 - Prob. 56STPCh. 5.1 - Prob. 57STPCh. 5.1 - Prob. 58STPCh. 5.1 - Prob. 59SPRCh. 5.1 - Prob. 60SPRCh. 5.1 - Prob. 61SPRCh. 5.1 - Prob. 62SPRCh. 5.1 - Prob. 63SPRCh. 5.1 - Prob. 64SPRCh. 5.1 - Prob. 65SPRCh. 5.1 - Prob. 66SPRCh. 5.1 - Prob. 67SPRCh. 5.1 - Prob. 68SRCh. 5.1 - Prob. 69SRCh. 5.2 - Prob. 1ACYPCh. 5.2 - Prob. 1BCYPCh. 5.2 - Prob. 2ACYPCh. 5.2 - Prob. 2BCYPCh. 5.2 - Prob. 3CYPCh. 5.2 - Prob. 4CYPCh. 5.2 - Prob. 1CYUCh. 5.2 - Prob. 2CYUCh. 5.2 - Prob. 3CYUCh. 5.2 - Prob. 4CYUCh. 5.2 - Prob. 5PPSCh. 5.2 - Prob. 6PPSCh. 5.2 - Prob. 7PPSCh. 5.2 - Prob. 8PPSCh. 5.2 - Prob. 9PPSCh. 5.2 - Prob. 10PPSCh. 5.2 - Prob. 11PPSCh. 5.2 - Prob. 12PPSCh. 5.2 - Prob. 13PPSCh. 5.2 - Prob. 14PPSCh. 5.2 - Prob. 15PPSCh. 5.2 - Prob. 16PPSCh. 5.2 - Prob. 17PPSCh. 5.2 - Prob. 18PPSCh. 5.2 - Prob. 19PPSCh. 5.2 - Prob. 20PPSCh. 5.2 - Prob. 21PPSCh. 5.2 - Prob. 22PPSCh. 5.2 - Prob. 23PPSCh. 5.2 - Prob. 24PPSCh. 5.2 - Prob. 25PPSCh. 5.2 - Prob. 26PPSCh. 5.2 - Prob. 27PPSCh. 5.2 - Prob. 28PPSCh. 5.2 - Prob. 29PPSCh. 5.2 - Prob. 30PPSCh. 5.2 - Prob. 31PPSCh. 5.2 - Prob. 32PPSCh. 5.2 - Prob. 33PPSCh. 5.2 - Prob. 34PPSCh. 5.2 - Prob. 35PPSCh. 5.2 - Prob. 36PPSCh. 5.2 - Prob. 37HPCh. 5.2 - Prob. 38HPCh. 5.2 - Prob. 39HPCh. 5.2 - Prob. 40HPCh. 5.2 - Prob. 41HPCh. 5.2 - Prob. 42HPCh. 5.2 - Prob. 43HPCh. 5.2 - Prob. 44STPCh. 5.2 - Prob. 45STPCh. 5.2 - Prob. 46STPCh. 5.2 - Prob. 47STPCh. 5.2 - Prob. 48SPRCh. 5.2 - Prob. 49SPRCh. 5.2 - Prob. 50SPRCh. 5.2 - Prob. 51SPRCh. 5.2 - Prob. 52SPRCh. 5.2 - Prob. 53SPRCh. 5.2 - Prob. 54SPRCh. 5.2 - Prob. 55SPRCh. 5.2 - Prob. 56SRCh. 5.3 - Prob. 1ACYPCh. 5.3 - Prob. 1BCYPCh. 5.3 - Prob. 2CYPCh. 5.3 - Prob. 3CYPCh. 5.3 - Prob. 4CYPCh. 5.3 - Prob. 1CYUCh. 5.3 - Prob. 2CYUCh. 5.3 - Prob. 3CYUCh. 5.3 - Prob. 4CYUCh. 5.3 - Prob. 5CYUCh. 5.3 - Prob. 6CYUCh. 5.3 - Prob. 7CYUCh. 5.3 - Prob. 8PPSCh. 5.3 - Prob. 9PPSCh. 5.3 - Prob. 10PPSCh. 5.3 - Prob. 11PPSCh. 5.3 - Prob. 12PPSCh. 5.3 - Prob. 13PPSCh. 5.3 - Prob. 14PPSCh. 5.3 - Prob. 15PPSCh. 5.3 - Prob. 16PPSCh. 5.3 - Prob. 17PPSCh. 5.3 - Prob. 18PPSCh. 5.3 - Prob. 19PPSCh. 5.3 - Prob. 20PPSCh. 5.3 - Prob. 21PPSCh. 5.3 - Prob. 22PPSCh. 5.3 - Prob. 23PPSCh. 5.3 - Prob. 24PPSCh. 5.3 - Prob. 25PPSCh. 5.3 - Prob. 26PPSCh. 5.3 - Prob. 27PPSCh. 5.3 - Prob. 28PPSCh. 5.3 - Prob. 29PPSCh. 5.3 - Prob. 30PPSCh. 5.3 - Prob. 31PPSCh. 5.3 - Prob. 32PPSCh. 5.3 - Prob. 33PPSCh. 5.3 - Prob. 34PPSCh. 5.3 - Prob. 35PPSCh. 5.3 - Prob. 36PPSCh. 5.3 - Prob. 37PPSCh. 5.3 - Prob. 38PPSCh. 5.3 - Prob. 39PPSCh. 5.3 - Prob. 40PPSCh. 5.3 - Prob. 41PPSCh. 5.3 - Prob. 42PPSCh. 5.3 - Prob. 43HPCh. 5.3 - Prob. 44HPCh. 5.3 - Prob. 45HPCh. 5.3 - Prob. 46HPCh. 5.3 - Prob. 47HPCh. 5.3 - Prob. 48HPCh. 5.3 - Prob. 49STPCh. 5.3 - Prob. 50STPCh. 5.3 - Prob. 51STPCh. 5.3 - Prob. 52STPCh. 5.3 - Prob. 53SPRCh. 5.3 - Prob. 54SPRCh. 5.3 - Prob. 55SPRCh. 5.3 - Prob. 56SPRCh. 5.3 - Prob. 57SPRCh. 5.3 - Prob. 58SPRCh. 5.3 - Prob. 59SRCh. 5.3 - Prob. 60SRCh. 5.3 - Prob. 61SRCh. 5.4 - Prob. 1ACYPCh. 5.4 - Prob. 1BCYPCh. 5.4 - Prob. 1CCYPCh. 5.4 - Prob. 2ACYPCh. 5.4 - Prob. 2BCYPCh. 5.4 - Prob. 3CYPCh. 5.4 - Prob. 4CYPCh. 5.4 - Prob. 5CYPCh. 5.4 - Prob. 1CYUCh. 5.4 - Prob. 2CYUCh. 5.4 - Prob. 3CYUCh. 5.4 - Prob. 4CYUCh. 5.4 - Prob. 5CYUCh. 5.4 - Prob. 6CYUCh. 5.4 - Prob. 7CYUCh. 5.4 - Prob. 8CYUCh. 5.4 - Prob. 9CYUCh. 5.4 - Prob. 10CYUCh. 5.4 - Prob. 11PPSCh. 5.4 - Prob. 12PPSCh. 5.4 - Prob. 13PPSCh. 5.4 - Prob. 14PPSCh. 5.4 - Prob. 15PPSCh. 5.4 - Prob. 16PPSCh. 5.4 - Prob. 17PPSCh. 5.4 - Prob. 18PPSCh. 5.4 - Prob. 19PPSCh. 5.4 - Prob. 20PPSCh. 5.4 - Prob. 21PPSCh. 5.4 - Prob. 22PPSCh. 5.4 - Prob. 23PPSCh. 5.4 - Prob. 24PPSCh. 5.4 - Prob. 25PPSCh. 5.4 - Prob. 26PPSCh. 5.4 - Prob. 27PPSCh. 5.4 - Prob. 28PPSCh. 5.4 - Prob. 29PPSCh. 5.4 - Prob. 30PPSCh. 5.4 - Prob. 31PPSCh. 5.4 - Prob. 32PPSCh. 5.4 - Prob. 33PPSCh. 5.4 - Prob. 34PPSCh. 5.4 - Prob. 35PPSCh. 5.4 - Prob. 36PPSCh. 5.4 - Prob. 37PPSCh. 5.4 - Prob. 38PPSCh. 5.4 - Prob. 39PPSCh. 5.4 - Prob. 40HPCh. 5.4 - Prob. 41HPCh. 5.4 - Prob. 42HPCh. 5.4 - Prob. 43HPCh. 5.4 - Prob. 44HPCh. 5.4 - Prob. 45STPCh. 5.4 - Prob. 46STPCh. 5.4 - Prob. 47STPCh. 5.4 - Prob. 48STPCh. 5.4 - Prob. 49SPRCh. 5.4 - Prob. 50SPRCh. 5.4 - Prob. 51SPRCh. 5.4 - Prob. 52SPRCh. 5.4 - Prob. 53SPRCh. 5.4 - Prob. 54SPRCh. 5.4 - Prob. 55SPRCh. 5.4 - Prob. 56SPRCh. 5.4 - Prob. 57SRCh. 5.4 - Prob. 58SRCh. 5.4 - Prob. 59SRCh. 5.5 - Prob. 1ACYPCh. 5.5 - Prob. 1BCYPCh. 5.5 - Prob. 2CYPCh. 5.5 - Prob. 3CYPCh. 5.5 - Prob. 1CYUCh. 5.5 - Prob. 2CYUCh. 5.5 - Prob. 3CYUCh. 5.5 - Prob. 4CYUCh. 5.5 - Prob. 5CYUCh. 5.5 - Prob. 6PPSCh. 5.5 - Prob. 7PPSCh. 5.5 - Prob. 8PPSCh. 5.5 - Prob. 9PPSCh. 5.5 - Prob. 10PPSCh. 5.5 - Prob. 11PPSCh. 5.5 - Prob. 12PPSCh. 5.5 - Prob. 13PPSCh. 5.5 - Prob. 14PPSCh. 5.5 - Prob. 15PPSCh. 5.5 - Prob. 16PPSCh. 5.5 - Prob. 17PPSCh. 5.5 - Prob. 18PPSCh. 5.5 - Prob. 19PPSCh. 5.5 - Prob. 20PPSCh. 5.5 - Prob. 21PPSCh. 5.5 - Prob. 22PPSCh. 5.5 - Prob. 23PPSCh. 5.5 - Prob. 24PPSCh. 5.5 - Prob. 25PPSCh. 5.5 - Prob. 26PPSCh. 5.5 - Prob. 27PPSCh. 5.5 - Prob. 28PPSCh. 5.5 - Prob. 29PPSCh. 5.5 - Prob. 30PPSCh. 5.5 - Prob. 31PPSCh. 5.5 - Prob. 32PPSCh. 5.5 - Prob. 33PPSCh. 5.5 - Prob. 34PPSCh. 5.5 - Prob. 35PPSCh. 5.5 - Prob. 36PPSCh. 5.5 - Prob. 37PPSCh. 5.5 - Prob. 38PPSCh. 5.5 - Prob. 39PPSCh. 5.5 - Prob. 40PPSCh. 5.5 - Prob. 41PPSCh. 5.5 - Prob. 42PPSCh. 5.5 - Prob. 43HPCh. 5.5 - Prob. 44HPCh. 5.5 - Prob. 45HPCh. 5.5 - Prob. 46HPCh. 5.5 - Prob. 47HPCh. 5.5 - Prob. 48HPCh. 5.5 - Prob. 49STPCh. 5.5 - Prob. 50STPCh. 5.5 - Prob. 51STPCh. 5.5 - Prob. 52STPCh. 5.5 - Prob. 53SPRCh. 5.5 - Prob. 54SPRCh. 5.5 - Prob. 55SPRCh. 5.5 - Prob. 56SPRCh. 5.5 - Prob. 57SPRCh. 5.5 - Prob. 58SPRCh. 5.5 - Prob. 59SPRCh. 5.5 - Prob. 60SPRCh. 5.5 - Prob. 61SRCh. 5.5 - Prob. 62SRCh. 5.5 - Prob. 63SRCh. 5.6 - Prob. 1ACYPCh. 5.6 - Prob. 1BCYPCh. 5.6 - Prob. 2ACYPCh. 5.6 - Prob. 2BCYPCh. 5.6 - Prob. 3CYPCh. 5.6 - Prob. 4CYPCh. 5.6 - Prob. 5CYPCh. 5.6 - Prob. 1CYUCh. 5.6 - Prob. 2CYUCh. 5.6 - Prob. 3CYUCh. 5.6 - Prob. 4CYUCh. 5.6 - Prob. 5CYUCh. 5.6 - Prob. 6CYUCh. 5.6 - Prob. 7CYUCh. 5.6 - Prob. 8CYUCh. 5.6 - Prob. 9CYUCh. 5.6 - Prob. 10PPSCh. 5.6 - Prob. 11PPSCh. 5.6 - Prob. 12PPSCh. 5.6 - Prob. 13PPSCh. 5.6 - Prob. 14PPSCh. 5.6 - Prob. 15PPSCh. 5.6 - Prob. 16PPSCh. 5.6 - Prob. 17PPSCh. 5.6 - Prob. 18PPSCh. 5.6 - Prob. 19PPSCh. 5.6 - Prob. 20PPSCh. 5.6 - Prob. 21PPSCh. 5.6 - Prob. 22PPSCh. 5.6 - Prob. 23PPSCh. 5.6 - Prob. 24PPSCh. 5.6 - Prob. 25PPSCh. 5.6 - Prob. 26PPSCh. 5.6 - Prob. 27PPSCh. 5.6 - Prob. 28PPSCh. 5.6 - Prob. 29PPSCh. 5.6 - Prob. 30PPSCh. 5.6 - Prob. 31PPSCh. 5.6 - Prob. 32PPSCh. 5.6 - Prob. 33PPSCh. 5.6 - Prob. 34PPSCh. 5.6 - Prob. 35PPSCh. 5.6 - Prob. 36PPSCh. 5.6 - Prob. 37PPSCh. 5.6 - Prob. 38HPCh. 5.6 - Prob. 39HPCh. 5.6 - Prob. 40HPCh. 5.6 - Prob. 41HPCh. 5.6 - Prob. 42HPCh. 5.6 - Prob. 43STPCh. 5.6 - Prob. 44STPCh. 5.6 - Prob. 45STPCh. 5.6 - Prob. 46STPCh. 5.6 - Prob. 47SPRCh. 5.6 - Prob. 48SPRCh. 5.6 - Prob. 49SPRCh. 5.6 - Prob. 50SPRCh. 5.6 - Prob. 51SPRCh. 5.6 - Prob. 52SPRCh. 5.6 - Prob. 53SPRCh. 5.6 - Prob. 54SPRCh. 5.6 - Prob. 55SPRCh. 5.6 - Prob. 56SRCh. 5.6 - Prob. 57SRCh. 5.6 - Prob. 58SRCh. 5 - Prob. 1GRFCCh. 5 - Prob. 2GRFCCh. 5 - Prob. 3GRFCCh. 5 - Prob. 4GRFCCh. 5 - Prob. 5GRFCCh. 5 - Prob. 6GRFCCh. 5 - Prob. 7GRFCCh. 5 - Prob. 8GRFCCh. 5 - Prob. 9GRFCCh. 5 - Prob. 10GRFCCh. 5 - Prob. 11GRFCCh. 5 - Prob. 12GRFCCh. 5 - Prob. 1MCQCh. 5 - Prob. 2MCQCh. 5 - Prob. 3MCQCh. 5 - Prob. 4MCQCh. 5 - Prob. 5MCQCh. 5 - Prob. 6MCQCh. 5 - Prob. 7MCQCh. 5 - Prob. 8MCQCh. 5 - Prob. 9MCQCh. 5 - Prob. 10MCQCh. 5 - Prob. 11MCQCh. 5 - Prob. 12MCQCh. 5 - Prob. 13MCQCh. 5 - Prob. 14MCQCh. 5 - Prob. 15MCQCh. 5 - Prob. 16MCQCh. 5 - Prob. 17MCQCh. 5 - Prob. 18MCQCh. 5 - Prob. 19MCQCh. 5 - Prob. 1SGRCh. 5 - Prob. 2SGRCh. 5 - Prob. 3SGRCh. 5 - Prob. 4SGRCh. 5 - Prob. 5SGRCh. 5 - Prob. 6SGRCh. 5 - Prob. 7SGRCh. 5 - Prob. 8SGRCh. 5 - Prob. 9SGRCh. 5 - Prob. 10SGRCh. 5 - Prob. 11SGRCh. 5 - Prob. 12SGRCh. 5 - Prob. 13SGRCh. 5 - Prob. 14SGRCh. 5 - Prob. 15SGRCh. 5 - Prob. 16SGRCh. 5 - Prob. 17SGRCh. 5 - Prob. 18SGRCh. 5 - Prob. 19SGRCh. 5 - Prob. 20SGRCh. 5 - Prob. 21SGRCh. 5 - Prob. 22SGRCh. 5 - Prob. 23SGRCh. 5 - Prob. 24SGRCh. 5 - Prob. 25SGRCh. 5 - Prob. 26SGRCh. 5 - Prob. 27SGRCh. 5 - Prob. 28SGRCh. 5 - Prob. 29SGRCh. 5 - Prob. 30SGRCh. 5 - Prob. 31SGRCh. 5 - Prob. 32SGRCh. 5 - Prob. 33SGRCh. 5 - Prob. 1PTCh. 5 - Prob. 2PTCh. 5 - Prob. 3PTCh. 5 - Prob. 4PTCh. 5 - Prob. 5PTCh. 5 - Prob. 6PTCh. 5 - Prob. 7PTCh. 5 - Prob. 8PTCh. 5 - Prob. 9PTCh. 5 - Prob. 10PTCh. 5 - Prob. 11PTCh. 5 - Prob. 12PTCh. 5 - Prob. 13PTCh. 5 - Prob. 14PTCh. 5 - Prob. 15PTCh. 5 - Prob. 16PTCh. 5 - Prob. 17PTCh. 5 - Prob. 18PTCh. 5 - Prob. 19PTCh. 5 - Prob. 20PTCh. 5 - Prob. 21PTCh. 5 - Prob. 22PTCh. 5 - Prob. 23PTCh. 5 - Prob. 24PTCh. 5 - Prob. 25PTCh. 5 - Prob. 1ECh. 5 - Prob. 2ECh. 5 - Prob. 3ECh. 5 - Prob. 4ECh. 5 - Prob. 5ECh. 5 - Prob. 1STPCh. 5 - Prob. 2STPCh. 5 - Prob. 3STPCh. 5 - Prob. 4STPCh. 5 - Prob. 5STPCh. 5 - Prob. 6STPCh. 5 - Prob. 7STPCh. 5 - Prob. 8STPCh. 5 - Prob. 9STPCh. 5 - Prob. 10STPCh. 5 - Prob. 11STPCh. 5 - Prob. 12STPCh. 5 - Prob. 13STPCh. 5 - Prob. 14STPCh. 5 - Prob. 15STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...
Basic Business Statistics, Student Value Edition
CHECK POINT 1 Find a counterexample to show that the statement The product of two two-digit numbers is a three-...
Thinking Mathematically (6th Edition)
14. SAT Test When making a random guess for an answer to a multiple choice question on an SAT test, the possibl...
Elementary Statistics (13th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Views on Capital Punishment In carrying out a study of views on capital punishment, a student asked a question ...
Introductory Statistics
Mathematical Connections Explain why a number and a numeral are considered different.
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Please help me answer this question!. Please handwrite it. I don't require AI answers. Thanks for your time!.arrow_forward1 What is the area of triangle ABC? 12 60° 60° A D B A 6√√3 square units B 18√3 square units 36√3 square units D 72√3 square unitsarrow_forwardPar quel quadrilatère est-elle représentée sur ce besoin en perspective cavalièrearrow_forward
- -10 M 10 y 5 P -5 R 5 -5 Ο 10 N -10 Οarrow_forwardDescribe enlargement on map gridarrow_forward◆ Switch To Light Mode HOMEWORK: 18, 19, 24, 27, 29 ***Please refer to the HOMEWORK sheet from Thursday, 9/14, for the problems ****Please text or email me if you have any questions 18. Figure 5-35 is a map of downtown Royalton, showing the Royalton River running through the downtown area and the three islands (A, B, and C) connected to each other and both banks by eight bridges. The Down- town Athletic Club wants to design the route for a marathon through the downtown area. Draw a graph that models the layout of Royalton. FIGURE 5-35 North Royalton Royalton River South Royption 19. A night watchman must walk the streets of the Green Hills subdivision shown in Fig. 5-36. The night watch- man needs to walk only once along each block. Draw a graph that models this situation.arrow_forward
- Solve this question and check if my answer provided is correctarrow_forwardProof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forwardQuadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forward
- An angle measures 70.6° more than the measure of its supplementary angle. What is the measure of each angle?arrow_forwardName: Date: Per: Unit 7: Geometry Homework 4: Parallel Lines & Transversals **This is a 2-page document! ** Directions: Classify each angle pair and indicate whether they are congruent or supplementary. 1 1.23 and 25 2. 24 and 28 3. 22 and 25 4. 22 and 28 5. 21 and 27 6. 22 and 26 Directions: Find each angle measure. 7. Given: wvm25-149 m21- 8. Given: mn: m1=74 mz2- m22- m.23- m23- mz4= V mz4= m25= m26- m26= m27- m27 m28- m48= 9. Given: a || b: m28 125 m2- 10. Given: xy: m22-22 m21- = mz2- m43- m3- mZA m24-> m. 5- m25- m26- m.26=> m2]=> m27= m28- 11. Given: rm2-29: m15-65 m2=> m29-> m3- m. 10- mc4= m25= m212- m.46- m213- mat- m214- m28- & Gina when (N) Things ALICE 2017arrow_forwardMatch each statement to the set of shapes that best describes them. 1. Similar triangles by SSS 2. Similar triangles by SAS 3. Similar triangles by AA 4. The triangles are not similar > U E 35° 89° S F 89° J 35° 94° G 52° 90° E K 52° Iarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY