Chapter 5.1, Problem 9E

Interpretation Introduction

Interpretation:

To sketch the vector field $\dot{\text{x}}\text{ = -y}$, $\dot{\text{y}}\text{ = -x}$. To show that the trajectories of the system are hyperbolas of the form ${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$. The equations for the stable and unstable manifolds of the origin is to be found. To rewrite the system in terms of new variables $\text{u}$ and $\text{v}$, and to solve for $\text{u(t)}$ and $\text{v(t)}$, starting from an arbitrary initial condition $\left({\text{u}}_{\text{0}}{\text{, v}}_{\text{0}}\right)$. The equations for the stable and unstable manifolds in terms of $\text{u}$ and $\text{v}$ is to be found. To write the general solution for $\text{x(t)}$ and $\text{y(t)}$, starting from an initial condition $\left({\text{x}}_{\text{0}}{\text{, y}}_{\text{0}}\right)$.

Concept Introduction:

The system assigns a vector $\left(\dot{\text{x}}\text{, }\dot{\text{y}}\right)$ at each point $\left(\text{x, y}\right)$, and represents a vector field on the phase plane.

Substitute the given system in the equation $\text{x}\dot{\text{x}}\text{ - y}\dot{\text{y}}\text{ = 0}$ to show that the trajectories of the system are hyperbolas of the form ${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$

The stable manifold of a fixed point is the set of all points in the plane which tends to the fixed point as time goes to positiveinfinity.

The unstable manifold for a fixed point is the set of all points in the plane which tends to the fixed point as time goes to negative infinity.

Answer to Problem 9E

Solution:

a) The vector field of the system $\dot{\text{x}}\text{ = -y}$, $\dot{\text{y}}\text{ = -x}$ is sketched

b) It is shown that the trajectories of the system are hyperbolas of the form ${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$

c) The equations for the stable and unstable manifolds for origin are $\text{y = x}$ and $\text{y = -x}$ respectively.

d) The solutions in terms of new variables $\text{u}$ and $\text{v}$, for the initial condition ${\text{(u}}_{\text{0}}{\text{, v}}_{\text{0}}\text{)}$ are ${\text{u(t) = u}}_{\text{0}}{\text{ e}}^{\text{- t}}$ and ${\text{v(t) = v}}_{\text{0}}{\text{ e}}^{\text{t}}$.

e) The equations for the stable and unstable manifolds in terms of $\text{u}$ and $\text{v}$ are $\text{v = 0}$ and $\text{u = 0}$ respectively.

f) The general solution for $\text{x(t)}$ and $\text{y(t)}$ is $\text{x(t) = }\frac{{\text{(x}}_{\text{0}}{\text{ + y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ + (x}}_{\text{0}}{\text{ - y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$ and $\text{y(t) = }\frac{{\text{(x}}_{\text{0}}{\text{ + y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ - (x}}_{\text{0}}{\text{ - y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$ respectively.

Explanation of Solution

a) The vector field of the given system $\dot{\text{x}}\text{ = -y}$, $\dot{\text{y}}\text{ = -x}$ is shown below

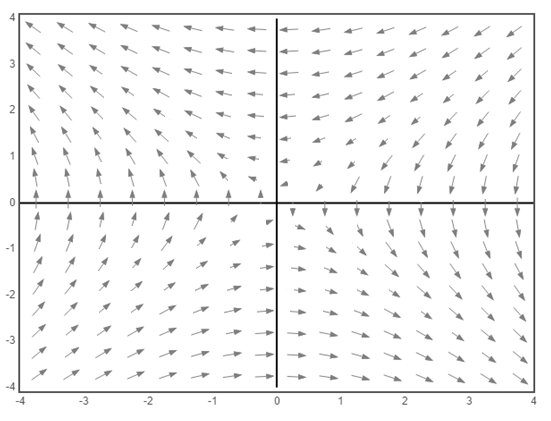
b) Consider the given system,

$\dot{\text{x}}\text{ = -y}$, $\dot{\text{y}}\text{ = -x}$.

It can be shown that the trajectories of the system are hyperbolas of the form ${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$ by using the equation,

$\text{x}\dot{\text{x}}\text{ - y}\dot{\text{y}}\text{ = 0}$

Substituting $\text{-y}$ for $\dot{\text{x}}$, and $\text{-x}$ for $\dot{\text{y}}$

$\text{(x)(-y) - (y)(-x) = 0}$

$\text{-xy + xy = 0}$

Thus, the given system implies $\text{x}\dot{\text{x}}\text{ - y}\dot{\text{y}}\text{ = 0}$

Integrating the above equation,

${\displaystyle \int \left(\text{x}\dot{\text{x}}\text{ - y}\dot{\text{y}}\right)}\text{dt = }{\displaystyle \int \text{0 dt}}$

${\text{x}}^{\text{2}}\text{- }{\displaystyle \int {\text{xdx = y}}^{\text{2}}\text{- }{\displaystyle \int \text{ydy}}}$

${\text{x}}^{\text{2}}\text{ - }\frac{{\text{x}}^{\text{2}}}{\text{2}}{\text{ = y}}^{\text{2}}\text{ - }\frac{{\text{y}}^{\text{2}}}{\text{2}}\text{ + C}$

${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$

Thus, the trajectory of the given system is the hyperbola of the form ${\text{x}}^{\text{2}}{\text{ - y}}^{\text{2}}\text{ = C}$.

c) The origin is a saddle point for the given system. From the sketch of the vector field, it is clear that the equation $\text{y = x}$ has vectors going towards the center or the fixed point, and is decaying. This means that the equation $\text{y = x}$ is the stable manifold.

Also, the equation $\text{y = -x}$ has vectors going away from the center or the fixed point, and is growing. This means the equation $\text{y = -x}$ is the unstable manifold.

This can also be proved by substituting $\text{x}$ for $\text{y}$ and $\text{y}$ for $\text{x}$ in the given equations,

$\dot{\text{x}}\text{ = -x}$ and $\dot{\text{y}}\text{ = -y}$

This linear system gives a stable fixed point.

Similarly, substituting $\text{-x}$ for $\text{y}$ and $\text{-y}$ for $\text{x}$ in the given equations,

$\dot{\text{x}}\text{ = x}$ and $\dot{\text{y}}\text{ = y}$

This linear system gives an unstable fixed point.

Therefore, the equations for the stable and unstable manifolds for origin is $\text{y = x}$ and $\text{y = -x}$ respectively.

d) Introducing new variables $\text{u}$ and $\text{v}$ such that

$\text{u = x + y}$ and $\text{v = x - y}$

The system can be rewritten as

$\dot{\text{u}}\text{ = }\dot{\text{x}}\text{ + }\dot{\text{y}}$ and $\dot{\text{v}}\text{ = }\dot{\text{x}}\text{ - }\dot{\text{y}}$

Substituting $\text{-y}$ for $\dot{\text{x}}$ and $\text{-x}$ for $\dot{\text{y}}$ in $\dot{\text{u}}\text{ = }\dot{\text{x}}\text{ + }\dot{\text{y}}$,

$\begin{array}{l}\dot{\text{u}}\text{ = -y - x}\\ \dot{\text{u}}\text{ = -(x + y)}\end{array}$

Again, substituting $\text{u}$ for $\text{(x + y)}$,

$\dot{\text{u}}\text{ = - u}$

The above equation can be also represented as

${\text{u(t) = ce}}^{\text{- t}}$

Solving for the initial conditions,

Substituting $\text{t = 0}$ in ${\text{u(t) = ce}}^{\text{-t}}$

$\begin{array}{l}{\text{u}}_{\text{0}}{\text{ = ce}}^{\text{0}}\\ {\text{u}}_{\text{0}}\text{ = c}\end{array}$

Substituting the value of $\text{c}$ back in the equation ${\text{u(t) = ce}}^{\text{-t}}$,

${\text{u(t) = u}}_{\text{0}}{\text{ e}}^{\text{- t}}$

Similarly substituting $\text{-y}$ for $\dot{\text{x}}$ and $\text{-x}$ for $\dot{\text{y}}$ in $\dot{\text{v}}\text{ = }\dot{\text{x}}\text{ - }\dot{\text{y}}$,

$\begin{array}{l}\dot{\text{v}}\text{ = -y + x}\\ \dot{\text{v}}\text{ = x - y}\end{array}$

Again, substituting $\text{v}$ for $\text{(x - y)}$

$\dot{\text{v}}\text{ = v}$

The above equation can be also represented as

${\text{v(t) = ce}}^{\text{t}}$

Solving for the initial conditions,

Substituting $\text{t = 0}$ in ${\text{v(t) = ce}}^{\text{t}}$,

$\begin{array}{l}{\text{v}}_{\text{0}}{\text{ = ce}}^{\text{0}}\\ {\text{v}}_{\text{0}}\text{ = c}\end{array}$

Substituting the value of $\text{c}$ back in the equation ${\text{v(t) = ce}}^{\text{t}}$,

${\text{v(t) = v}}_{\text{0}}{\text{ e}}^{\text{t}}$

Hence, the solutions of the linear equation for the initial condition ${\text{(u}}_{\text{0}}{\text{, v}}_{\text{0}}\text{)}$ is ${\text{u(t) = u}}_{\text{0}}{\text{ e}}^{\text{- t}}$ and ${\text{v(t) = v}}_{\text{0}}{\text{ e}}^{\text{t}}$.

e) Since the equations of the stable and unstable manifold are $\text{y = x}$ and $\text{y = -x}$ respectively.

Therefore, substituting $\text{y}$ for $\text{x}$ in the equation $\text{v = x - y}$,

$\begin{array}{l}\text{v = y - y}\\ \text{v = 0}\end{array}$

Similarly, substituting $\text{-y}$ for $\text{x}$ in $\text{u = x + y}$,

$\begin{array}{l}\text{u = -y + y}\\ \text{u = 0}\end{array}$

Thus, $\text{v = 0}$ and $\text{u = 0}$ are stable and unstable manifolds respectively in terms of $\text{u}$ and $\text{v}$

f) Since $\text{u = x + y}$ and $\text{v = x - y}$.

Solving the above equations to get the values of $\text{x}$ and $\text{y}$ in terms of $\text{u}$ and $\text{v}$,

$\text{x = }\frac{\text{u + v}}{\text{2}}$ and $\text{y = }\frac{\text{u - v}}{\text{2}}$

Substituting ${\text{u(t) = u}}_{\text{0}}{\text{ e}}^{\text{-t}}$ and ${\text{v(t) = v}}_{\text{0}}{\text{ e}}^{\text{t}}$ in $\text{x = }\frac{\text{u + v}}{\text{2}}$,

$\text{x = }\frac{{\text{u}}_{\text{0}}{\text{e}}^{\text{- t}}{\text{ + v}}_{\text{0}}{\text{e}}^{\text{t}}}{\text{2}}$

Again, substituting ${\text{(x}}_{\text{0}}{\text{+ y}}_{\text{0}}\text{)}$ for ${\text{u}}_{\text{0}}$ and ${\text{(x}}_{\text{0}}{\text{ - y}}_{\text{0}}\text{)}$ for ${\text{v}}_{\text{0}}$

$\text{x = }\frac{{\text{(x}}_{\text{0}}{\text{+ y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ + (x}}_{\text{0}}{\text{- y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$

Similarly, substituting ${\text{u}}_{\text{0}}{\text{e}}^{\text{- t}}$ for $\text{u}$ and ${\text{v}}_{\text{0}}{\text{e}}^{\text{t}}$ for $\text{v}$ in $\text{y =}\frac{\text{u - v}}{\text{2}}$,

$\text{y = }\frac{{\text{u}}_{\text{0}}{\text{e}}^{\text{- t}}{\text{ - v}}_{\text{0}}{\text{e}}^{\text{t}}}{\text{2}}$

Again, substituting ${\text{(x}}_{\text{0}}{\text{+ y}}_{\text{0}}\text{)}$ for ${\text{u}}_{\text{0}}$ and ${\text{(x}}_{\text{0}}{\text{ - y}}_{\text{0}}\text{)}$ for ${\text{v}}_{\text{0}}$,

$\text{y = }\frac{{\text{(x}}_{\text{0}}{\text{+ y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ - (x}}_{\text{0}}{\text{- y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$

Therefore, the general solution for $\text{x(t)}$ and $\text{y(t)}$ is $\text{x(t) = }\frac{{\text{(x}}_{\text{0}}{\text{ + y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ + (x}}_{\text{0}}{\text{ - y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$ and $\text{y(t) = }\frac{{\text{(x}}_{\text{0}}{\text{ + y}}_{\text{0}}{\text{) e}}^{\text{- t}}{\text{ - (x}}_{\text{0}}{\text{ - y}}_{\text{0}}{\text{) e}}^{\text{t}}}{\text{2}}$ respectively.