
Concept explainers
Interpretation:
To sketch the
Concept Introduction:
The system assigns a vector
Substitute the given system in the equation
The stable manifold of a fixed point is the set of all points in the plane which tends to the fixed point as time goes to positiveinfinity.
The unstable manifold for a fixed point is the set of all points in the plane which tends to the fixed point as time goes to negative infinity.
Answer to Problem 9E
Solution:
a) The vector field of the system
b) It is shown that the trajectories of the system are hyperbolas of the form
c) The equations for the stable and unstable manifolds for origin are
d) The solutions in terms of new variables
e) The equations for the stable and unstable manifolds in terms of
f) The general solution for
Explanation of Solution
a) The vector field of the given system
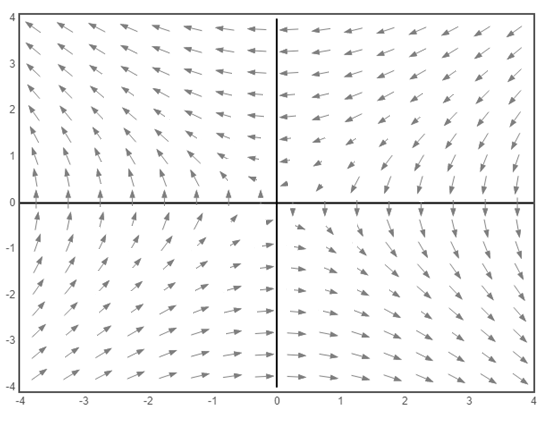
b) Consider the given system,
It can be shown that the trajectories of the system are hyperbolas of the form
Substituting
Thus, the given system implies
Integrating the above equation,
Thus, the trajectory of the given system is the hyperbola of the form
c) The origin is a saddle point for the given system. From the sketch of the vector field, it is clear that the equation
Also, the equation
This can also be proved by substituting
This linear system gives a stable fixed point.
Similarly, substituting
This linear system gives an unstable fixed point.
Therefore, the equations for the stable and unstable manifolds for origin is
d) Introducing new variables
The system can be rewritten as
Substituting
Again, substituting
The above equation can be also represented as
Solving for the initial conditions,
Substituting
Substituting the value of
Similarly substituting
Again, substituting
The above equation can be also represented as
Solving for the initial conditions,
Substituting
Substituting the value of
Hence, the solutions of the linear equation for the initial condition
e) Since the equations of the stable and unstable manifold are
Therefore, substituting
Similarly, substituting
Thus,
f) Since
Solving the above equations to get the values of
Substituting
Again, substituting
Similarly, substituting
Again, substituting
Therefore, the general solution for
Want to see more full solutions like this?
Chapter 5 Solutions
EBK NONLINEAR DYNAMICS AND CHAOS WITH S
- Q/ Find the Laurent series of (2-3) cos around z = 1 2-1arrow_forward31.5. Let be the circle |+1| = 2 traversed twice in the clockwise direction. Evaluate dz (22 + 2)²arrow_forwardUsing FDF, BDF, and CDF, find the first derivative; 1. The distance x of a runner from a fixed point is measured (in meters) at an interval of half a second. The data obtained is: t 0 x 0 0.5 3.65 1.0 1.5 2.0 6.80 9.90 12.15 Use CDF to approximate the runner's velocity at times t = 0.5s and t = 1.5s 2. Using FDF, BDF, and CDF, find the first derivative of f(x)=x Inx for an input of 2 assuming a step size of 1. Calculate using Analytical Solution and Absolute Relative Error: = True Value - Approximate Value| x100 True Value 3. Given the data below where f(x) sin (3x), estimate f(1.5) using Langrage Interpolation. x 1 1.3 1.6 1.9 2.2 f(x) 0.14 -0.69 -0.99 -0.55 0.31 4. The vertical distance covered by a rocket from t=8 to t=30 seconds is given by: 30 x = Loo (2000ln 140000 140000 - 2100 9.8t) dt Using the Trapezoidal Rule, n=2, find the distance covered. 5. Use Simpson's 1/3 and 3/8 Rule to approximate for sin x dx. Compare the results for n=4 and n=8arrow_forward
- 1. A Blue Whale's resting heart rate has period that happens to be approximately equal to 2π. A typical ECG of a whale's heartbeat over one period may be approximated by the function, f(x) = 0.005x4 2 0.005x³-0.364x² + 1.27x on the interval [0, 27]. Find an nth-order Fourier approximation to the Blue Whale's heartbeat, where n ≥ 3 is different from that used in any other posts on this topic, to generate a periodic function that can be used to model its heartbeat, and graph your result. Be sure to include your chosen value of n in your Subject Heading.arrow_forward7. The demand for a product, in dollars, is p = D(x) = 1000 -0.5 -0.0002x² 1 Find the consumer surplus when the sales level is 200. [Hints: Let pm be the market price when xm units of product are sold. Then the consumer surplus can be calculated by foam (D(x) — pm) dx]arrow_forward4. Find the general solution and the definite solution for the following differential equations: (a) +10y=15, y(0) = 0; (b) 2 + 4y = 6, y(0) =arrow_forward
- 5. Find the solution to each of the following by using an appropriate formula developed in the lecture slides: (a) + 3y = 2, y(0) = 4; (b) dy - 7y = 7, y(0) = 7; (c) 3d+6y= 5, y(0) = 0arrow_forward1. Evaluate the following improper integrals: (a) fe-rt dt; (b) fert dt; (c) fi da dxarrow_forward8. Given the rate of net investment I(t) = 9t¹/2, find the level of capital formation in (i) 16 years and (ii) between the 4th and the 8th years.arrow_forward
- 9. If the marginal revenue function of a firm in the production of output is MR = 40 - 10q² where q is the level of output, and total revenue is 120 at 3 units of output, find the total revenue function. [Hints: TR = √ MRdq]arrow_forward6. Solve the following first-order linear differential equations; if an initial condition is given, definitize the arbitrary constant: (a) 2 + 12y + 2et = 0, y(0) = /; (b) dy+y=tarrow_forward4. Let A = {a, b, c, d, e, f}, B = {e, f, g, h} and C = {a, e, h,i}. Let U = {a, b, c, d, e, f, g, h, i, j, k}. • Draw a Venn Diagram to describe the relationships between these sets Find (AB) NC • Find (AC) UB Find AUBUC • Find (BC) N (A - C)arrow_forward
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

