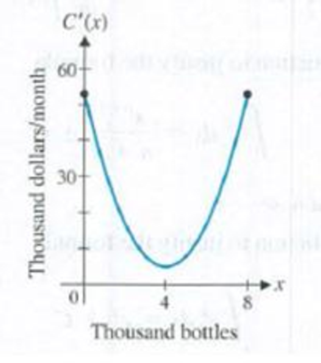
Problem 1MP: Matched Problem 1 Note that ddx(x3)=3x2 A. Find all antiderivatives of f(x) = 3x2. B. Graph the... Problem 2MP: Find each indefinite integral: (A) 2dx (B) 16etdt (C) 3x4dx (D) (2x53x2+1)dx (E) (5x4ex)dx Problem 3MP: Matched Problem 3 Find each indefinite integral: (A) (2x2/33x4)dx (B) 4w35dw (C) x48x3x2dx (D)... Problem 4MP: Matched Problem 4 Find the equation of the curve that passes through (2, 6) if the slope of the... Problem 5MP: Matched Problem 5 Find the revenue function R(x) when the marginal revenue is R(x)=4000.4x and no... Problem 6MP: Matched Problem 6 There are currently 64,000 subscribers to an online fashion magazine. Due to... Problem 1ED: Explore and Discuss 1 Formulas 1, 2, and 3 do not provide a formula for the indefinite integral of... Problem 1E: In Problems 18, write each function as a sum of terms of the form axn where a is a constant. (If... Problem 2E: In Problems 18, write each function as a sum of terms of the form axn where a is a constant. (If... Problem 3E: In Problems 18, write each function as a sum of terms of the form axn, where a is a constant. (If... Problem 4E: In Problems 18, write each function as a sum of terms of the form axn where a is a constant. (If... Problem 5E: In Problems 18, write each function as a sum of terms of the form axn where a is a constant. (If... Problem 6E Problem 7E: In Problems 18, write each function as a sum of terms of the form axn where a is a constant. (If... Problem 8E Problem 9E: In Problems 924, find each indefinite integral. Check by differentiating. 9. 7dx Problem 10E: In Problems 924, find each indefinite integral. Check by differentiating. 10. 10dx Problem 11E: In Problems 924, find each indefinite integral. Check by differentiating. 11. 8xdx Problem 12E: In Problems 924, find each indefinite integral. Check by differentiating. 12. 14xdx Problem 13E: In Problems 924, find each indefinite integral. Check by differentiating. 13. 9x2dx Problem 14E: In Problems 924, find each indefinite integral. Check by differentiating. 14. 15x2dx Problem 15E: In Problems 924, find each indefinite integral. Check by differentiating. 15. x5dx Problem 16E: In Problems 924, find each indefinite integral. Check by differentiating. 16. x8dx Problem 17E: In Problems 924, find each indefinite integral. Check by differentiating. 17. x3dx Problem 18E: In Problems 924, find each indefinite integral. Check by differentiating. 18. x4dx Problem 19E: In Problems 924, find each indefinite integral. Check by differentiating. 19. 10x3/2dx Problem 20E: In Problems 924, find each indefinite integral. Check by differentiating. 20. 8x1/3dx Problem 21E: In Problems 924, find each indefinite integral. Check by differentiating. 21. 3zdz Problem 22E: In Problems 924, find each indefinite integral. Check by differentiating. 22. 7zdz Problem 23E: In Problems 924, find each indefinite integral. Check by differentiating. 23. 16eudu Problem 24E: In Problems 924, find each indefinite integral. Check by differentiating. 24. 5eudu Problem 25E: Is F(x) = (x + 1) (x + 2) an antiderivative of f(x) = 2x + 3? Explain. Problem 26E Problem 27E: Is F(x) = 1 + x ln x an antiderivative of f(x) = 1 + ln x? Explain. Problem 28E: Is F(x) = x ln x x + e an antiderivative of f(x) = ln x? Explain. Problem 29E: Is F(x)=(2x+1)33 an antiderivative of f(x) = (2x + 1)2? Explain. Problem 30E: Is F(x)=(3x2)44 an antiderivative of f(x) = (3x 2)3? Explain. Problem 31E: Is F(x)=ex33an antiderivative of f(x)=ex2? Explain. Problem 32E: Is F(x) = (ex 10) (ex + 10) an antiderivative of f(x) = 2e2x? Explain. Problem 33E: In Problems 3338, discuss the validity of each statement. If the statement is always true, explain... Problem 34E: In Problems 3338, discuss the validity of each statement. If the statement is always true, explain... Problem 35E: In Problems 3338, discuss the validity of each statement. If the statement is always true, explain... Problem 36E Problem 37E: In Problems 3338, discuss the validity of each statement. If the statement is always true, explain... Problem 38E: In Problems 3338, discuss the validity of each statement. If the statement is always true, explain... Problem 39E: In Problems 3942, could the three graphs in each figure be anti-derivatives of the same function?... Problem 40E: In Problems 3942, could the three graphs in each figure be anti-derivatives of the same function?... Problem 41E: In Problems 39-42, could the three graphs in each figure be anti-derivatives of the same function?... Problem 42E: In Problems 39-42, could the three graphs in each figure be anti-derivatives of the same function?... Problem 43E: In Problems 4354, find each indefinite integral (Check by differentiation.) 43. 5x(1x)dx Problem 44E: In Problems 4354, find each indefinite integral (Check by differentiation.) 44. x2(1+x3)dx Problem 45E: In Problems 4354, find each indefinite integral (Check by differentiation.) 45. duu Problem 46E: In Problems 4354, find each indefinite integral (Check by differentiation.) 46. dtt3 Problem 47E: In Problems 4354, find each indefinite integral (Check by differentiation.) 47. dx4x3 Problem 48E: In Problems 4354, find each indefinite integral (Check by differentiation.) 48. 6dmm2 Problem 49E: In Problems 4354, find each indefinite integral (Check by differentiation.) 49. 4+uudu Problem 50E: In Problems 4354, find each indefinite integral (Check by differentiation.) 50. 1y23ydy Problem 51E: In Problems 4354, find each indefinite integral (Check by differentiation.) 51. (5ez+4)dz Problem 52E: In Problems 4354, find each indefinite integral (Check by differentiation.) 52. ett2dt Problem 53E: In Problems 4354, find each indefinite integral (Check by differentiation.) 53. (3x22x2) Problem 54E: In Problems 4354, find each indefinite integral (Check by differentiation.) 54. (4x3+2x3)dx Problem 55E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 56E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 57E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 58E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 59E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 60E: In Problems 5562, find the particular antiderivative of each derivative that satisfies the given... Problem 61E: In Problems 55-62, find the particular antiderivative of each derivative that satisfies the given... Problem 62E: In Problems 55-62, find the particular antiderivative of each derivative that satisfies the given... Problem 63E: Find the equation of the curve that passes through (2,3) if its slope is given by dydx=4x3 for each... Problem 64E: Find the equation of the curve that passes through (1,3) if its slope is given by dydx=12x212x For... Problem 65E: In Problems 65-70, find each indefinite integral. 65. 2x4xx3dx Problem 66E: In Problems 6570, find each indefinite integral. 66. x1x4x2dx Problem 67E: In Problems 6570, find each indefinite integral. 67. x52xx4dx Problem 68E: In Problems 6570, find each indefinite integral. 68. 13x4x2dx Problem 69E: In Problems 6570, find each indefinite integral. 69. x2ex2xx2dx Problem 70E: In Problems 6570, find each indefinite integral. 70. 1xexxdx Problem 71E: In Problems 7174, find the derivative or indefinite integral as indicated. 71. ddx(6x27x+2)dx Problem 72E: In Problems 7174, find the derivative or indefinite integral as indicated. 72. ddx(4x23x+5)dx Problem 73E: In Problems 7174, find the derivative or indefinite integral as indicated. 73. ddtt2lnt3t+2dt Problem 74E Problem 75E: In Problems 7174, find the derivative or indefinite integral as indicated. xndx=xn+1n+1+C provided... Problem 76E: Use differentiation to justify the formula exdx=ex+C Problem 77E: Assuming that x 0, use differentiation to justify the formula 1xdx=lnx+C Problem 78E: Assuming that x 0, use differentiation to justify the formula 1xdx=lnx+C [Hint: Use the chain rule... Problem 79E: Show that the indefinite integral of the sum of two functions is the sum of the indefinite... Problem 80E Problem 81E: Cost function. The marginal average cost of producing x smart watches is given by... Problem 82E: Renewable energy. In 2016, U.S. consumption of renewable energy was 9.97 quadrillion Btu (or 9.97 ... Problem 83E: Production costs. The graph of the marginal cost function from the production of x thousand bottles... Problem 84E: Revenue. The graph of the marginal revenue function from the sale of x smart watches is given in the... Problem 85E: Soles analysis. Monthly sales of an SUV model are expected to increase at the rate of S(t)=24t1/3... Problem 86E: Sales analysis. The rate of change of the monthly sales of a newly released football game is given... Problem 87E: Soles analysis. Repeat Problem 85 if S(t)=24t1/370 and all other information remains the same. Use a... Problem 88E: 88. Sales analysis. Repeat Problem 86 if S'(t) = 500t1/4 + 300 and all other information remains the... Problem 89E: Labor costs. A defense contractor is starting production on a new missile control system. On the... Problem 90E: Labor costs. If the rate of labor use in Problem 89 is L(x)=2,000x1/3 and if the first 8 control... Problem 91E: Weightheight. For an average person, the rate of change of weight W (in pounds) with respect to... Problem 92E Problem 93E: Urban growth. The rate of growth of the population N(t) of a new city t years after its... Problem 94E: Learning. A college language class was chosen for an experiment in learning. Using a list of 50... format_list_bulleted


 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning



