MYLAB W/ETEXT FOR MATHEMATICS ALL AROUN
MYLAB W/ETEXT FOR MATHEMATICS ALL AROUN
6th Edition
ISBN: 9780135902783
Author: Pirnot
Publisher: PEARSON
bartleby

Concept explainers

Counting Principles
In statistics, the counting principle can be said to be the concept in which the quantity of an item is determined. There can be a single item, or a group of items, or items that are related to each other. In every possible set of items, the quantity of …
bartleby

Videos

Textbook Question
Book Icon
Chapter 5.1, Problem 79E

Egyptian mathematics had a unique way of writing fractions as sums of unit fractions – that is, fractions of the form 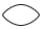  1 n . For example, the fraction 2 9 could be written as 1 6 + 1 18 and also as 1 5 + 1 45 . They would not represent a number like 2 3 as   1 3 + 1 3 ; they would use two different unit fractions. Unit fractions were written by placing the symbol Chapter 5.1, Problem 79E, Egyptian mathematics had a unique way of writing fractions as sums of unit fractions that is, , example 1, which looked somewhat like an eye, over the numeral. For example, 1 3 could be written asChapter 5.1, Problem 79E, Egyptian mathematics had a unique way of writing fractions as sums of unit fractions that is, , example 2. In exercises   79   −   82 , write the given fractions as the sum of unit fractions, using our common notation rather than the cumbersome Egyptian notation. (There may be several correct answers but we will give only one.)

2 3

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 5.1, Problem 78E
Next
Chapter 5.1, Problem 80E
Students have asked these similar questions
3. Let sin (22) + cos (T2) f(z) = z(22 + 1)(z+1) Compute f(z)dz over each of the contours/closed curves C1, C2, C3 and C4 shown below. L 10 -C x Don't use any Al tool show ur answer pe n and paper then take
what is the slope of the linear equation-5x+2y-10=0
1. Evaluate (2,5) (3x+y)dx+(2y-x)dy (0,1) (i) along the straight lines from (0, 1) to (2, 1) and then from (2, 1) to (2,5), and (ii) along the parabola y = x² + 1. Don't use any Al tool show ur answer in pe n and paper then take

Chapter 5 Solutions

MYLAB W/ETEXT FOR MATHEMATICS ALL AROUN

Ch. 5.1 - Write the Egyptian numerals using Hindu-Arabic...Ch. 5.1 - Write the Egyptian numerals using Hindu-Arabic...Ch. 5.1 - Prob. 3ECh. 5.1 - Write the Egyptian numerals using Hindu-Arabic...Ch. 5.1 - Write each Hindu-Arabic numeral using Egyptian...Ch. 5.1 - Write each Hindu-Arabic numeral using Egyptian...Ch. 5.1 - Prob. 7ECh. 5.1 - Write each Hindu-Arabic numeral using Egyptian...Ch. 5.1 - Prob. 9ECh. 5.1 - Perform each of the following addition problems...
Ch. 5.1 - Prob. 11ECh. 5.1 - Perform each of the following addition problems...Ch. 5.1 - Perform each of the following subtraction problems...Ch. 5.1 - Perform each of the following subtraction problems...Ch. 5.1 - Perform each of the following subtraction problems...Ch. 5.1 - Perform each of the following subtraction problems...Ch. 5.1 - Prob. 17ECh. 5.1 - Use the Egyptian method of doubling to calculate...Ch. 5.1 - Prob. 19ECh. 5.1 - Use the Egyptian method of doubling to calculate...Ch. 5.1 - Prob. 21ECh. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Write each Roman numeral using Hindu-Arabic...Ch. 5.1 - Prob. 31ECh. 5.1 - Write each numeral in Roman notation There may be...Ch. 5.1 - Prob. 33ECh. 5.1 - Write each numeral in Roman notation There may be...Ch. 5.1 - Prob. 35ECh. 5.1 - Write each numeral in Roman notation There may be...Ch. 5.1 - Prob. 37ECh. 5.1 - Write each numeral in Roman notation There may be...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each Chinese numeral as a Hindu-Arabic...Ch. 5.1 - Write each numeral using Chinese numerals. 495Ch. 5.1 - Write each numeral using Chinese numerals. 726Ch. 5.1 - Write each numeral using Chinese numerals. 2,805Ch. 5.1 - Write each numeral using Chinese numerals. 3,926Ch. 5.1 - Write each numeral using Chinese numerals. 9,846Ch. 5.1 - Write each numeral using Chinese numerals. 8,054Ch. 5.1 - The Great Pyramid at Giza was completed in . Write...Ch. 5.1 - Cheops, the builder of the Great Pyramid at Giza,...Ch. 5.1 - An Egyptian merchant has a warehouse that contains...Ch. 5.1 - An ancient Egyptian merchant had on hand bushels...Ch. 5.1 - Using Egyptian notation, the number 100,...Ch. 5.1 - Using Egyptian notation, the number 100,...Ch. 5.1 - Using Egyptian notation, the number 100,...Ch. 5.1 - Using Egyptian notation, the number 100,...Ch. 5.1 - The emperor Aurelius Constantine, who lived from...Ch. 5.1 - By 285ad, the Roman Empire had become so vast that...Ch. 5.1 - Frequently, Roman numerals are used today in movie...Ch. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Frequently, Roman numerals are used today in movie...Ch. 5.1 - The counting boards In Exercises 6568 show...Ch. 5.1 - The counting boards In Exercises 6568 show...Ch. 5.1 - The counting boards In Exercises 6568 show...Ch. 5.1 - The counting boards In Exercises 6568 show...Ch. 5.1 - The oldest discovery of Chinese written numerals...Ch. 5.1 - When Marco Polo visited China in 1274, he was...Ch. 5.1 - Explain two advantages of the Roman numeration...Ch. 5.1 - The Roman numeration system has symbols for 5,50,...Ch. 5.1 - The traditional Chinese numeration system had no...Ch. 5.1 - Research the Ionic Greek numeration system, which...Ch. 5.1 - In the Egyptian numeration system, whenever we...Ch. 5.1 - Suppose that Egyptian numeration was based on 5...Ch. 5.1 - Invent an Egyptian type of numeration system using...Ch. 5.1 - Write the number 1,999 in Roman numerals in as...Ch. 5.1 - Egyptian mathematics had a unique way of writing...Ch. 5.1 - Egyptian mathematics had a unique way of writing...Ch. 5.1 - Egyptian mathematics had a unique way of writing...Ch. 5.1 - Egyptian mathematics had a unique way of writing...Ch. 5.2 - Write the following Babylonian numerals as...Ch. 5.2 - Write the following Babylonian numerals as...Ch. 5.2 - Write the following Babylonian numerals as...Ch. 5.2 - Write the following Babylonian numerals as...Ch. 5.2 - Write each number using Babylonian notation. 8,235Ch. 5.2 - Write each number using Babylonian notation. 7,331Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Write each number using Babylonian notation....Ch. 5.2 - Translate each of the following Mayan numerals to...Ch. 5.2 - Translate each of the following Mayan numerals to...Ch. 5.2 - Translate each of the following Mayan numerals to...Ch. 5.2 - Translate each of the following Mayan numerals to...Ch. 5.2 - Write each number using Mayan notation. 17Ch. 5.2 - Write each number using Mayan notation. 48Ch. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - Prob. 75ECh. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Prob. 78ECh. 5.2 - Prob. 79ECh. 5.2 - Prob. 80ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - Prob. 73ECh. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - Prob. 77ECh. 5.3 - Prob. 78ECh. 5.3 - Prob. 79ECh. 5.3 - Prob. 80ECh. 5.3 - Prob. 81ECh. 5.3 - Prob. 82ECh. 5.3 - Prob. 83ECh. 5.3 - Prob. 84ECh. 5.3 - Prob. 85ECh. 5.3 - Prob. 86ECh. 5.3 - Prob. 87ECh. 5.3 - Prob. 88ECh. 5.3 - Prob. 89ECh. 5.3 - Prob. 90ECh. 5.3 - Prob. 91ECh. 5.3 - Prob. 92ECh. 5.3 - Prob. 93ECh. 5.3 - Prob. 94ECh. 5.3 - Prob. 95ECh. 5.3 - Prob. 96ECh. 5.3 - Prob. 97ECh. 5.3 - Prob. 98ECh. 5.3 - Prob. 99ECh. 5.3 - Prob. 100ECh. 5.3 - Prob. 101ECh. 5.3 - Prob. 102ECh. 5.4 - Prob. 1ECh. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - a. Why are check digits important? Give an...Ch. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - Prob. 62ECh. 5.4 - Prob. 63ECh. 5.4 - Challenge Yourself When we do usual division of...Ch. 5.4 - Prob. 65ECh. 5.CR - Prob. 1CRCh. 5.CR - Prob. 2CRCh. 5.CR - Prob. 3CRCh. 5.CR - Prob. 4CRCh. 5.CR - Prob. 5CRCh. 5.CR - Prob. 6CRCh. 5.CR - Prob. 7CRCh. 5.CR - Prob. 8CRCh. 5.CR - Prob. 9CRCh. 5.CR - Prob. 10CRCh. 5.CR - Prob. 11CRCh. 5.CR - Prob. 12CRCh. 5.CR - Prob. 13CRCh. 5.CR - Prob. 14CRCh. 5.CR - Prob. 15CRCh. 5.CR - Prob. 16CRCh. 5.CR - Prob. 17CRCh. 5.CR - Prob. 18CRCh. 5.CR - Prob. 19CRCh. 5.CR - Prob. 20CRCh. 5.CR - Prob. 21CRCh. 5.CR - Prob. 22CRCh. 5.CR - Prob. 23CRCh. 5.CT - Write 3,685 in Roman notation.Ch. 5.CT - Prob. 2CTCh. 5.CT - Write 2647 and A3E16 as base-10 numerals.Ch. 5.CT - Prob. 4CTCh. 5.CT - Prob. 5CTCh. 5.CT - Prob. 6CTCh. 5.CT - Prob. 7CTCh. 5.CT - Prob. 8CTCh. 5.CT - Prob. 9CTCh. 5.CT - Prob. 10CTCh. 5.CT - Prob. 11CTCh. 5.CT - Prob. 12CTCh. 5.CT - Prob. 13CTCh. 5.CT - Prob. 14CTCh. 5.CT - Prob. 15CTCh. 5.CT - Prob. 16CTCh. 5.CT - Prob. 17CTCh. 5.CT - Prob. 18CTCh. 5.CT - Prob. 19CTCh. 5.CT - Prob. 20CTCh. 5.CT - Prob. 21CTCh. 5.CT - Prob. 22CT
Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
SEE MORE TEXTBOOKS
The Fundamental Counting Principle; Author: AlRichards314;https://www.youtube.com/watch?v=549eLWIu0Xk;License: Standard YouTube License, CC-BY
The Counting Principle; Author: Mathispower4u;https://www.youtube.com/watch?v=qJ7AYDmHVRE;License: Standard YouTube License, CC-BY