Chapter 5.1, Problem 52PPSE

Solution

A

To Find : The effect of function on polynomial function and for each set B.

A linear function from A to B is always an onto function.

Where B equals all real numbers

Given information : The polynomial function is linear and set B are all real number.

Concept used : A function is called onto if it pairs every element in B with at least one element in A.

Calculation:

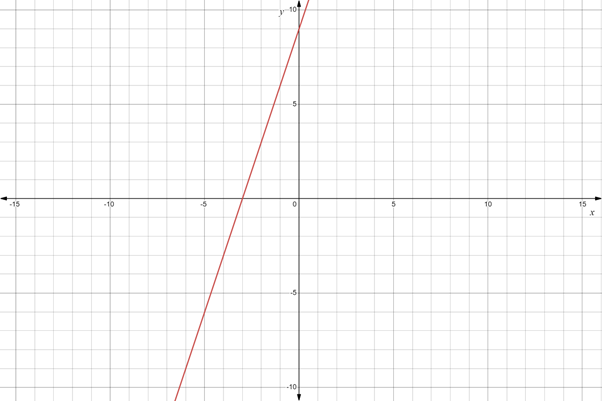
A linear polynomial function is of the form $p\left(x\right)=a_{1}x+a_0$

The End behavior is down and up, if $a_1$ is positive

The End behavior is up and down, if $a_1$ is negative

In both cases $p\left(x\right)$ will take all values between $-\infty$ and $+\infty$ , because polynomial functions are continuous.

Therefore, $p\left(x\right)$ will take all real values.

Hence a linear function is always an onto function from A to B where B is the set of all real numbers

Example: $y=3x+9$ , its graph is shown as

  

B

To determine : To determine the effect of function on polynomial function and for each set B.

A quadratic function from A to B is NEVER an ONTO function.

Where B equals all real numbers

Given information : The polynomial function is quadratic and set B are all real number.

Concept used : A function is called onto if it pairs every element in B with at least one element in A.

Calculation:

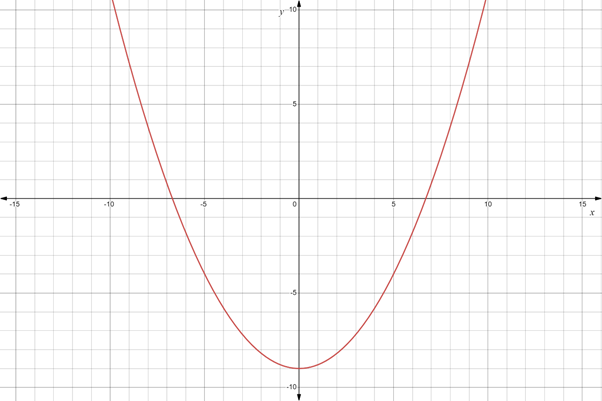
A quadratic polynomial function is of the form $p\left(x\right)=a_2{x}^2+a_1{x}_1+a_0$

The End behaviour is UP and UP , If $a_2$ is positive

The End behaviour is DOWN and DOWN , If $a_2$ is negative

A quadratic Function is a polynomial of even degree; therefore, it must have odd number of turning points.

Also, it is having degree 2, therefore, it can have at most $2-1=1$ number of turning points.

Therefore, a quadratic function will always have one turning point.

  $p\left(x\right)$ will have a maximum value if $a_2$ is negative, hence $p\left(x\right)$ will not take values greater than the maximum value.

  $p\left(x\right)$ will have a minimum value if $a_2$ is positive, hence $p\left(x\right)$ will not take values less than the minimum value.

In both cases $p\left(x\right)$ will not take all the real values.

Hence a quadratic function is NEVER an ONTO function from A to B where B= all real numbers

Example: $y=\frac{x^2}{5}-9$ , its graph is shown as

  

C

To determine : The effect of function on polynomial function and for each set B.

A quadratic function from A to B is SOMETIMES an ONTO function.

Where B equals all real numbers greater than or equal to 4.

Given information : The polynomial function is quadratic and set B are all real number greater than or equal to 4.

Concept used : A function is called onto if it pairs every element in B with at least one element in A.

Calculation:

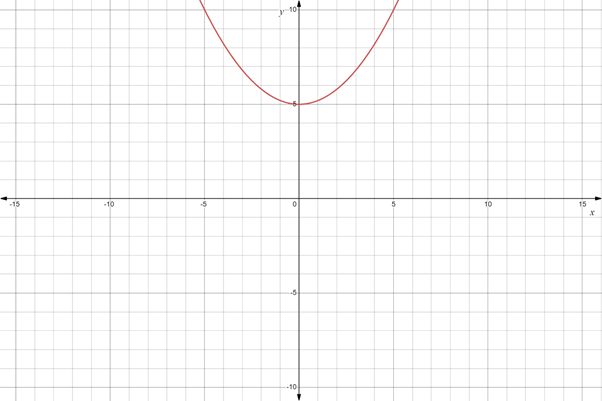
A quadratic polynomial function is of the form $p\left(x\right)=a_2{x}^2+a_1{x}_1+a_0$

The End behaviour is UP and UP , If $a_2$ is positive

The End behaviour is DOWN and DOWN , If $a_2$ is negative

A quadratic Function is a polynomial of even degree; therefore, it must have odd number of turning points.

Also, it is having degree 2, therefore, it can have at most $2-1=1$ number of turning points.

Therefore, a quadratic function will always have one turning point.

  $p\left(x\right)$ will have a maximum value if $a_2$ is negative, hence $p\left(x\right)$ will not take values greater than the maximum value.

Therefore, when $a_2$ is negative, $p\left(x\right)$ is NEVER an ONTO function from A to B where B= all real numbers greater than or equal to 4.

  $p\left(x\right)$ will have a minimum value if $a_2$ is positive, hence $p\left(x\right)$ will not take values less than the minimum value.

Therefore, when $a_2$ is positive, $p\left(x\right)$ is an ONTO function from A to B where B= all real numbers greater than or equal to 4.

Hence a quadratic function is SOMETIME an ONTO function from A to B where B= all real numbers greater than or equal to 4.

Example: $y=\frac{x^2}{5}+5$ , its graph is shown as

  

D

To determine : The effect of function on polynomial function and for each set B.

A cubic function from A to B is ALWAYS an ONTO function.

Where B equals all real numbers

Given information : The polynomial function is cubic and set B are all real number.

Concept used:

A function is called onto if it pairs every element in B with at least one element in A.

Calculation:

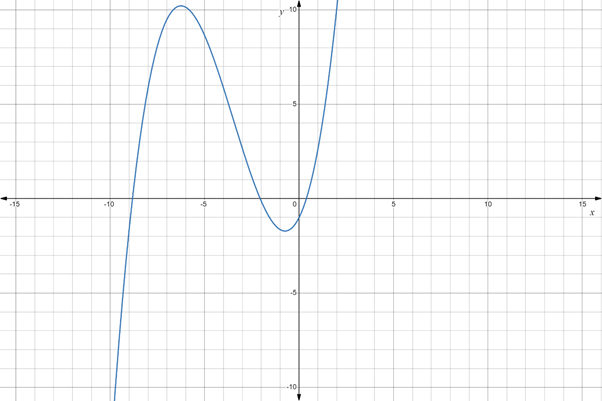
A cubic polynomial function is of the form $p\left(x\right)=a_3{x}^2+a_2{x}^2+a_{1}x+a_0$

The End behaviour is DOWN and UP , If $a_3$ is positive

The End behaviour is UP and DOWN , If $a_3$ is negative

In both cases $p\left(x\right)$ will take all values between $-\infty$ and $+\infty$ , because polynomial functions are continuous.

Therefore, $p\left(x\right)$ will take all real values.

Hence a cubic function is ALWAYS an ONTO function from A to B where B= all real numbers

Example: $y=\frac{x^3}{7}+\frac{3x^2}{2}+2x-1$ , its graph is shown as