Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 50, Problem 7A
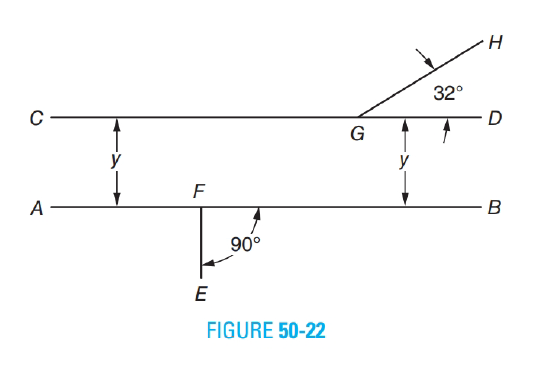
Refer to Figure 50-22 and identify each of the following as parallel, perpendicular, or oblique lines.
a. Line AB and line CD
b. Line AB and EF
c. Line CD and GH
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
If
AxB=xi-yj+zk
Then
B× A is
xi-yj+zk
-xi+yj-zkyj+zk
-yj+zk
No chatgpt pls will upvote
Not use ai please
Chapter 50 Solutions
Mathematics For Machine Technology
Ch. 50 - Refer to the Decimal-Inch Spur Gears Table under...Ch. 50 - If the cutting speed is 160 m/min and the...Ch. 50 - Solve the equation 28A2=(5+A)(2A)for A.Ch. 50 - Use the addition of equality to solve...Ch. 50 - If a=5.2,b=4.8,and c=7.25 ,what is the value of...Ch. 50 - Read the setting in Figure 50-21 of the metric...Ch. 50 - Refer to Figure 50-22 and identify each of the...Ch. 50 - Prob. 8ACh. 50 - Write the symbols for the following words. a....Ch. 50 - Express the following decimal degrees as degrees...
Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Determine 1.Ch. 50 - Determine 2.Ch. 50 - Determine 3.Ch. 50 - Determine 1+2+3.Ch. 50 - Determine 5.Ch. 50 - Determine 6.Ch. 50 - Determine 7+8+9Ch. 50 - Determine 1+2+3+4+5.Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - In the figure shown, 1=2=42. Determine 3.Ch. 50 - IF x=3914,find 4.Ch. 50 - In the figure shown, 1=2=3=4=5=5403. Determine 6.Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - The sum of the angles in figure equals shown...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Derive the projection matrix for projecting vectors onto a subspace defined by given basis vectors. • Verify that the projection matrix is idempotent and symmetric. • Compute the projection of a specific vector and check your result step-by-step. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardFind only the residues don't share the same pic as answer else I'll report Find the residue of F(z) = cot z coth z Don't use any Al tool show ur answer in pe n and paper then take z³ at z = 0.arrow_forward1. [10 points] Given y₁(x) = x²² is a solution to the differential equation x²y"+6xy'+6y=0 (x>0), find a second linearly independent solution using reduction of order.arrow_forward
- >tt 1:32 > trend.1m 1m (sales > summary(trend.1m) - tt) #3###23 (i) #### Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2107.220 57.997 36.332e-16 *** tt -43.500 3.067 -14.18 7.72e-15 *** > trend = ts (fitted (trend.1m), start-start (sales), freq-frequency (sales)) sales trend ###23%23 (ii) #### as.numeric((1:32 %% 4) > X > q1 > q2 > q3 > 94 = = = = - as.numeric((1:32 %% 4) as.numeric((1:32 %% 4) as.numeric((1:32 %% 4) == 1) 2) == == 3) == 0) > season.lm = 1m (resid (trend.1m) 0+q1 + q2 + q3 + q4) #3##23%23 (iii) #### > summary(season.1m) Coefficients: Estimate Std. Error t value Pr(>|t|) q1 -38.41 43.27 -0.888 0.38232 92 18.80 43.27 0.435 0.66719 q3 -134.78 43.27 -3.115 0.00422 ** 94 154.38 43.27 3.568 0.00132 ** > season = ts (fitted (season.lm), start=start (sales), freq=frequency (sales)) > Y X season %23%23%23%23 (iv) #### >ar (Y, aic=FALSE, order.max=1) #23%23%23%23 (v) #### Coefficients: 1 0.5704 Order selected 1 sigma 2 estimated as 9431 > ar(Y, aic=FALSE,…arrow_forwardRefer to page 52 for solving the heat equation using separation of variables. Instructions: • • • Write the heat equation in its standard form and apply boundary and initial conditions. Use the method of separation of variables to derive the solution. Clearly show the derivation of eigenfunctions and coefficients. Provide a detailed solution, step- by-step. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 20 for orthogonalizing a set of vectors using the Gram-Schmidt process. Instructions: • Apply the Gram-Schmidt procedure to the given set of vectors, showing all projections and subtractions step-by-step. • Normalize the resulting orthogonal vectors if required. • Verify orthogonality by computing dot products between the vectors. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forward
- Refer to page 54 for solving the wave equation. Instructions: • Apply d'Alembert's solution method or separation of variables as appropriate. • Clearly show the derivation of the general solution. • Incorporate initial and boundary conditions to obtain a specific solution. Justify all transformations and integrations. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 14 for calculating eigenvalues and eigenvectors of a matrix. Instructions: • Compute the characteristic polynomial by finding the determinant of A - XI. • Solve for eigenvalues and substitute them into (A - I) x = 0 to find the eigenvectors. • Normalize the eigenvectors if required and verify your results. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardExilet x = {a,b.c}dex.x―R> d(a,b) = d(b, c)=1' d(a, c) = 2 d(xx)=0VXEX is (x.d) m.s or not? 3.4 let x= d ((x,y), (3arrow_forward
- Hiw Show that sup (0,1) = 1 الفصل الثاني * Dif: let {an} be Seq. then fan?arrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. 1. The probability of a soccer game in a particular league going into overtime is 0.125. Find the following: a. The odds in favour of a game going into overtime. b. The odds in favour of a game not going into overtime. c. If the teams in the league play 100 games in a season, about how many games would you expect to go into overtime?arrow_forwardThe probability of being born in a particular month is about 1:12. Determine the probability of not being born in September. Express this ratio as a fraction, a decimal, a percent and in words.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning 
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY