Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 50, Problem 55A
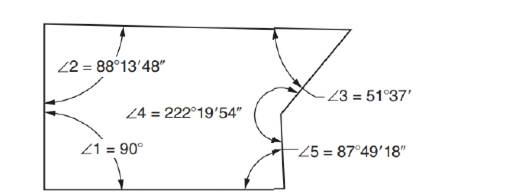
Determine
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
=
Use Qin's method to solve the pure cubic equation x³:
12,812,904. Compare this method with the old cube root
algorithm discussed in the text. In each case, show where
Collaborative Work (Ch4)
MA244-02_Collaborative_Work_Chapter4.pdf
uah.instructure.com
zm Rich LTI
b Answered: HW_#6 HW_06.pdf EE 213-01 Assignments zm Rich LTI uah.instruct...
✓ Download
→ Info
× Close
0
-
ZOOM +
1) a) Determine which functions are solutions of the following
linear differential equation:
y"- 6y' + 9y=0
i) e³x
isė
зх
23x
ii) xe ³x iii) x² ³x iv) (x+3) e³x
3×
хе
b) Find the Wronskion
хе
the set of functions that you fand
for
as the solution of the differential equation above
from a)
c) What does the result that you found from b) imply?
conici
2) Perform a rotation of axes to eliminate the xy-term,
identify and sketch the graph of the following a
5x²-2xy + Sy²=24=0
Use the Chinese cube root algorithm to find the cube root
of 12,812,904.
Chapter 50 Solutions
Mathematics For Machine Technology
Ch. 50 - Refer to the Decimal-Inch Spur Gears Table under...Ch. 50 - If the cutting speed is 160 m/min and the...Ch. 50 - Solve the equation 28A2=(5+A)(2A)for A.Ch. 50 - Use the addition of equality to solve...Ch. 50 - If a=5.2,b=4.8,and c=7.25 ,what is the value of...Ch. 50 - Read the setting in Figure 50-21 of the metric...Ch. 50 - Refer to Figure 50-22 and identify each of the...Ch. 50 - Prob. 8ACh. 50 - Write the symbols for the following words. a....Ch. 50 - Express the following decimal degrees as degrees...
Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the following decimal degrees as degrees...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the decimal degrees as degrees, minutes,...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees and minutes as...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Express the following degrees, minutes, and...Ch. 50 - Determine 1.Ch. 50 - Determine 2.Ch. 50 - Determine 3.Ch. 50 - Determine 1+2+3.Ch. 50 - Determine 5.Ch. 50 - Determine 6.Ch. 50 - Determine 7+8+9Ch. 50 - Determine 1+2+3+4+5.Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Subtract the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - Multiply the angles in each of the following...Ch. 50 - In the figure shown, 1=2=42. Determine 3.Ch. 50 - IF x=3914,find 4.Ch. 50 - In the figure shown, 1=2=3=4=5=5403. Determine 6.Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - Divide the angles in each of the following...Ch. 50 - The sum of the angles in figure equals shown...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Phil has systematically contributed $3000 to his RRSP at the beginning of every three months for the past 17 years.If the RRSP has earned 8.8% compounded quarterly, what is the value of Phil’s RRSP today? (Do not round intermediate calculations and round your final answer to 2 decimal places.)The value of the RRSP today $arrow_forwardAnswer this pleasearrow_forwardCan you prove that P(a,b) >= P(a',b) for a >= a' >= b >= 0arrow_forward
- Figure 1 Simulation structure diagram for a turbine cold-end system. approximated by the two fourth degree polynomial equations as follows: The turbine "cold-and" system generally consists of turbine exhaust and condenser, and cooling tower (Fig. 1). For a 250 MW unit, the turbine performance data with the maximum steam throttle flow can be NHR NEW NHR Turbine and NHR = −45.19(CP)* + 420(CP)® – 1442(CP)2 + 2248(CP) +6666 (a) NKW = 4,883(CP)* – 44,890(CP)3 + 152,600(CP)2 – 231,500(CP) + 383,400. (b) The condenser and mechanical-draft cooling tower have the performance equations, respectively, CP 1.6302-0.50095 x 10-1 (CWT) OP Coupling 1 Condenser CR WFR CWT Coupling 2 WST Cooling Tower CR System Boundary 2 (The circulating water flow is assumed to flow at the rate of 145,000 gpm.) In addition to the given performance equations give above, we also need two coupling equations to complete the mathematical model for this cooling system. The first equation is the coupling between the…arrow_forwardCan you evaluate the following for n >0?arrow_forwardDraw scale 1 unit=8 ftarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY