
Concept explainers
Refer to the
- i. P(S)
- ii. P(W)
- iii. P(S|W)
- iv. P(S|B)
- v. P(S and W)
- vi. P(N and B)
Smoking by Race for Males Aged 18–24
a.
Calculate each probability (i-vi) and explain it meaning in words.
Answer to Problem 94CE
i. The probability
ii. The probability
iii. The probability
iv. The probability
v. The probability
vi. The probability
Explanation of Solution
Calculation:
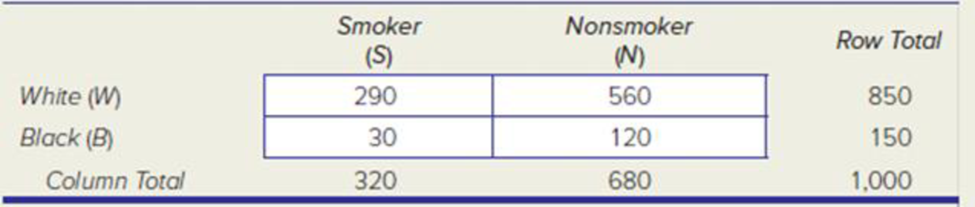
The given table shows that the smoking by race for males aged 18-24.
The given contingency table is,
| Smoker (S) | Nonsmoker (N) | Row Total | |
| White (W) | 290 | 560 | 850 |
| Black (B) | 30 | 120 | 150 |
| Column Total | 320 | 680 | 1,000 |
For (i)
The formula for finding the probability
Substitute 320 for ‘Frequency for the class S’ and 1,000 for ‘Total frequencies in the distribution’
Therefore, the probability
For (ii)
The formula for finding the probability
Substitute 850 for ‘Frequency for the class W’ and 1,000 for ‘Total frequencies in the distribution’
Therefore, the probability
For (iii)
The formula for finding the probability
Substitute 290 for ‘Frequency for the class S and W’ and 850 for ‘Frequency for the class W’,
Therefore, the probability
For (iv)
The formula for finding the probability
Substitute 30 for ‘Frequency for the class S and B’ and 150 for ‘Frequency for the class B’,
Therefore, the probability
For (v)
The formula for finding the probability
Substitute 290 for ‘Frequency for the class S and W’ and 1,000 for ‘Total frequencies in the distribution’,
Therefore, the probability
For (vi)
The formula for finding the probability
Substitute 120 for ‘Frequency for the class N and B’ and 1,000 for ‘Total frequencies in the distribution’,
Therefore, the probability
b.
Check whether there is evidence that smoking and race are not independent or not. Explain the reason.
Answer to Problem 94CE
Yes, there is evidence that smoking and race are not independent because
Explanation of Solution
Calculation:
Special law of multiplication:
If two events A and B are independent, then
Consider smoking type smoker and race type as white.
From part (a),
The formula for checking independence is,
Consider smoking type smoker and race type as black.
The formula for checking independence is,
Here, it is observed that
c.
Check whether the given smoking rates shown here correspond to the person experience.
Answer to Problem 94CE
Yes, the given smoking rates shown here correspond to the person experience.
Explanation of Solution
Answers may vary: one of the answers is given below.
In experience, it is found that smoking has great influence on the racing.
Also in part (b), it is observed that the smoking and race are dependent. That is smoking is influencing the race. Thus, both experience and the smoking rates tells that same.
Therefore, the given smoking rates shown here correspond to the person experience.
d.
Explain the reason for public health officials are interested in the given type of data.
Explanation of Solution
From part (b), it can be observed that the smoking is dependent on race.
Here, the public health officials will design the special programs for the given types of data when the smoking is dependent on race.
Want to see more full solutions like this?
Chapter 5 Solutions
APPLIED STAT.IN BUS.+ECONOMICS
- Let X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).arrow_forwardA well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forward5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forward
- 8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward
- 9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage





