Chapter 5, Problem 86E

a.

To determine

Draw the scatterplot of the proportion of failing versus the load on the fabric.

Answer to Problem 86E

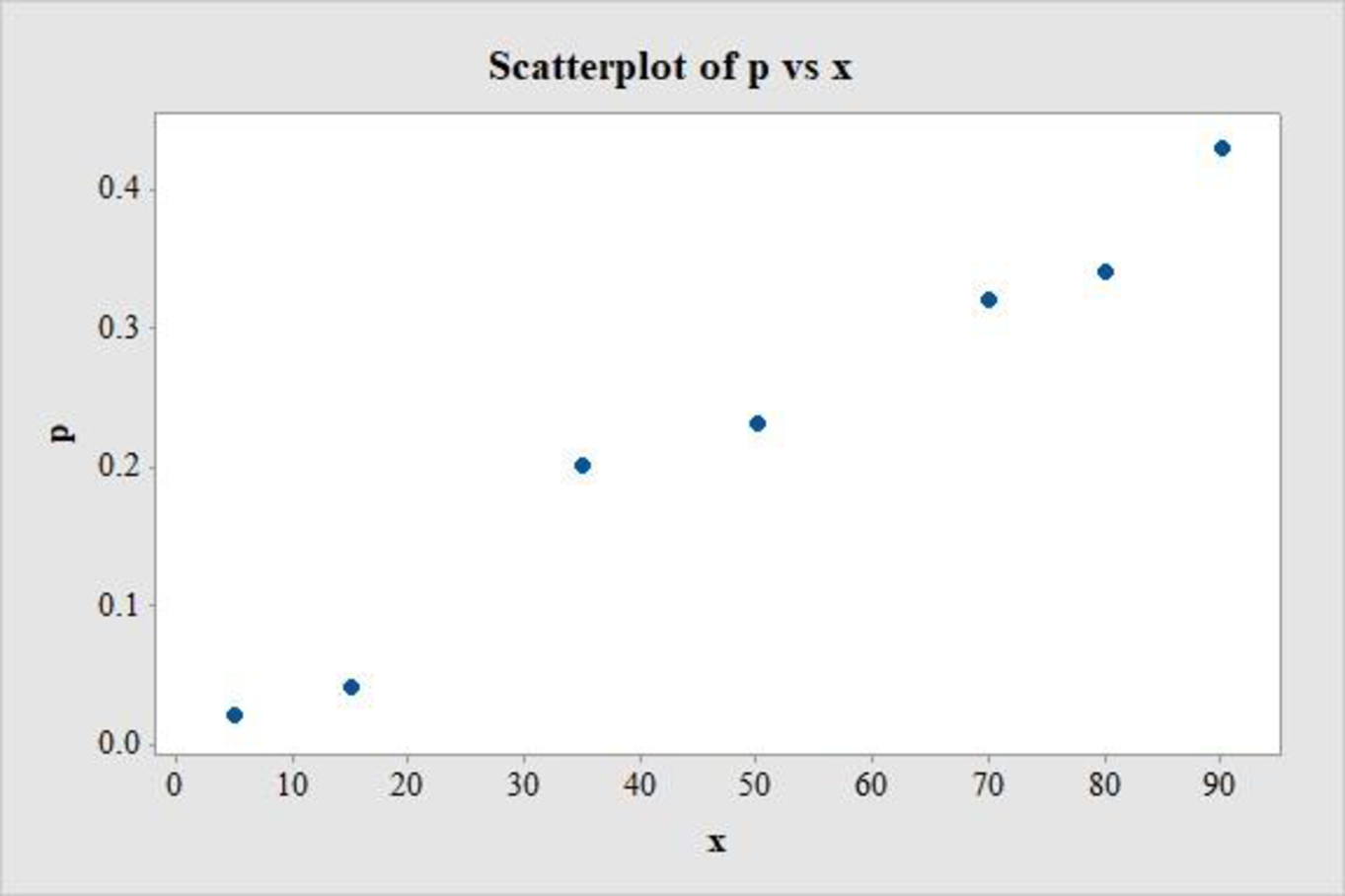
The scatterplot of the proportion of failing versus the load on the fabric is as follows:

Explanation of Solution

Calculation:

The given data relates the proportion of times a fabric fails, or causes a “wardrobe malfunction” with the load or force applied on it (lb/sq in.).

Denote the proportion of times a fabric fails as p and the load as x.

Scatterplot:

Software procedure:

Step-by-step procedure to draw the scatterplot using MINITAB software is given below:

• Choose Graph > Scatterplot.
• Choose Simple, and then click OK.
• Enter the column of p under Y variables.
• Enter the column of x under X variables.
• Click OK in all dialogue boxes.

Thus, the scatterplot for the data is obtained.

b.

To determine

Find the value of $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ for each load.

Fit a regression line of the form $y^{\prime }=a+b\left(\text{Load}\right)$.

Describe the significance of the positive slope.

Answer to Problem 86E

The regression line fitted to the given data is $\underset{\_}{y^{\prime }=1.513-0.5872x}$.

Explanation of Solution

Calculation:

Logistic regression:

The logistic regression equation for the prediction of a probability for the given value of the explanatory variable, x, is $\widehat{p}=\frac{e^{a+bx}}{1+e^{a+bx}}$, for constants a and b. For the logistic regression, $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ has a linear relationship with x, by the relation: $y^{\prime }=a+bx$.

The values of $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ can be obtained using software. Now, the proportion of failure of a fabric is p. In MINITAB, denote the column of $y^{\prime }$ as y*, so that $y*=\ln \left(\frac{p}{1-p}\right)$.

Data transformation $y*=\ln \left(\frac{p}{1-p}\right)$:

Software procedure:

Step-by-step procedure to transform the data using MINITAB software is given below:

• Choose Calc > Calculator.
• Enter the column of y* under Store result in variable.
• Enter the formula LN(‘p’/(1–‘p’)) under Expression.
• Click OK.

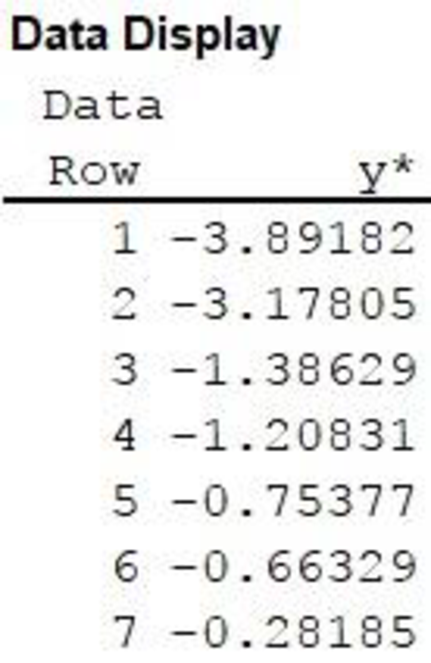
The transformed variable is stored in the column y*.

Data display:

Software procedure:

Step by step procedure to display the data using MINITAB software is given as,

• Choose Data > Display Data.
• Under Column, constants, and matrices to display, enter the column of y*.
• Click OK on all dialogue boxes.

The output using MINITAB software is given as follows:

Regression equation:

Software procedure:

Step by step procedure to obtain the regression equation using the MINITAB software:

• Choose Stat > Regression > Regression > Fit Regression Model.
• Enter the column of y* under Responses.
• Enter the columns of x under Continuous predictors.
• Choose Results and select Analysis of Variance, Model Summary, Coefficients, Regression Equation.
• Click OK in all dialogue boxes.

Output obtained using MINITAB is given below:

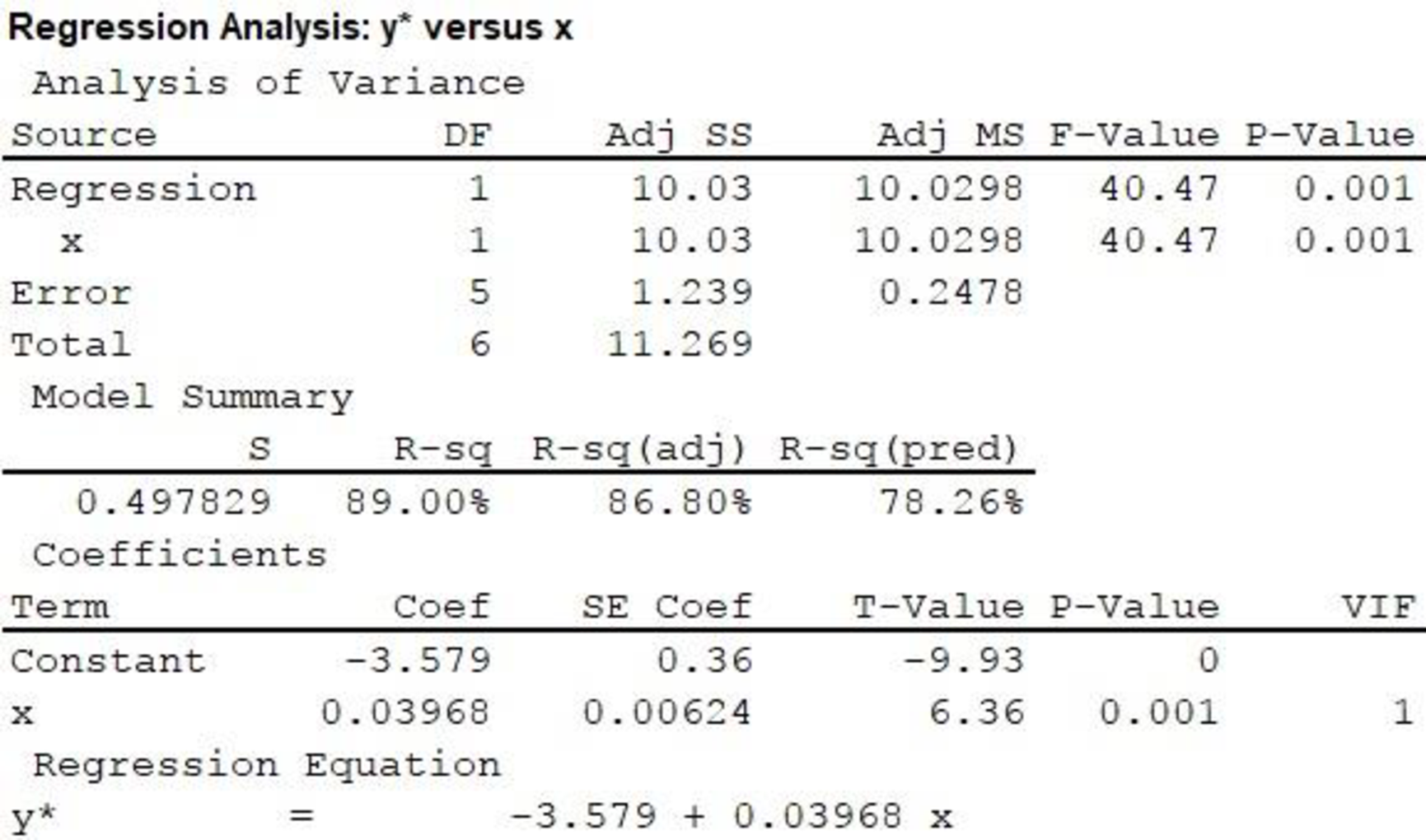
In the output, substituting $y*=y^{\prime }\left[=\ln \left(\frac{p}{1-p}\right)\right]$, the regression equation of the given form is $\underset{\_}{y^{\prime }=-3.579+0.03968x}$.

It is observed that the slope of x is 0.03968, which is positive. A positive slope implies that an increase in x causes an increase in yꞌ.

Now, it is known that the quantity $\frac{p}{1-p}$ is the odds of failure of a fabric, for a given load and $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ is the natural logarithm of odds. Moreover, it is known that logarithm is an increasing function of the variable.

In this case, an increase in load increases the natural logarithm of odds of failure, which, in turn, implies an increase in the odds of failure.

Thus, the positive slope implies that an increase in load causes an increase in the odds of failure of a fabric.

c.

To determine

Predict the proportion of failure of a fabric, for a load of 60 lb/sq in.

Answer to Problem 86E

The proportion of failure of a fabric, for a load of 60 lb/sq in. is 0.2318.

Explanation of Solution

Calculation:

For a load of 60 lb/sq in., substitute $x=60$ in the logistic equation:

$\begin{array}{c}{y}^{\prime }=-3.579+0.03968x\\ \ln \left(\frac{\widehat{p}}{1-\widehat{p}}\right)=-3.579+0.03968x\\ =-3.579+\left(0.03968\times 60\right)\\ =-3.579+2.3808\\ =-1.1982\end{array}$

Thus,

$\begin{array}{c}\frac{\widehat{p}}{1-\widehat{p}}=e^{-1.1982}\\ \approx \mathrm{0.3017.}\\ \frac{1-\widehat{p}}{\widehat{p}}=\frac{1}{0.3017}\\ \frac{1}{\widehat{p}}-1\approx 3.3141\end{array}$

    $\begin{array}{c}\frac{1}{\widehat{p}}=1+3.3141\\ =4.3141\\ \widehat{p}=\frac{1}{4.3141}\\ \approx \mathrm{0.2318.}\end{array}$

Thus, the proportion of failure of a fabric, for a load of 60 lb/sq in. is 0.2318.

d.

To determine

Estimate the maximum safe load to have a less than 5% chance of failing or wardrobe malfunction.

Answer to Problem 86E

The maximum safe load to have a less than 5% chance of failing or wardrobe malfunction is 16 lb/sq in.

Explanation of Solution

Calculation:

For a 5% chance of failing, $\widehat{p}=0.05\left(=\frac{5}{100}\right)$. Substitute this value in the logistic equation:

$\begin{array}{c}{y}^{\prime }=-3.579+0.03968x\\ \ln \left(\frac{\widehat{p}}{1-\widehat{p}}\right)=-3.579+0.03968x\\ \ln \left(\frac{0.05}{1-0.05}\right)=-3.579+0.03968x\\ \ln \left(\frac{0.05}{0.95}\right)=-3.579+0.03968x\\ \ln \left(0.0526\right)\approx -3.579+0.03968x\\ -2.9444=-3.579+0.03968x.\end{array}$

Thus,

$\begin{array}{c}0.03968x=-2.9444+3.579\\ =0.6346\\ x=\frac{0.6346}{0.03968}\\ \approx 15.99\\ \approx 16.\end{array}$

As a result, the load for a proportion of failure of 0.05 is 16 lb/sq in.

Now, from the explanation in Part b, an increase in the load causes an increase in the odds of failure. Thus, an increase in load from 16 lb/sq in. would cause an increase in the proportion of failure, whereas a decrease in load from 16 lb/sq in. would cause a decrease in the proportion of failure.

Thus, the maximum safe load to have a less than 5% chance of failing or wardrobe malfunction is 16 lb/sq in.