Answered: A 5.0-kg block is pushed 3.0 m up a…

Related questions

Question

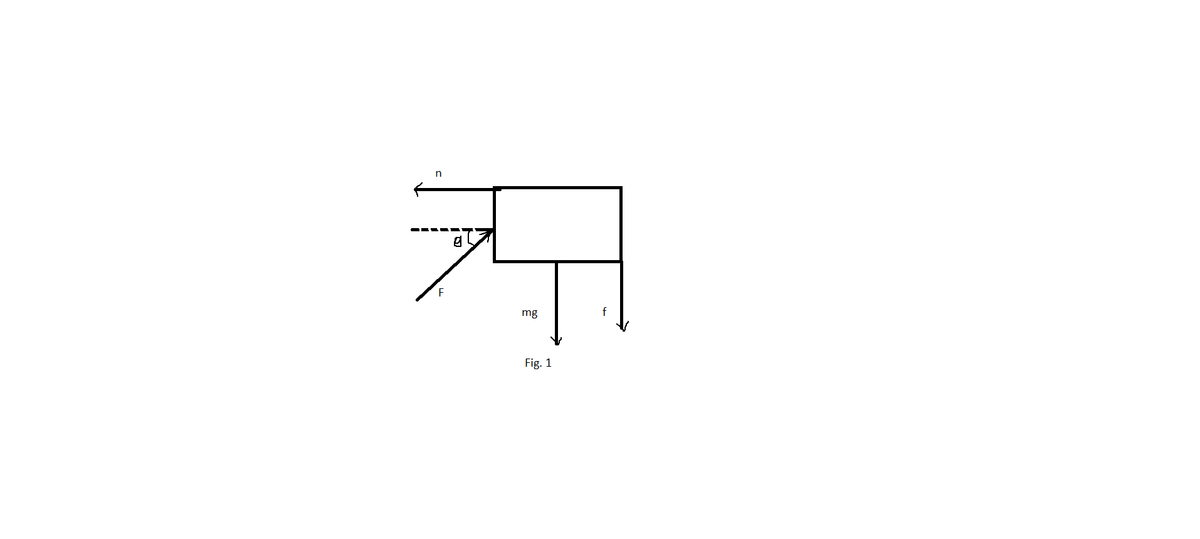
A 5.0-kg block is pushed 3.0 m up a vertical wall with constant speed by a constant force of magnitude F applied at an angle of θ = 30° with the horizontal, as shown in Figure P5.80. If the coefficient of kinetic friction between block and wall is 0.30, determine the work done by (a) width= , (b) the force of gravity, and (c) the normal force between block and wall. (d) By how much does the gravitational potential energy increase during the block’s motion?

FIGURE P5.80

Expert Solution

Step 1

$G i v e n t h a t, M a s s o f b l o c k (M) = 5 k g B l o c k i s p u s h e d v e r t i c a l l y u p w i t h d i s \tan c e = 3 m C o n s \tan t f o r c e i s a p p l i e d a t a n g l e (θ) = 30 ° C o e f f i c i e n t o f k i n e t i c f r i c t i o n (μ) = 0.30 H e r e, a : F o r f o r c e F : F r o m t h e F B D f i g . 1, w e c a n s a y t h a t d i f f e r e n t f o r c e s c a n a c t o n t h e b l o c k d i a g r a m : H e n c e, W e c a n a p p l y e q u i l i b r i u m c o n d i t i o n o n t h e f o r c e s a p p l i e d h o r i z o n t a l l y : S i n c e f r o m f i g . 1 : F \cos (θ) - n = 0 H e n c e, n = F \cos (θ) . . . . . . . . . . . . . . e q n 1 A s w e k n o w t h a t f r i c t i o n a l f o r c e c a n b e d e f i n e d a s : f = μ n . . . . . . . . . e q n 2 W h e r e, f = F r i c t i o n a l f o r c e μ = C o e f f i c i e n t o f f r i c t i o n a l F = F o r c e a p p l i e d o n t h e b l o c k n = N o r m a l f o r c e θ = A n g l e m a d e b y f o r c e a p p l i e d h o r i z o n t a l l y N o w, F r o m e q n 1 a n d e q n 2 : f = μ F \cos (θ) . . . . . . e q n 3 N o w f r o m t h e f i g . 1, W e c a n a p p l y e q u i l i b r i u m c o n d i t i o n o n t h e f o r c e s a p p l i e d v e r t i c a l l y : F \sin (θ) - m g - f = 0 . . . . . . . . e q n 4 H e r e p u t t i n g t h e v a l u e o f f i n e q n 4 : F \sin (θ) - m g - μ F \cos (θ) = 0 O n s o l v i n g a b o v e e q n : F = \frac{m g}{(\sin (θ) - μ F \cos (θ))} . . . . . . . . . e q n 5 A s w e k n o w t h a t, m = 5 k g g = 9.8 m / s e c^{2} θ = 30 ° μ = 0.30 P u t t i n g a l l t h e g i v e n v a l u e s i n e q n 5 : F = \frac{(5 k g) (9.8 m / s e c^{2})}{(\sin (30 °) - (0.30) F \cos (30 °))} F = 2 \times 10^{2} N . . . . . . . e q n 6$

Step 2

$A s w e k n o w t h a t, W o r k d o n e b y a c o n s \tan t f o r c e : W = F d \cos (ϕ) . . . . . . . . e q n 7 W h e r e, W = W o r k d o n e b y a c o n s \tan t f o r c e F = M a g n i t u d e o f f o r c e c o n s \tan t d = M a g n i t u d e o f d i s p l a c e m e n t ϕ = A n g l e b e t w e e n f o r c e a n d d i s p l a c e m e n t v e c t o r S i n c e, ϕ = 60 ° F = 2 \times 10^{2} N d = 3 m N o w p u t t i n g a l l v a l u e s i n e q n 7 : W = (2 \times 10^{2} N) (3 m) \cos (60 °) W = 3 \times 10^{2} J . . . . . . . e q n 8 A s w e k n o w t h a t f o r c e a n d i s p l a c e m e n t c a n n e v e r b e n e g a t i v e a n d h e n c e w o r k d o n e d e p e n d s o n t h e \cos θ w h e t h e r i t i s + v e o r - v e . A n s w e r : H e n c e, f r o m e q n 8, W o r k d o n e b y a p p l i e d f o r c e (\vec{F}) : W = 3 \times 10^{2} J$

Step by step

Solved in 4 steps with 1 images