
To find: The name of the person that records the fake data and write method to solve.
The faked data is recorded by Pat. Form an expression for
Given information: The figure is given as follows:
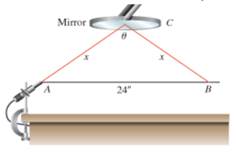
Figure (1)
Formula used: The law of cosine for a triangle
is given as follows:
Calculation:
Apply the law of cosine in
Further simplify the above equation.
Consider the positive value of
Substitute different values of
From the above table, it can be observed that the data matches with the values recorded by the Carmen. So, Carmen recorded the correct data.
Thus, the faked data is recorded by Pat. Form an expression for
Chapter 5 Solutions
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
- Suppose that f(x, y, z) = (x − 2)² + (y – 2)² + (z − 2)² with 0 < x, y, z and x+y+z≤ 10. 1. The critical point of f(x, y, z) is at (a, b, c). Then a = b = C = 2. Absolute minimum of f(x, y, z) is and the absolute maximum isarrow_forwardThe spread of an infectious disease is often modeled using the following autonomous differential equation: dI - - BI(N − I) − MI, dt where I is the number of infected people, N is the total size of the population being modeled, ẞ is a constant determining the rate of transmission, and μ is the rate at which people recover from infection. Close a) (5 points) Suppose ẞ = 0.01, N = 1000, and µ = 2. Find all equilibria. b) (5 points) For the equilbria in part a), determine whether each is stable or unstable. c) (3 points) Suppose ƒ(I) = d. Draw a phase plot of f against I. (You can use Wolfram Alpha or Desmos to plot the function, or draw the dt function by hand.) Identify the equilibria as stable or unstable in the graph. d) (2 points) Explain the biological meaning of these equilibria being stable or unstable.arrow_forwardFind the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forward
- Find the indefinite integral. Check Answer: In(5x) dx xarrow_forwardFind the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardHere is a region R in Quadrant I. y 2.0 T 1.5 1.0 0.5 0.0 + 55 0.0 0.5 1.0 1.5 2.0 X It is bounded by y = x¹/3, y = 1, and x = 0. We want to evaluate this double integral. ONLY ONE order of integration will work. Good luck! The dA =???arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





