
Concept explainers
Two blocks of masses m1 and m2, are placed on a table in contact with each other as discussed in Example 5.7 and shown in Figure 5.13a. The coefficient of kinetic friction between the block of mass m1 and the table is μ1, and that between the block of mass m2 and the table is μ2. A horizontal force of magnitude F is applied to the block of mass m1. We wish to find P, the magnitude of the contact force between the blocks. (a) Draw diagrams showing the forces for each block. (b) What is the net force on the system of two blocks? (c) What is the net force acting on m1? (d) What is the net force acting on m2? (e) Write Newton’s second law in the x direction for each block. (f) Solve the two equations in two unknowns for the acceleration a of the blocks in terms of the masses, the applied force F, the coefficients of friction, and g. (g) Find the magnitude P of the contact force between the blocks in terms of the same quantities.
(a)
The free body diagram of each block with forces.
The free body diagram of an object represents the direction and magnitude of forces acting on the body.
Explanation of Solution
The mass of block
The free body diagram of the book is given below.
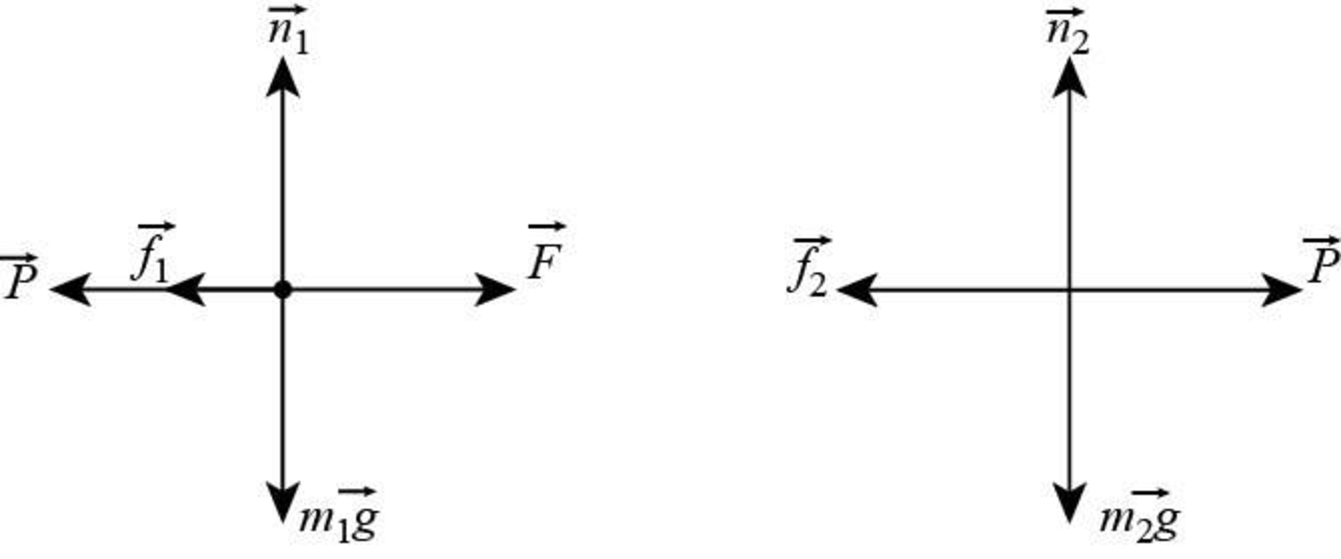
Figure (1)
The sum of all vertical forces is zero because the block moves on a horizontal surface. So the vertical acceleration,
Write the net force in the y-direction for mass
Here,
Write the net force in the y-direction for mass
Here,
Write the equation for kinetic friction for block
Here,
Write the equation for kinetic friction for block
Here,
In the figure,
Conclusion:
Therefore, the free body diagram of each block to show the forces is given in figure I.
(b)
The net force on the system of two blocks.
Answer to Problem 5.79AP
The net force on the system of two blocks is the external force applied minus the frictional force.
Explanation of Solution
Write the expression for the net force in x-direction for the system of two blocks from the figure I,
Here,
Conclusion:
Therefore, the net force on the system of two blocks is the external force applied minus the frictional force.
(c)
The net force acting on
Answer to Problem 5.79AP
The net force acting on
Explanation of Solution
Write the expression for the net force in x-direction for the system of two blocks from the figure I,
Here,
Conclusion:
Therefore, the net force acting on
(d)
The net force acting on
Answer to Problem 5.79AP
The net force acting on
Explanation of Solution
Write the expression for the net force in x-direction for the system of two blocks from the figure I,
Here,
Conclusion:
Therefore, the net force acting on
(e)
The Newton’s second law in the
Answer to Problem 5.79AP
The Newton’s second law in the
Explanation of Solution
The block has on a horizontal acceleration
Write the Newton’s second law for block
Substitute
Substitute
Write the Newton’s second law for block
Substitute
Substitute
Conclusion:
Therefore, the Newton’s second law in the
(f)
The acceleration of the blocks.
Answer to Problem 5.79AP
The acceleration of the blocks is
Explanation of Solution
Write the Newton’s second law is for block
Write the Newton’s second law is for block
Conclusion:
Add the equation (I) and equation (II) and solve for
Therefore, the acceleration of the blocks is
(g)
The magnitude of the contact force between the blocks in terms of acceleration, mass, applied force and the friction coefficient.
Answer to Problem 5.79AP
The magnitude
Explanation of Solution
Recall the equation (II).
Substitute
Conclusion:
Therefore, the magnitude
Want to see more full solutions like this?
Chapter 5 Solutions
Physics for Scientists and Engineers, Volume 1
- 1.) Two long parallel current-carrying wires P and Q are separated by 0.10 m. The current in wire P is 5.0 A. The magnetic force on a length of 0.50 m of wire P due to the current in wire Q is 2.0 × 10-s N. (a) State and explain the magnitude of the force on a length of 0.50 m of wire Q due to the current in P. [2] (b) Calculate the current in wire Q. [2] (c) Another current-carrying wire R is placed parallel to wires P and Q and halfway between them as shown. wire P wire R wire Q 0.05 m 0.05 m The net magnetic force on wire Q is now zero. (c.i) State the direction of the current in R, relative to the current in P.[1] (c.ii) Deduce the current in R. [2]arrow_forward2.) A 50.0 resistor is connected to a cell of emf 3.00 V. The voltmeter and the ammeter in the circuit are ideal. V A 50.00 (a) The current in the ammeter is 59.0 mA. Calculate the internal resistance of the cell. The circuit is changed by connecting another resistor R in parallel to the 50.0 resistor. V A 50.00 R (b) Explain the effect of this change on R is made of a resistive wire of uniform cross-sectional area 3.1 × 10-8 m², resistivity 4.9 × 10-70m and length L. The resistance of R is given by the equation R = KL where k is a constant. (b.i) the reading of the ammeter. [2] (b.ii) the reading of the voltmeter. [2] (c) Calculate k. State an appropriate unit for your answer. [3] [2]arrow_forwardNo chatgpt pls will upvotearrow_forward
- No chatgpt pls will upvotearrow_forwardA rod 12.0 cm long is uniformly charged and has a total charge of -20.0 μc. Determine the magnitude and direction of the electric field along the axis of the rod at a point 32.0 cm from its center. 361000 ☑ magnitude What is the general expression for the electric field along the axis of a uniform rod? N/C direction toward the rodarrow_forwardA certain brand of freezer is advertised to use 730 kW h of energy per year. Part A Assuming the freezer operates for 5 hours each day, how much power does it require while operating? Express your answer in watts. ΜΕ ΑΣΦ ? P Submit Request Answer Part B W If the freezer keeps its interior at a temperature of -6.0° C in a 20.0° C room, what is its theoretical maximum performance coefficient? Enter your answer numerically. K = ΜΕ ΑΣΦ Submit Request Answer Part C What is the theoretical maximum amount of ice this freezer could make in an hour, starting with water at 20.0°C? Express your answer in kilograms. m = Ο ΑΣΦ kgarrow_forward
- Describe the development of rational choice theory in sociology. Please includearrow_forwardA-E pleasearrow_forwardA 11.8 L gas tank containing 3.90 moles of ideal He gas at 26.0°C is placed inside a completely evacuated insulated bell jar of volume 39.0 L .A small hole in the tank allows the He to leak out into the jar until the gas reaches a final equilibrium state with no more leakage. Part A What is the change in entropy of this system due to the leaking of the gas? ■ ΜΕ ΑΣΦ AS = ? J/K Submit Request Answer Part B Is the process reversible or irreversible?arrow_forward
- A-E pleasearrow_forwardThree moles of an ideal gas undergo a reversible isothermal compression at 20.0° C. During this compression, 1900 J of work is done on the gas. For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Entropy change in a free expansion. Part A What is the change of entropy of the gas? ΤΕ ΑΣΦ AS = Submit Request Answer J/Karrow_forward5.97 Block A, with weight 3w, slides down an inclined plane S of slope angle 36.9° at a constant speed while plank B, with weight w, rests on top of A. The plank is attached by a cord to the wall (Fig. P5.97). (a) Draw a diagram of all the forces acting on block A. (b) If the coefficient of kinetic friction is the same between A and B and between S and A, determine its value. Figure P5.97 B A S 36.9°arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





