
Concept explainers
Area functions and the Fundamental Theorem Consider the function
and its graph shown below.
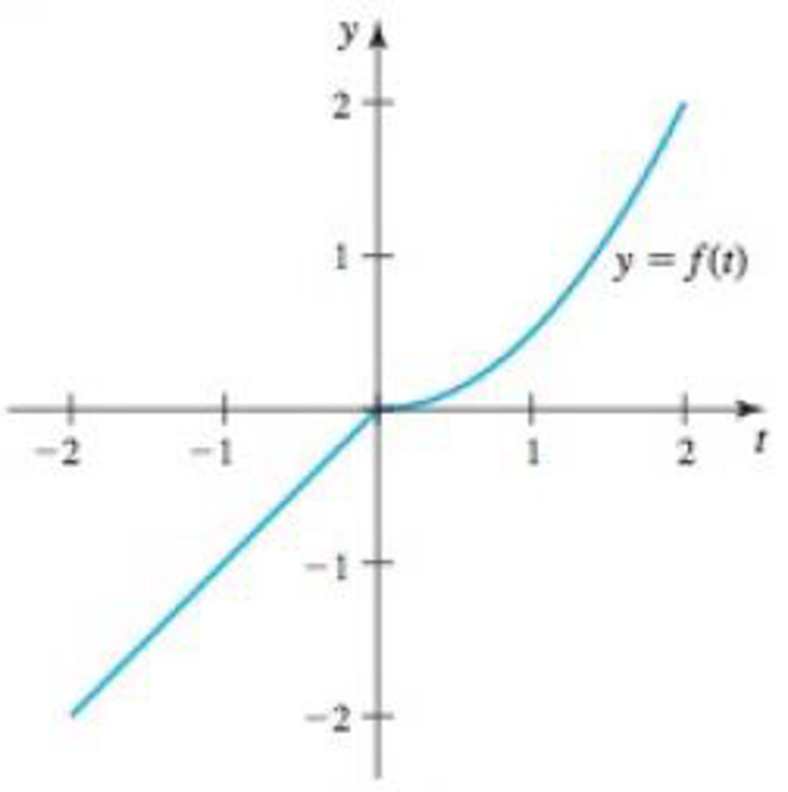
Let
56.
- a. Evaluate G(−1) and G(1).
- b. Use the Fundamental Theorem to find an expression for G′(x), for −2 ≤ x ≤ 0.
- c. Use the Fundamental Theorem to find an expression for G′(x), for 0 ≤ x ≤ 2.
- d. Evaluate G′(0) and G′(1). Interpret these values.
- e. Find a constant C such that F(x) = G(x) + C.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Calculus: Early Transcendentals, 2nd Edition
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Introductory Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- Example: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardPlease can you give detailed steps on how the solutions change from complex form to real form. Thanks.arrow_forward
- Examples: Solve the following differential equation using Laplace transform (e) ty"-ty+y=0 with y(0) = 0, and y'(0) = 1arrow_forwardExamples: Solve the following differential equation using Laplace transform (a) y" +2y+y=t with y(0) = 0, and y'(0) = 1arrow_forwardπ 25. If lies in the interval <0arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
