Mathematical Applications for the Management, Life, and Social Sciences
11th Edition
ISBN: 9781305108042
Author: Ronald J. Harshbarger, James J. Reynolds
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 5, Problem 54RE
To determine
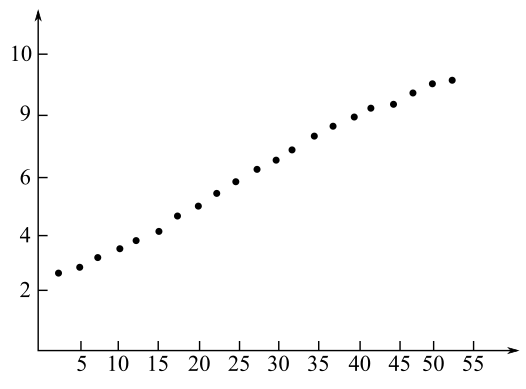
Whether the graph of world population (in billion) in 5 years increments from 1950 to 2025 (x=0 in 1945) is a growth exponential, decay exponential, or logarithmic by observing the provided graph,
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the absolute extrema of the function f(x, y) = x² + y² - 3x-3y+3 on the domain defined by
x² + y² <9.
Round answers to 3 decimals or more.
Absolute Maximum:
Absolute Minimum:
Find the maximum and minimum values of the function f(x, y) = e² subject to ï³ + y³ = 128
Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist.
Maximum value:
A chemical manufacturing plant can produce x units of chemical Z given p units of chemical P and 7 units
of chemical R, where:
z = 140p0.6,0.4
Chemical P costs $300 a unit and chemical R costs $1,500 a unit. The company wants to produce as many
units of chemical Z as possible with a total budget of $187,500.
A) How many units each chemical (P and R) should be "purchased" to maximize production of chemical Z
subject to the budgetary constraint?
Units of chemical P, p =
Units of chemical R, r =
B) What is the maximum number of units of chemical Z under the given budgetary conditions? (Round your
answer to the nearest whole unit.)
Max production, z=
units
Chapter 5 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
Ch. 5.1 - 1. Can any value of x give a negative value for y...Ch. 5.1 - 2. If , what asymptote does the graph of ...Ch. 5.1 - Prob. 3CPCh. 5.1 - Prob. 4CPCh. 5.1 - Prob. 5CPCh. 5.1 - Prob. 6CPCh. 5.1 - Prob. 1ECh. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - Prob. 4E
Ch. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - Prob. 9ECh. 5.1 - Prob. 10ECh. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - 23. (a) Graph .
(b) Graph .
(c) Algebraically show...Ch. 5.1 - Prob. 20ECh. 5.1 - 25. Given that , write an equivalent equation in...Ch. 5.1 - 26. Given that , write an equivalent equation in...Ch. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - 33. Compound interest If $1000 is invested for x...Ch. 5.1 - 35. Compound interest We will show in the next...Ch. 5.1 - 36. Compound interest If $1000 is invested for x...Ch. 5.1 - 37. Drug in the bloodstream The percent...Ch. 5.1 - Bacterial growth A single bacterium splits into...Ch. 5.1 - 39. Product reliability A statistical study shows...Ch. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - Prob. 38ECh. 5.1 - 46. Advertising and sales Suppose that sales are...Ch. 5.1 - 47. Modeling Carbon dioxide emissions The...Ch. 5.1 - 53. Modeling Alzheimer’s disease As the baby...Ch. 5.2 - 1. What asymptote does the graph of approach when...Ch. 5.2 - 2. For , does the equation represent the same...Ch. 5.2 - Prob. 3CPCh. 5.2 - Prob. 4CPCh. 5.2 - 5. Simplify:
(a) (b) (c) (d) log 1
Ch. 5.2 - Prob. 6CPCh. 5.2 - In Problems 1-4, use the definition of a...Ch. 5.2 - Prob. 2ECh. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - In Problems 5-14, solve for x by writing the...Ch. 5.2 - In Problems 5-14, solve for x by writing the...Ch. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - In Problems 19 and 20, write the equation in...Ch. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - In Problems 27 and 28, use properties of...Ch. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - In Problems 35 and 36, evaluate each logarithm...Ch. 5.2 - In Problems 35 and 36, evaluate each logarithm...Ch. 5.2 - Write each expression in Problems 37-40 as the sum...Ch. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Write each expression in Problems 37-40 as the sum...Ch. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - In Problems 45-48, use a calculator to determine...Ch. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Richter scale Use the formula in Problems 59-62....Ch. 5.2 - Richter scale Use the formula in Problems 59-62....Ch. 5.2 - Prob. 61ECh. 5.2 - Richter scale Use the formula in Problems 59-62....Ch. 5.2 - Prob. 63ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Doubling time In Problems 71 and 72, use the...Ch. 5.2 - Prob. 72ECh. 5.2 - 73. Women in the workforce For selected years from...Ch. 5.2 - 75. Modeling Diabetes As the following table...Ch. 5.2 - Prob. 76ECh. 5.2 - 78. Modeling Demographics The table below gives...Ch. 5.3 - 1. Suppose the sales of a product, in dollars, are...Ch. 5.3 - 2. Suppose the monthly demand for a product is...Ch. 5.3 - 3. Suppose the number of employees at a new...Ch. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - In Problems 1-22, solve each equation. Give...Ch. 5.3 - In Problems 1-22, solve each equation. Give...Ch. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - In Problems 1-22, solve each equation. Give...Ch. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - 25. Sales decay The sales decay for a product is...Ch. 5.3 - 26. Sales decay The sales of a product decline...Ch. 5.3 - 27. Inflation The purchasing power P (in dollars)...Ch. 5.3 - 28. Product reliability A statistical study shows...Ch. 5.3 - 29. Radioactive half-life An initial amount of 100...Ch. 5.3 - 30. Radioactive half-life A breeder reactor...Ch. 5.3 - 31. Population growth If the population of a...Ch. 5.3 - 32. Population growth The population of a certain...Ch. 5.3 - 35. Demand The demand function for a certain...Ch. 5.3 - 36. Demand The demand function for a product is...Ch. 5.3 - 37. Supply If the supply function for a product is...Ch. 5.3 - Prob. 38ECh. 5.3 - 39. Total cost The total cost function for x units...Ch. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - 43. Compound interest If $8500 is invested at...Ch. 5.3 - 44. Compound interest If $1000 is invested at 10%...Ch. 5.3 - 45. Compound interest If $5000 is invested at 9%...Ch. 5.3 - Prob. 46ECh. 5.3 - Profits An investment services company experienced...Ch. 5.3 - Profits An investment services company experienced...Ch. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - 51. Supply Suppose the supply of x units of a...Ch. 5.3 - 52. Demand Assume that the demand function for a...Ch. 5.3 - 53. Sales growth The president of a company...Ch. 5.3 - Prob. 54ECh. 5.3 - 55. Organizational growth Suppose that the...Ch. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - 58. Population growth Suppose that the number y of...Ch. 5.3 - 59. Spread of disease On a college campus of...Ch. 5.3 - 60. Spread of a rumor The number of people N(t) in...Ch. 5.3 - 61. Market share Suppose that the market share y...Ch. 5.3 - 62. Advertising An advertising agency has found...Ch. 5.3 - 63. Pollution Pollution levels in a lake have been...Ch. 5.3 - 64. Fish length Suppose that the length x (in...Ch. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - 67. Modeling Diabetes The following table gives...Ch. 5 - 1. Write each statement in logarithmic form.
Ch. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - In Problems 13-20, evaluate each logarithm without...Ch. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - In Problems 13-20, evaluate each logarithm without...Ch. 5 - In Problems 13-20, evaluate each logarithm without...Ch. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - In Problems 21-24, if , find each of the following...Ch. 5 - In Problems 21-24, if , find each of the following...Ch. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - 27. Is it true that ln for all positive values of...Ch. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - 31. If
Ch. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - In Problems 36-42, solve each equation.
37.
Ch. 5 - Prob. 38RECh. 5 - In Problems 36-42, solve each equation.
39.
Ch. 5 - In Problems 36-42, solve each equation.
40.
Ch. 5 - Prob. 41RECh. 5 - In Problems 36-42, solve each equation.
42.
Ch. 5 - Prob. 43RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - 50. Sales decay The sales decay for a product is...Ch. 5 - Prob. 51RECh. 5 - 54. Compound interest If $1000 is invested at 12%,...Ch. 5 - 55. Compound interest If $5000 is invested at...Ch. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 1TCh. 5 - Prob. 2TCh. 5 - Prob. 3TCh. 5 - Prob. 4TCh. 5 - Prob. 5TCh. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - Prob. 9TCh. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - Prob. 12TCh. 5 - Prob. 13TCh. 5 - Prob. 14TCh. 5 - Prob. 15TCh. 5 - Prob. 16TCh. 5 - Prob. 17TCh. 5 - Prob. 18TCh. 5 - Prob. 19TCh. 5 - Prob. 20TCh. 5 - Prob. 21TCh. 5 - Prob. 22TCh. 5 - Prob. 23TCh. 5 - Prob. 24TCh. 5 - Prob. 25TCh. 5 - Prob. 26TCh. 5 - 27. The total national health expenditures per...Ch. 5 - 28. A company plans to phase out one model of its...Ch. 5 - Prob. 30T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A firm manufactures a commodity at two different factories, Factory X and Factory Y. The total cost (in dollars) of manufacturing depends on the quantities, and y produced at each factory, respectively, and is expressed by the joint cost function: C(x, y) = x² + xy +4y²+400 A) If the company's objective is to produce 1,900 units per month while minimizing the total monthly cost of production, how many units should be produced at each factory? (Round your answer to whole units, i.e. no decimal places.) To minimize costs, the company should produce: units at Factory X and units at Factory Y B) For this combination of units, their minimal costs will be enter any commas in your answer.) Question Help: Video dollars. (Do notarrow_forwarduse Lagrange multipliers to solvearrow_forwardSuppose a Cobb-Douglas Production function is given by the following: P(L,K)=80L0.75 K-0.25 where L is units of labor, K is units of capital, and P(L, K) is total units that can be produced with this labor/capital combination. Suppose each unit of labor costs $400 and each unit of capital costs $1,600. Further suppose a total of $384,000 is available to be invested in labor and capital (combined). A) How many units of labor and capital should be "purchased" to maximize production subject to your budgetary constraint? Units of labor, L = Units of capital, K = B) What is the maximum number of units of production under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production = unitsarrow_forward
- Suppose a Cobb-Douglas Production function is given by the function: P(L, K) = 7L0.0 K0.4 Furthemore, the cost function for a facility is given by the function: C(L, K) = 100L +400K Suppose the monthly production goal of this facility is to produce 15,000 items. In this problem, we will assume L represents units of labor invested and K represents units of capital invested, and that you can invest in tenths of units for each of these. What allocation of labor and capital will minimize total production Costs? Units of Labor L = Units of Capital K = (Show your answer is exactly 1 decimal place) (Show your answer is exactly 1 decimal place) Also, what is the minimal cost to produce 15,000 units? (Use your rounded values for L and K from above to answer this question.) The minimal cost to produce 15,000 units is $ Hint: 1. Your constraint equation involves the Cobb Douglas Production function, not the Cost function. 2. When finding a relationship between L and K in your system of equations,…arrow_forward1. Give a subset that satisfies all the following properties simultaneously: Subspace Convex set Affine set Balanced set Symmetric set Hyperspace Hyperplane 2. Give a subset that satisfies some of the conditions mentioned in (1) but not all, with examples. 3. Provide a mathematical example (not just an explanation) of the union of two balanced sets that is not balanced. 4. What is the precise mathematical condition for the union of two hyperspaces to also be a hyperspace? Provide a proof. edited 9:11arrow_forwardFind the absolute maximum and minimum of f(x, y) = x + y within the domain x² + y² ≤ 4. Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. 1. Absolute minimum of f(x, y) isarrow_forward
- Suppose that one factory inputs its goods from two different plants, A and B, with different costs, 3 and 7 each respective. And suppose the price function in the market is decided as p(x, y) = 100 - x - y where I and y are the demand functions and 0 < x,y. Then as x = y = the factory can attain the maximum profit,arrow_forward0|0|0|0 - Consider the time series X₁ and Y₁ = (I – B)² (I – B³)Xt. What transformations were performed on Xt to obtain Yt? seasonal difference of order 2 simple difference of order 5 seasonal difference of order 1 seasonal difference of order 5 simple difference of order 2arrow_forwardEvaluate the following integrals, showing all your workingarrow_forward
- Consider the function f(x) = 2x³-4x2-x+1. (a) Without doing a sketch, show that the cubic equation has at least one solution on the interval [0,1]. Use a theorem discussed in lectures, or see Section 1.8 of Calculus (7th ed) by Stewart. Ensure that the conditions of the theorem are satisfied (include this in your solution) (b) Now, by sketching the cubic (by hand or by computer), you should see that there is, in fact, exactly one zero in the interval [0,1]. Use Newton's method to find this zero accurate to 3 decimal places. You should include a sketch of the cubic, Newton's iteration formula, and the list of iterates. [Use a computer if possible, e.g., a spreadsheet or MatLab.]arrow_forwardEvaluate the following integrals, showing all your workingarrow_forwardDifferentiate the following functionarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY