Chapter 5, Problem 5.1CP

To determine

To rewrite:

This function in dimensionless form, using dimensional analysis.

Answer to Problem 5.1CP

The dimensionless function is $C_f=fcn(\mathrm{Re},\frac{\epsilon }{d})$

Explanation of Solution

Given Information:

For long circular rough pipes in turbulent flow, wall shear ${\tau }_w$ is a function of density $\rho$, viscosity $\mu$ .average velocity V, pipe diameter d and wall roughness height e. Thus it can be written as:

${\tau }_w=fcn(\rho ,\mu ,V,d,e)$

Concept Used:

The number of pi groups are to be calculated:

$N=k-r$

Where k is the number of variables and r is the number of fundamental references.

On substituting 6 for k and 3 for r ,

$N=3$

Calculation:

Dimensional analysis is applied to find the pi groups.

First pi group:

${\pi }_1={\rho }^a{V}^b{\mu }^{c}d$

Where $\rho$ is the density, velocity is V, diameter is d and the dynamic viscosity is $\mu$.

On substituting $M^0{L}^0{T}^0$ for ${\pi }_1$, $[M{L}^{-3}]$ for $\rho$, $[L{T}^{-1}]$ for V and $[M{L}^{-1}{T}^{-1}]$ for $\mu$,

$M^0{L}^0{T}^0={[M{L}^{-3}]}^a{[L{T}^{-1}]}^b{[M{L}^{-1}{T}^{-1}]}^c[L]$

$M^0{L}^0{T}^0=[M^{a+c}{L}^{-3a+b-c+1}{T}^{-b-c}]$

On equating M coefficients:

$\begin{array}{l}a+c=0\\ a=-c\end{array}$

On equating T coefficients:

$\begin{array}{l}-b-c=0\\ b=-c\end{array}$

On equating L coefficients:

$\begin{array}{l}-3a+b-c+1=0\\ -3(-c)+(-c)-c+1=0\\ c=-1\end{array}$

Hence, a = 1, b = 1

Therefore, the first pi group is as follows:

${\pi }_1={\rho }^1{V}^1{\mu }^{-1}d$

${\pi }_1=\frac{\rho Vd}{\mu }$

Second pi group:

${\pi }_2={\rho }^a{V}^b{\epsilon }^{c}d$

Where $\rho$ is the density, velocity is V, diameter is d and roughness height is $\epsilon$.

On substituting $M^0{L}^0{T}^0$ for ${\pi }_2$, $[M{L}^{-3}]$ for $\rho$, $[M^0{L}^1{T}^0]$ for $\epsilon$ and L for d ,

$M^0{L}^0{T}^0={[M{L}^{-3}]}^a{[L{T}^{-1}]}^b{[M^0{L}^1{T}^0]}^c[L]$

$M^0{L}^0{T}^0=[M^a{L}^{-3a+b+c+1}{T}^{-b}]$

On equating M coefficients:

$a=0$

On equating T coefficients:

$\begin{array}{l}-b=0\\ b=0\end{array}$

On equating L coefficients:

$\begin{array}{l}-3a+b+c-1=0\\ -3(0)+0+c-1=0\\ c=1\end{array}$

Therefore, the second pi group is as follows:

${\pi }_2={\rho }^0{V}^0{\epsilon }^1{d}^{-1}$

${\pi }_2=\frac{\epsilon }{d}$

Third pi group:

${\pi }_3={\rho }^a{V}^b{d}^c{\tau }_w$

Where $\rho$ is the density, velocity is V, diameter is d and shear stress is ${\tau }_w$.

On substituting $M^0{L}^0{T}^0$ for ${\pi }_3$, $[M{L}^{-3}]$ for $\rho$, $[L{T}^{-1}]$ for V, $[L]$ for d, and $[M{L}^{-1}{T}^{-2}]$ for ${\tau }_w$,

$M^0{L}^0{T}^0={[M{L}^{-3}]}^a{[L{T}^{-1}]}^b{[L]}^c[M{L}^{-1}{T}^{-2}]$

$M^0{L}^0{T}^0=[M^{a+1}{L}^{-3a+b+c-1}{T}^{-b-2}]$

On equating M coefficients:

$\begin{array}{l}a+1=0\\ a=-1\end{array}$

On equating T coefficients:

$\begin{array}{l}-b-2=0\\ b=-2\end{array}$

On equating L coefficients:

$\begin{array}{l}-3a+b+c-1=0\\ -3(-1)+(-2)+c-1=0\\ c=0\end{array}$

Therefore, the third pi group is as follows:

${\pi }_3={\rho }^{-1}{V}^{-2}{d}^0{\tau }_w$

${\pi }_2=\frac{{\tau }_w}{\rho V^2}$

Hence as per the choices:

${\pi }_3=fcn({\pi }_1,{\pi }_2)$

On substituting $\frac{{\tau }_w}{\rho V^2}$ for ${\pi }_3$, $\frac{\epsilon }{d}$ for ${\pi }_2$ and $\frac{\rho Vd}{\mu }$ for ${\pi }_1$,

$\frac{{\tau }_w}{\rho V^2}=fcn(\frac{\rho Vd}{\mu },\frac{\epsilon }{d})$

Where $\frac{{\tau }_w}{\rho V^2}$ is the skin friction coefficient represented by C_f and $\frac{\rho Vd}{\mu }$ is known as Reynolds number represented by Re.

$C_f=fcn(\mathrm{Re},\frac{\epsilon }{d})$

Conclusion:

The dimensionless function is $C_f=fcn(\mathrm{Re},\frac{\epsilon }{d})$.

To determine

To plot:

Data using the dimensionless form obtained, a curve fit formula and a single value of a range.

Answer to Problem 5.1CP

The data is plotted as above, the curve fit formula is $C_f=3.63{\mathrm{Re}}^{-0.64}$ and the curve is valid for only Reynolds number range of 2000-22000 and single $\epsilon /d$ value.

Explanation of Solution

Given Information:

Diameter of pipe, d = 5 cm

$\epsilon =0.25mm$

The following values of wall shear stress are shown by the measurements for flow of water at 20?:

Concept Used:

The parameter $\epsilon /d$ remains constant for all data.

As per the table (Moody chart):

$\mu =0.001kg/m.s$, the dynamic viscosity of water at 20°C

$\rho =998kg/m^3$, the density of water at 20°C

The velocity is calculated as follows:

$V=\frac{Q}{A}$

$V=\frac{Q}{\frac{\pi }{4}{d}^2}$

Reynolds number is calculated as follows:

$\mathrm{Re}=\frac{\rho Vd}{\mu }$

The skin friction coefficient is calculated as follows:

$C_f=\frac{{\tau }_w}{\rho V^2}$

Calculation:

$\frac{\epsilon }{d}=\frac{0.25}{50}$, because parameter $\epsilon /d$ remains constant for all data.

On substituting 1.5 gal/min for Q and 50 mm for d in the calculation of velocity:

$V=\frac{1.5gal/\min \times (\frac{6.3094\times {10}^{-5}{m}^3/s}{1gal/\min })}{\frac{\pi }{4}{d}^2}$

$V=\frac{1.5gal/\min \times 6.3094\times {10}^{-5}{m}^3/s}{\frac{\pi }{4}{(50\times {10}^{-3})}^2{m}^2}$

$V=0.0481972m/s$

On substituting 998 kg/m³ for $\rho$, 0.0481972 m/s for V ,50 mm for d and 0.001 kg/m.s for $\mu$ in the calculation for Reynolds number:

$\mathrm{Re}=\frac{998\times 0.0481972\times (50\times {10}^{-3})}{\mu }$

$\mathrm{Re}=\frac{48.1008056\times (50\times {10}^{-3})}{0.001}$

$=2405$

On substituting 0.05 Pa for ${\tau }_w$, 998 kg/m³ for $\rho$ and 0.0481972 m/s for V.

$C_f=\frac{{\tau }_w}{998\times {0.0481972}^2}$

$C_f=\frac{0.05}{2.31832415}$

$=0.021567$

Remaining values are also calculated similarly and tabulated as follows:

V (m/s)	0.0481972	0.0963944	0.1927888	0.2891832	0.3855776	0.4498406
Re	2405	4810	9620	14430	19240	22447
Cf	0.021567	0.019411	0.009975	0.007668	0.005796	0.00619

The curve is plotted between C_f versus Re:

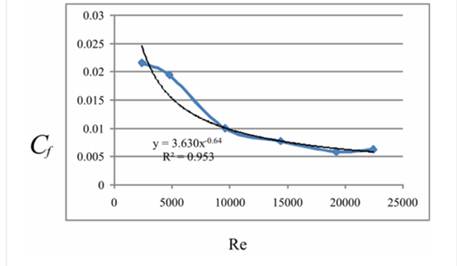
The following equation shows the power law curve fit in the plot:

$C_f=3.63{\mathrm{Re}}^{-0.64}$

$R^2=0.953$

Hence, 95.3% is the correlation.

Hence, the curve is valid for only Reynolds number range of 2000-22000 and single $\epsilon /d$ value.

Conclusion:

The data is plotted as above, the curve fit formula is $C_f=3.63{\mathrm{Re}}^{-0.64}$ and the curve is valid for only Reynolds number range of 2000-22000 and single $\epsilon /d$ value.