Chapter 5, Problem 5.143RP

The shaft is made of A992 steel and has an allowable shear stress of τ_allow = 75 MPa. When the shaft is rotating at 300 rpm, the motor supplies 8 kW of power, while gears A and B withdraw 5 kW and 3 kW, respectively. Determine the required minimum diameter of the shaft to the nearest millimeter. Also, find the rotation of gear A relative to C.

To determine

The required minimum diameter of the shaft.

The angle of twist of gear A relative to gear C.

Answer to Problem 5.143RP

The required minimum diameter of the shaft is $\underset{\_}{26\text{mm}}$.

The angle of twist of gear A relative to gear C is $\underset{\_}{2.11°}$.

Explanation of Solution

Given information:

The allowable shear stress in the shaft is 75 MPa.

The motor supplies power of 8 kW.

Gear A and B withdraws power of 5 kW and 3 kW.

Shaft rotates at 300 rpm.

Calculation:

The expression for the power transmitted $\left(P\right)$ by the shaft is shown below:

$P=T\omega$ (1)

Here, T is the applied torque and $\omega$ is the angular velocity of the shaft.

Rearrange Equation (1) to find the torque at A.

$T_A=\frac{P_A}{\omega }$ (2)

Here, $P_A$ is the power at gear A.

The expression for angular velocity of the shaft $\left(\omega \right)$ is shown below:

$\omega =2\pi f$ (3)

Here, f is the frequency of shaft’s rotation.

Substitute $300\frac{\text{rev}}{\min }$ for f in Equation (3).

$\begin{array}{c}\omega =2\pi \left(300\frac{\text{rev}}{\min }\right)\\ =2\pi \left(300\frac{\text{rev}}{\min }\times \frac{1\min }{60\sec }\right)\\ =31.4159\frac{\text{rad}}{\sec }\end{array}$

Substitute 5 kW for $P_A$ and $31.4159\frac{\text{rad}}{\sec }$ for $\omega$ in Equation (2).

$\begin{array}{c}{T}_A=\frac{5\text{kW}}{31.4159\frac{\text{rad}}{\sec }}\\ =\frac{5\text{kW}\left(\frac{{10}^3\text{W}}{1\text{kW}}\right)}{31.4159\frac{\text{rad}}{\sec }}\\ =159.15\text{N}\cdot \text{m}\end{array}$

Find the torque at C.

$T_C=\frac{P_C}{\omega }$ (4)

Here, $P_C$ is the power at gear C.

Substitute 8 kW for $P_C$ and $31.4159\frac{\text{rad}}{\sec }$ for $\omega$ in Equation (4).

$\begin{array}{c}{T}_C=\frac{8\text{kW}}{31.4159\frac{\text{rad}}{\sec }}\\ =\frac{8\text{kW}\left(\frac{{10}^3\text{W}}{1\text{kW}}\right)}{31.4159\frac{\text{rad}}{\sec }}\\ =254.65\text{N}\cdot \text{m}\end{array}$

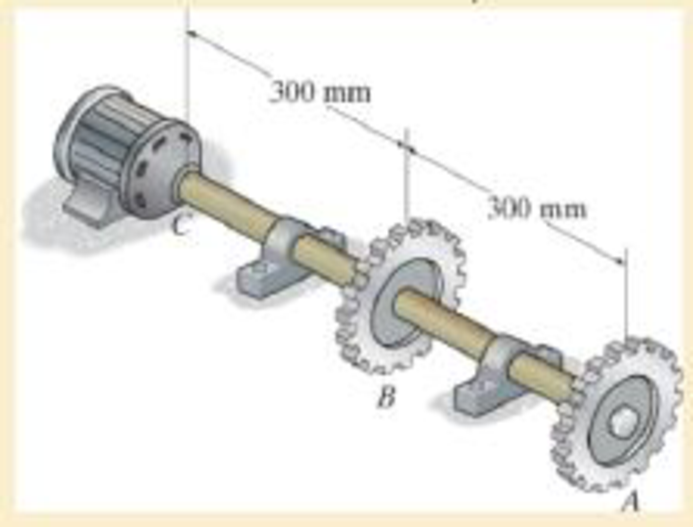
Sketch the internal torque in the segment BC of the shaft as shown in Figure 1.

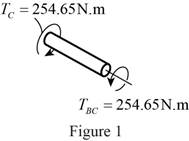
Sketch the internal torque in the segment AB of the shaft as shown in Figure 2.

Refer Figure 1 and Figure 2.

Segment BC of the shat is subjected to a greater internal torque of $254.65\text{N}\cdot \text{m}$.

The torsion formula for allowable maximum shear stress in the solid shaft $\left({\tau }_{\text{allow}}\right)$ is shown below:

${\tau }_{\text{allow}}=\frac{T_{BC}c}{J}$ (5)

Here, $T_{BC}$ is the maximum torque in the segment BC, J is the polar moment of inertia, and c is the outer radius of the shaft.

The outer radius of the shaft is r.

The polar moment of inertia for a solid shaft of radius $\left(r\right)$ is $\frac{\pi }{2}{r}^4$.

Substitute r for c and $\frac{\pi }{2}{r}^4$ for J in Equation (5).

$\begin{array}{c}{\tau }_{\text{allow}}=\frac{T_{BC}r}{\frac{\pi }{2}{r}^4}\\ =\frac{2T_{BC}}{\pi r^3}\end{array}$ (6)

Substitute 75 MPa for ${\tau }_{\text{allow}}$ and $254.65\text{N}\cdot \text{m}$ for $T_{BC}$ in Equation (6).

$\begin{array}{l}75\text{MPa}=\frac{2\left(254.65\text{N}\cdot \text{m}\right)}{\pi {\left(30\text{mm}\right)}^3}\\ 75\frac{\text{N}}{{\text{mm}}^{\text{2}}}=\frac{2\left(254.65\text{N}\cdot \text{m}\times \frac{{10}^3\text{mm}}{1\text{m}}\right)}{\pi {\left(r\right)}^3}\\ r^3=2,161.4515\\ r=13\text{mm}\end{array}$

The diameter of the shaft is twice the radius of the shaft. So the value of diameter is 26 mm.

Therefore, the required minimum diameter of the shaft is $\underset{\_}{26\text{mm}}$.

Determine the angle of twist $\left(\varphi \right)$ of the shaft using the relation:

$\varphi =\frac{TL}{JG}$ (7)

Here, L is the length of the shaft and G is the shear modulus of elasticity of the material.

Rearrange Equation (7) for angle of twist of gear A relative to gear C $\left({\varphi }_{A/C}\right)$.

$\begin{array}{c}{\varphi }_{A/C}={\displaystyle \sum \frac{TL}{JG}}\\ =\frac{\left(T_{AB}{L}_{AB}+T_{BC}{L}_{BC}\right)}{JG}\end{array}$ (8)

Refer the properties of A992 steel.

The value of shear modulus of elasticity of A992 steel is 75 GPa.

The value of radius of the solid shaft is 13 mm.

Substitute $\frac{\pi }{2}{r}^4$ for J in Equation (8).

$\begin{array}{c}{\varphi }_{A/C}=\frac{\left(T_{AB}{L}_{AB}+T_{BC}{L}_{BC}\right)}{\left(\frac{\pi }{2}{r}^4\right)G}\\ =\frac{2\left(T_{AB}{L}_{AB}+T_{BC}{L}_{BC}\right)}{\left(\pi r^4\right)G}\end{array}$ (9)

Refer Figure 2.

The torque in the region AB of the shaft is $T_{AB}=159.15\text{N}\cdot \text{m}$.

Refer Figure 1.

The torque in the region BC of the shaft is $T_{BC}=254.65\text{N}\cdot \text{m}$.

Substitute $159.15\text{N}\cdot \text{m}$ for $T_{AB}$, 300 mm for $L_{AB}$, $254.65\text{N}\cdot \text{m}$ for $T_{BC}$, 300 mm for $L_{BC}$, 13 mm for $r$, and 75 GPa for $G$ in Equation (9).

$\begin{array}{c}{\varphi }_{A/C}=\frac{2\left(\left(159.15\text{N}\cdot \text{m}\right)\left(300\text{mm}\right)+\left(254.65\text{N}\cdot \text{m}\right)\left(300\text{mm}\right)\right)}{\left(\pi {\left(13\text{mm}\right)}^4\right)\left(75\text{GPa}\right)}\\ =\frac{2\left(\left(159.15\text{N}\cdot \text{m}\right)\left(300\text{mm}\times \frac{{10}^{-3}\text{m}}{1\text{mm}}\right)+\left(254.65\text{N}\cdot \text{m}\right)\left(300\text{mm}\times \frac{{10}^{-3}\text{m}}{1\text{mm}}\right)\right)}{\left(\pi {\left(13\text{mm}\times \frac{{10}^{-3}\text{m}}{1\text{mm}}\right)}^4\right)\left(75\text{GPa}\times \frac{{10}^9\frac{\text{N}}{{\text{m}}^{\text{2}}}}{1\text{GPa}}\right)}\\ =0.03689\text{rad}\\ =0.03689\text{rad}\left(\frac{180°}{\pi \text{rad}}\right)\end{array}$

$=2.11°$

Therefore, the angle of twist of gear A relative to gear C is $\underset{\_}{2.11°}$.