Chapter 5, Problem 4PA

1.

To determine

Construct a cost-volume-profit chart indicating the break-even sales for last year, and verify the answer using the break-even equation.

Explanation of Solution

Cost-Volume-Profit Analysis: It is a method followed to analyze the relationship between the sales, costs, and the related profit or loss at various levels of units sold. In other words, it shows the effect of the changes in the cost and the sales volume on the operating income of the company.

Construct a cost-volume-profit chart indicating the break-even sales for last year.

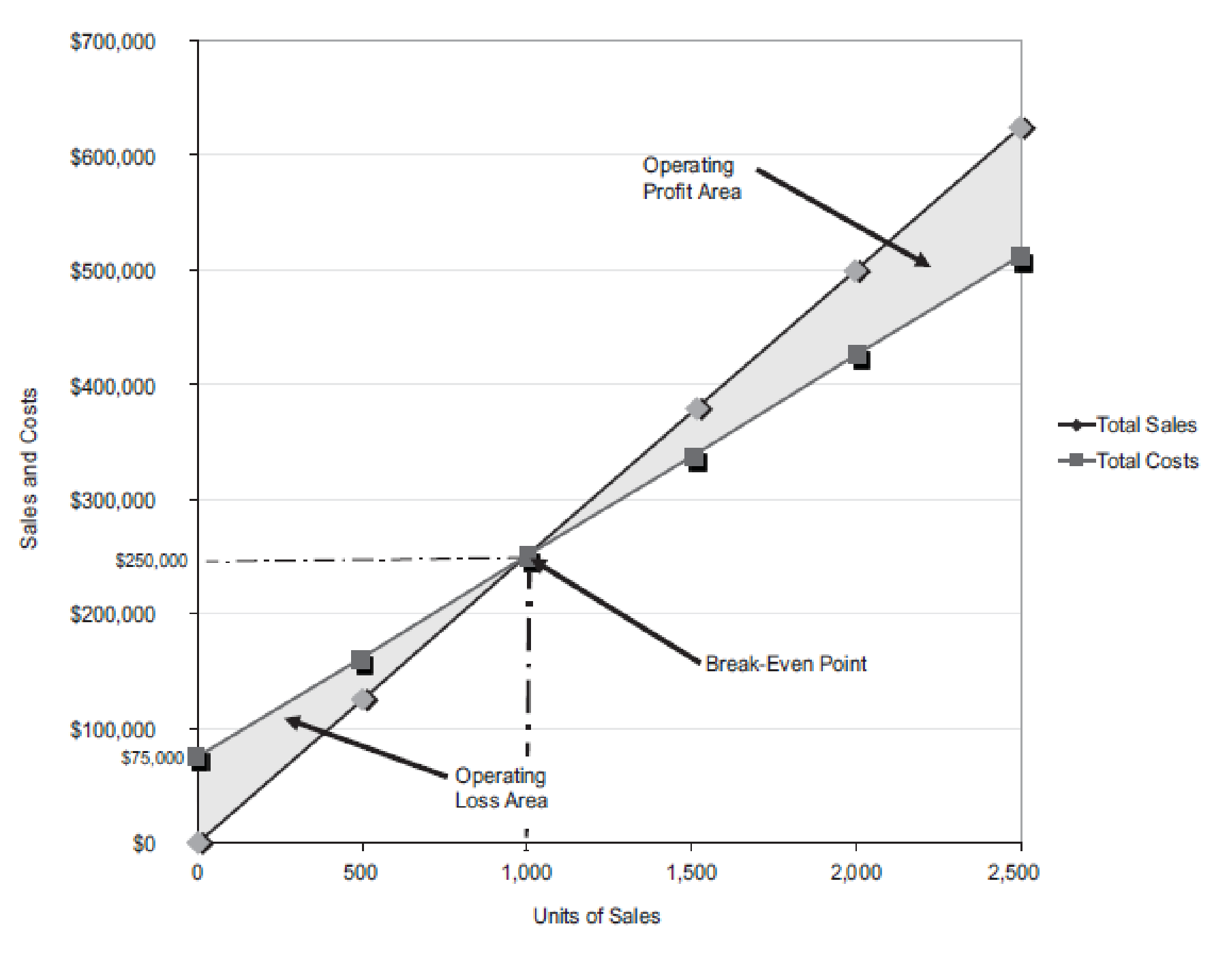
Figure (1)

The volume in units of sales is shown on the horizontal axis. The maximum relevant range is 2,500 units. The sales and the total costs (fixed cost and variable cost) in dollars is shown on the vertical axis. The maximum relevant range of sales and total costs is $700,000.

The total sales line is drawn right upward by connecting the first point at $0 to the second point at $625,000$\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$ for 2,500 units sold (maximum relevant range on the horizontal axis).

The total cost line is drawn right upward by connecting the first point at $75,000 (fixed cost) on the vertical axis to the second point at $512,500$\left[\$75,000+\text{\$437,500}\right]$ at the end of the relevant range. The variable cost is $\$437,500\left(\text{2,500}\text{units×\$175}\text{per}\text{unit}\right)$.

The break-even point is the intersection point where the total sales line and total cost line meet. The vertical dotted line drawn downward from the intersection point reaches at 1,000 units. It indicates the break-even sales (units). The horizontal line drawn to the left towards the vertical axis reaches at $250,000. It indicates the break-even sales (dollars).

The operating profit area is the area where the total sales line exceeds the total cost line. However, the operating loss area is the area where the total cost exceeds the total sales line.

Verify the answer using the break-even equation as follows:

Determine the break-even sales in units.

Fixed cost =$75,000

Contribution margin per unit =$75 per unit (1)

$\begin{array}{c}\text{Break-even}\text{point}\text{in}\text{Sales}\left(\text{units}\right)=\frac{\text{Fixed}\text{Costs}}{\text{Contribution}\text{Margin}\text{per}\text{unit}}\\ =\frac{\$75,000}{\$75}\\ =1,000\text{units}\end{array}$

Determine the break-even sales in dollars.

Fixed cost =$75,000

Contribution margin ratio =30% (2)

$\begin{array}{c}\text{Break-even}\text{point}\text{in}\text{Sales}\left(\text{Dollars}\right)=\frac{\text{Fixed}\text{Costs}}{\text{Contribution}\text{Margin}\text{ratio}}\\ =\frac{\$75,000}{30\%}\\ =\$75,000\times \frac{100}{30}\\ =\$250,000\end{array}$

Working note (1):

Compute the contribution margin per unit.

Selling price per unit =$250 per unit

Variable cost per unit =$175 per unit

$\begin{array}{c}\text{Contribution}\text{Margin}\text{per}\text{unit}\text{=}\left(\begin{array}{l}\text{Selling}\text{price}\\ \text{per}\text{unit}\end{array}\right)-\left(\begin{array}{l}\text{Variable}\text{cost}\\ \text{per}\text{unit}\end{array}\right)\\ \text{=\$250}\text{per}\text{unit}-\text{\$175}\text{per}\text{unit}\\ \text{=\$75}\text{per}\text{unit}\end{array}$

Working note (2):

Determine the contribution margin ratio.

Contribution margin =$75 per unit (1)

Selling price per unit =$250 per unit

$\begin{array}{c}\text{Contribution}\text{Margin}\text{Ratio }=\frac{\text{Contribution}\text{Margin}}{\text{Sales}}\times 100\\ =\frac{\$75perunit}{\$250perunit}\times 100\\ =30\%\end{array}$

2(A)

To determine

Compute the income from operations for last year.

Explanation of Solution

Compute the income from operations for last year as follows:

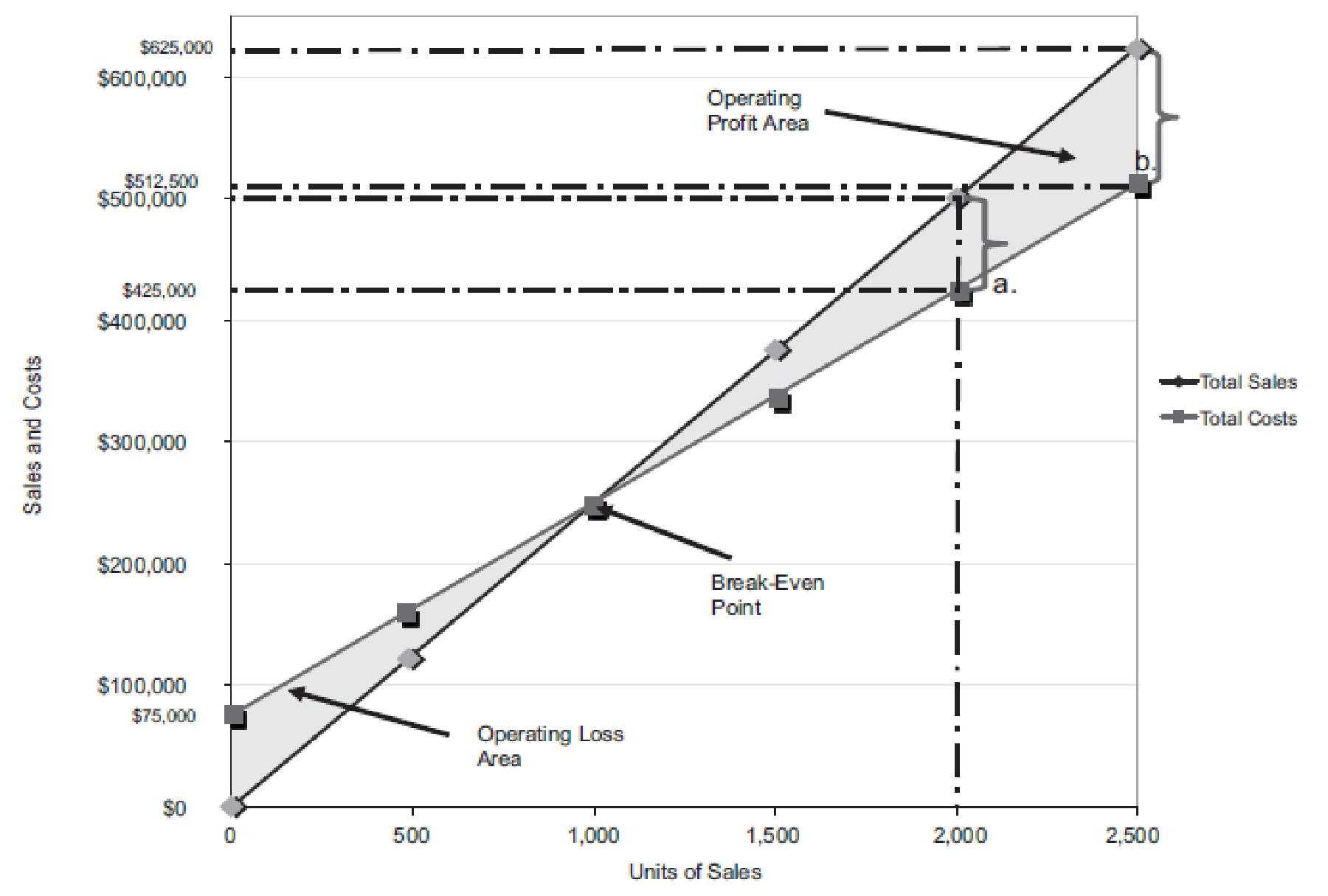
Figure (2)

Last year, the number of units sold is 2,000 units (3). The total sales is $500,000. The total cost is $\$425,000\left[\$75,000+\text{\$350,000}\right]$ for 2,000 units sold. The fixed cost is $75,000. The variable cost is $\$350,000\left(\text{2,000}\text{units×\$175}\text{per}\text{unit}\right)$. A dotted line is drawn from the total sales at $500,000 on the vertical axis towards the right and a dotted line is drawn upward for the 2,000 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of sales at 2,000 units.

Similarly, a dotted line is drawn from the total cost at $425,000 on the vertical axis towards the right and a dotted line is drawn upward for the 2,000 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of total cost at 2,000 units.

The dotted line from sales is above the dotted line for total cost. This indicates the income from operations. Thus, the area in between the two dotted lines is the income from operations of $\$75,000\left(\$500,000-\$425,000\right)$.

Verify the answers using the mathematical approach to cost-volume-profit analysis.

Determine the income from operations for the last year.

Determine the income from operations for 2,000 units
Particulars	Amount ($)	Amount ($)
Sales		500,000
Less: Fixed costs	75,000
Variable costs $\left[\text{2,000}\text{units}\left(3\right)\text{×\$175}\text{per}\text{unit}\right]$	350,000	(425,000)
Income from operations		75,000

Table (1)

Working note (3):

Determine the number of units sold.

Sales =$500,000

Selling price per unit =$250 per unit

$\begin{array}{c}\left(\begin{array}{l}\text{Number}\text{of}\text{units}\\ \text{sold}\end{array}\right)=\frac{\text{Sales}}{\left(\begin{array}{l}\text{Selling}\text{price}\\ \text{per}\text{unit}\end{array}\right)}\\ =\frac{\$500,000}{\text{\$250}\text{per}\text{unit}}\\ =2,000\text{units}\end{array}$

2(B)

To determine

Compute the maximum income from operations realized during the year.

Explanation of Solution

The maximum relevant range for number of units to be sold is 2,500 units. Thus, the total sale is $\$625,000\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$. The total cost is $\$512,500\left[\$75,000+\text{\$437,500}\right]$ for 2,500 units sold. The fixed cost is $75,000. The variable cost is $\$437,500\left(\text{2,500}\text{units×\$175}\text{per}\text{unit}\right)$. A dotted line is drawn from the total sales at $625,000 on the vertical axis towards the right and a dotted line is drawn upward for the 2,500 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of sales at 2,500 units.

Similarly, a dotted line is drawn from the total cost at $512,500 on the vertical axis towards the right and a dotted line is drawn upward for the 2,500 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of total cost at 2,500 units.

The dotted line from sales is above the dotted line for total cost. This indicates the income from operations. Thus, the area in between the two dotted lines is the income from operations of $\$112,500\left(\$625,000-\$512,500\right)$.

Determine the maximum income from operations that could have been realized during the year.

Determine the income from operations for 2,500 units
Particulars	Amount ($)	Amount ($)
Sales $\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$		625,000
Less: Fixed costs	75,000
Variable costs $\left[\text{2,500}\text{units×\$175}\text{per}\text{unit}\right]$	437,500	(512,500)
Income from operations		112,500

Table (2)

3.

To determine

Construct a cost-volume-profit chart indicating the break-even sales for the current year, and verify the answer using the break-even equation.

Explanation of Solution

Construct a cost-volume-profit chart indicating the break-even sales for the current year as follows:

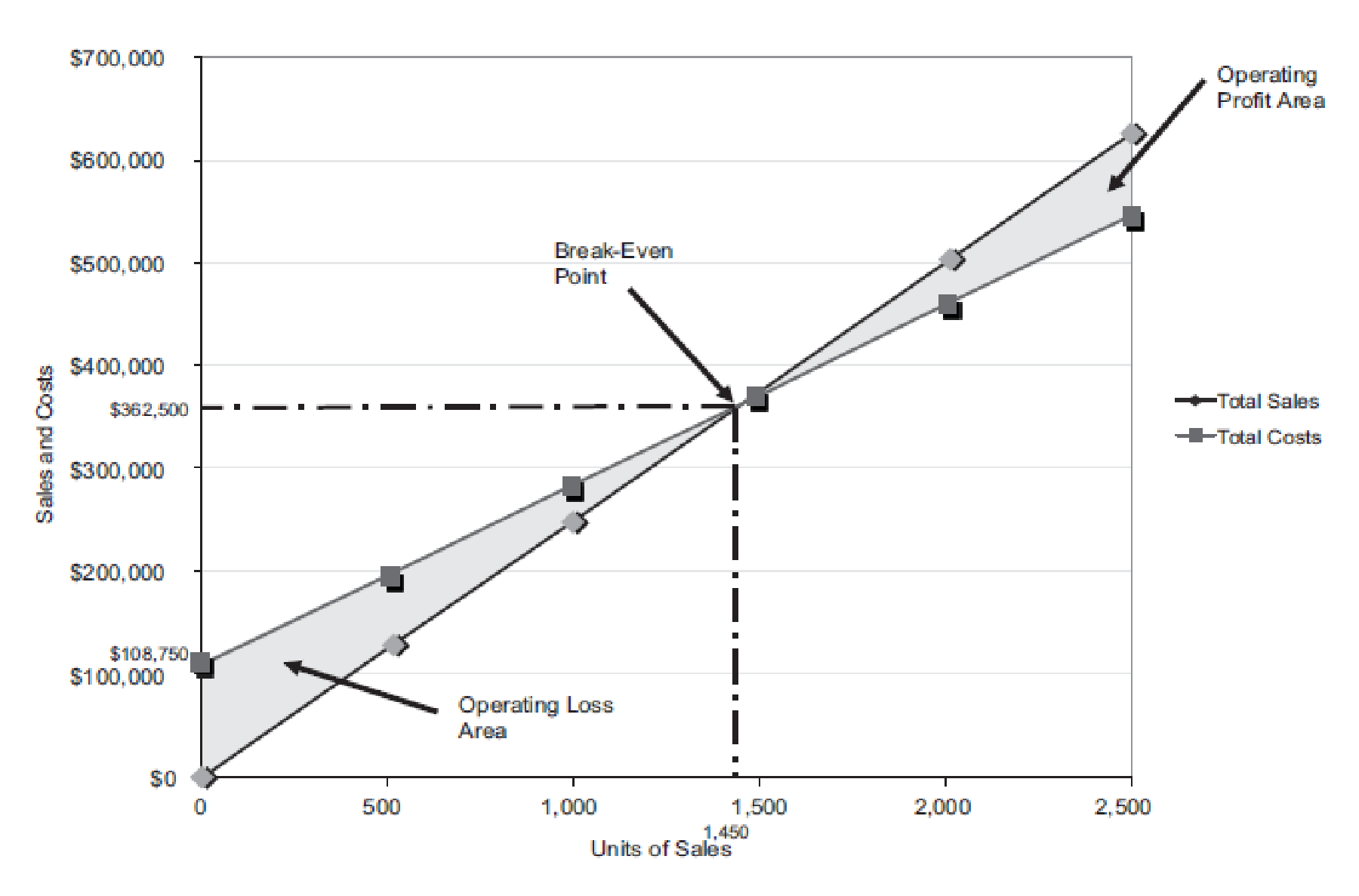
Figure (3)

The volume in units of sales is shown on the horizontal axis. The maximum relevant range is 2,500 units. The sales and the total costs (fixed cost and variable cost) in dollars is shown on the vertical axis. The maximum relevant range of sales and total costs is $700,000.

The total sales line is drawn right upward by connecting the first point at $0 to the second point at $625,000$\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$ for 2,500 units sold (maximum relevant range on the horizontal axis).

The total cost line is drawn right upward by connecting the first point at $\$108,750\left[\$75,000+\text{\$33,750}\right]$ (total fixed cost) on the vertical axis to the second point at $546,250$\left[\$108,750+\text{\$437,500}\right]$ at the end of the relevant range. The variable cost is $\$437,500\left(\text{2,500}\text{units×\$175}\text{per}\text{unit}\right)$.

The break-even point is the intersection point where the total sales line and total cost line meet. The vertical dotted line drawn downward from the intersection point reaches at 1,450 units. It indicates the break-even sales (units). The horizontal line drawn to the left towards the vertical axis reaches at $362,500. It indicates the break-even sales (dollars).

The operating profit area is the area where the total sales line exceeds the total cost line. However, the operating loss area is the area where the total cost exceeds the total sales line.

Verify the answer using the break-even equation as follows:

Determine the break-even sales in units.

Fixed cost =$75,000

Increase in fixed cost (billboard advertising) =$33,750

Contribution margin per unit =$75 per unit (1)

$\begin{array}{c}\text{Break-even}\text{point}\text{in}\text{Sales}\left(\text{units}\right)=\frac{\text{Total}\text{Fixed}\text{Costs}}{\text{Contribution}\text{Margin}\text{per}\text{unit}}\\ =\frac{\$75,000+\$33,750}{\$75}\\ =\frac{\$108,750}{\$75}\\ =1,450\text{units}\end{array}$

Determine the break-even sales in dollars.

Fixed cost =$75,000

Increase in fixed cost (billboard advertising) =$33,750

Contribution margin ratio =30% (2)

$\begin{array}{c}\text{Break-even}\text{point}\text{in}\text{Sales}\left(\text{Dollars}\right)=\frac{\text{Total}\text{Fixed}\text{Costs}}{\text{Contribution}\text{Margin}\text{ratio}}\\ =\frac{\$75,000+\$33,750}{30\%}\\ =\frac{\$108,750}{30\%}\\ =\$108,750\times \frac{100}{30}\\ =\$362,500\end{array}$

4(A)

To determine

Compute the income from operations for sales 2,000 units, and verify the answers using the mathematical approach to cost-volume-profit analysis

Explanation of Solution

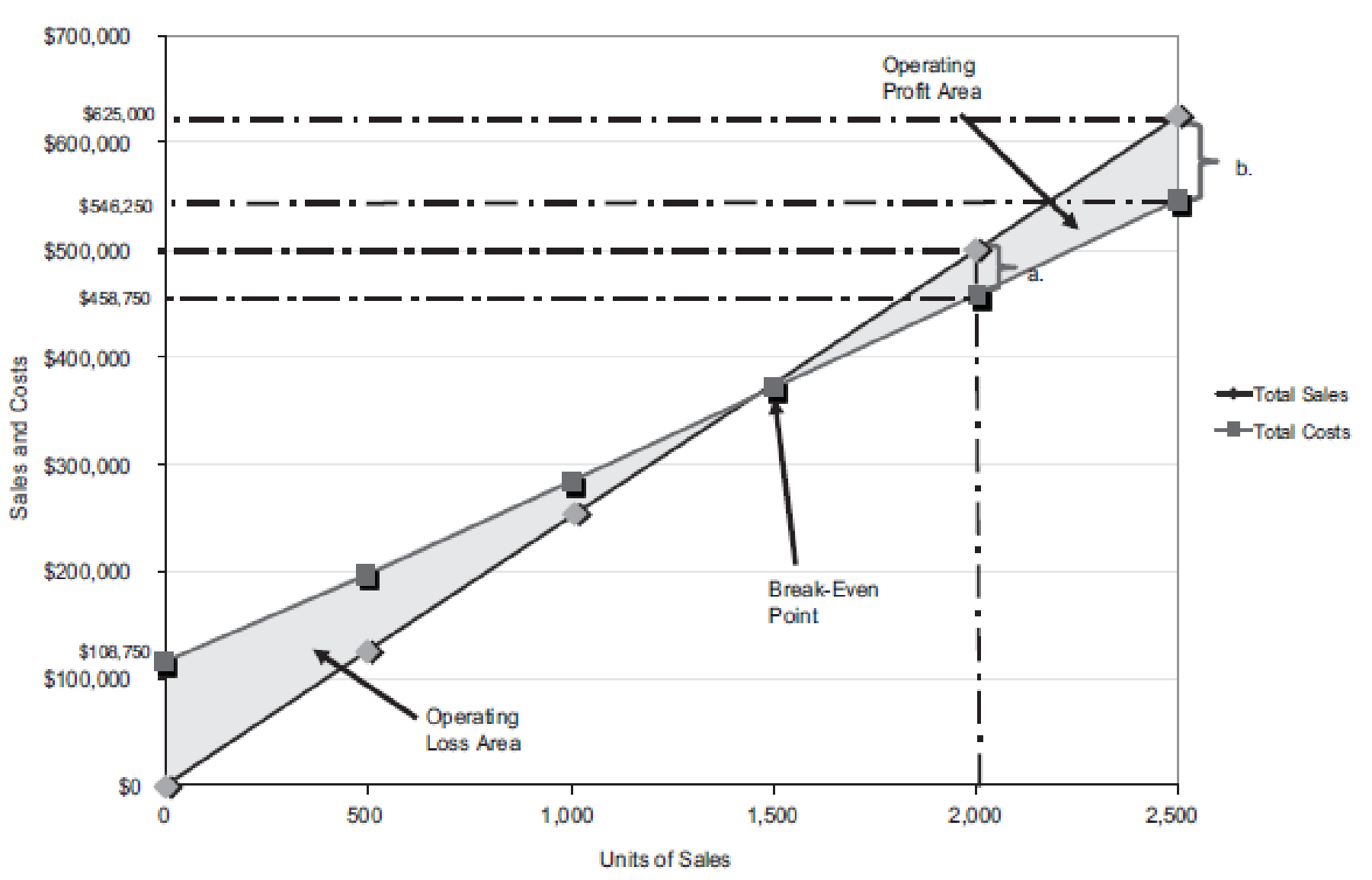
Figure (4)

Last year, the number of units sold is 2,000 units (3). The total sales is $500,000. The total cost is $\$458,750\left[\$108,750+\text{\$350,000}\right]$ for 2,000 units sold. The total fixed cost is $\$108,750\left[\$75,000+\text{\$33,750}\right]$. The variable cost is $\$350,000\left(\text{2,000}\text{units×\$175}\text{per}\text{unit}\right)$. A dotted line is drawn from the total sales at $500,000 on the vertical axis towards the right and a dotted line is drawn upward for the 2,000 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of sales at 2,000 units.

Similarly, a dotted line is drawn from the total cost at $458,750 on the vertical axis towards the right and a dotted line is drawn upward for the 2,000 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of total cost at 2,000 units.

The dotted line from sales is above the dotted line for total cost. This indicates the income from operations. Thus, the area in between the two dotted lines is the income from operations of $\$41,250\left(\$500,000-\$458,750\right)$.

Verify the answers using the mathematical approach to cost-volume-profit analysis.

Determine the income from operations for the last year.

Determine the income from operations for 2,000 units
Particulars	Amount ($)	Amount ($)
Sales		500,000
Less: Total Fixed costs $\left[\$75,000+\$33,750\right]$	108,750
Variable costs $\left[\text{2,000}\text{units}\left(3\right)\text{×\$175}\text{per}\text{unit}\right]$	350,000	(458,750)
Income from operations		41,250

Table (3)

4(B)

To determine

Compute the maximum income from operations that could have been realized during the year and verify the answer.

Explanation of Solution

The maximum relevant range for number of units to be sold is 2,500 units. Thus, the total sales is $\$625,000\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$. The total cost is $\$546,250\left[\$108,750+\text{\$437,500}\right]$ for 2,500 units sold. The total fixed cost is $\$108,750\left[\$75,000+\text{\$33,750}\right]$. The variable cost is $\$437,500\left(\text{2,500}\text{units×\$175}\text{per}\text{unit}\right)$. A dotted line is drawn from the total sales at $625,000 on the vertical axis towards the right and a dotted line is drawn upward for the 2,500 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of sales at 2,500 units.

Similarly, a dotted line is drawn from the total cost at $546,250 on the vertical axis towards the right and a dotted line is drawn upward for the 2,500 units sold from the horizontal axis. The two dotted line meet at a point which indicates the point of total cost at 2,500 units.

The dotted line from sales is above the dotted line for total cost. This indicates the income from operations. Thus, the area in between the two dotted lines is the income from operations of $\$78,750\left(\$625,000-\$546,250\right)$.

Verification:

Determine the income from operations for 2,500 units
Particulars	Amount ($)	Amount ($)
Sales $\left[\text{2,500}\text{units×\$250}\text{per}\text{unit}\right]$		625,000
Less: Total Fixed costs $\left[\$75,000+\$33,750\right]$	108,750
Variable costs $\left[\text{2,500}\text{units×\$175}\text{per}\text{unit}\right]$	437,500	(546,250)
Income from operations		78,750

Table (4)