
Practical Management Science, Loose-leaf Version
5th Edition
ISBN: 9781305631540
Author: WINSTON, Wayne L.; Albright, S. Christian
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 5, Problem 42P
Summary Introduction
To determine: The way to minimize the total distance.
Introduction: In linear programming, the unbounded solution would occur when the objective function is infinite. If no solution satisfied the constraints, then it is said to be an unfeasible solution.
Expert Solution & Answer
Explanation of Solution
Determine the number of students in districts from each community:
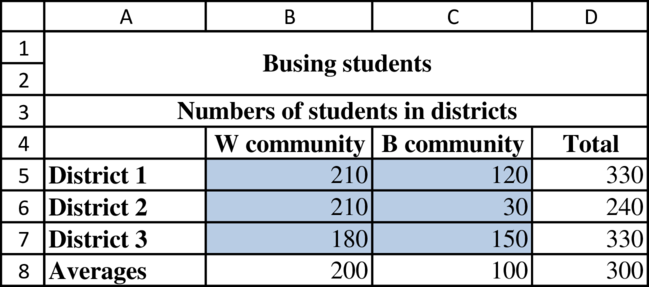
Determine the busing distance:
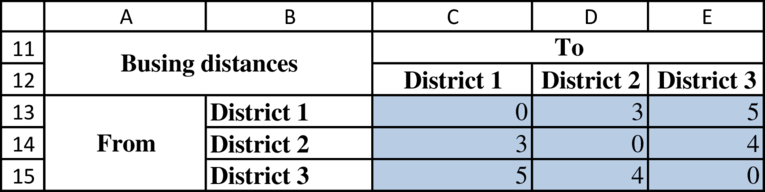
Determine the number of students on the bus from each community:
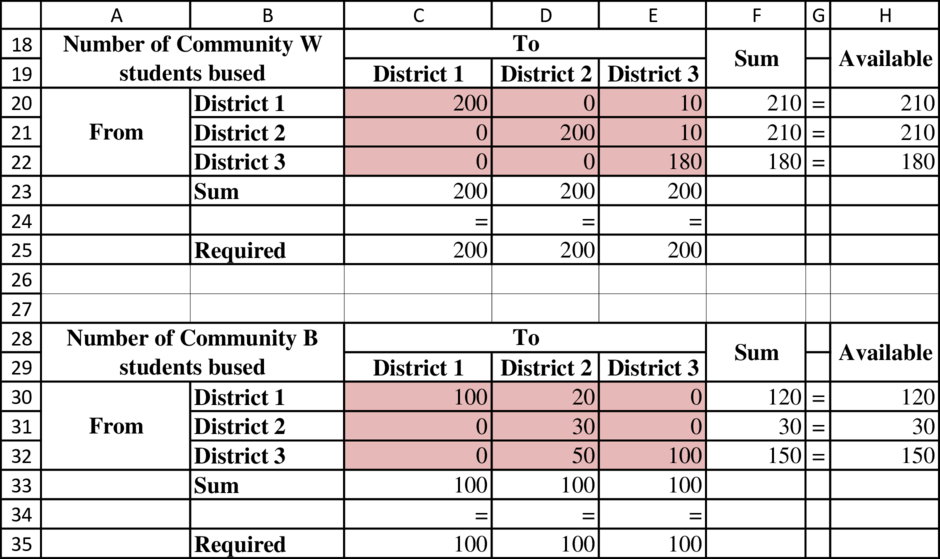
Determine the busing distances:


Formula to determine the number of students in districts from each community:
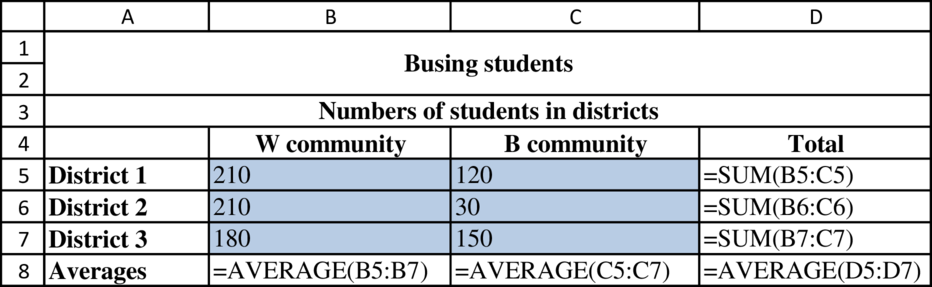
Formulae to determine the number of students in the bus from each community:
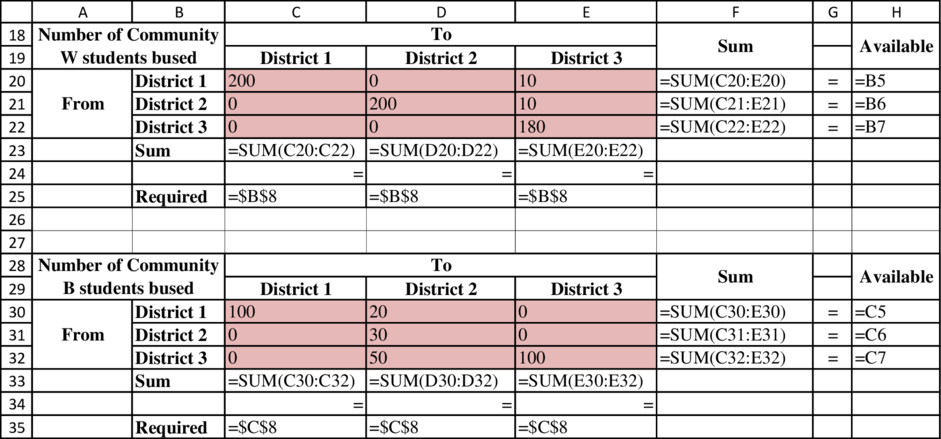
Formula to determine the busing distances:

Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
In the 2016 "ATB: digital disruption in the parking meter industry"
1. Identification + use of suitable decision criteriato rank options▪ Development of practical options in relation toidentified issue(s) + prior analysis▪ Qualitative + financial evaluation andcomparison of options 2
2.
Detailed + practical action to putrecommendations in place (both short & long-run)▪ Timeline of sequence of actions, e.g. Ganttchart▪ Controls + timeline to measure if plan is ontrack▪ Contingency plan
In the 2016, "ATB: digital disruption in the parking meter industry" case provide a financial analysis of firm
Several disadvantages are associated with lying in negotiation which include all of the following except _____.
Group of answer choices
the liar can be caught and face criminal charges
increased risk of a bidding war
cultural cost in terms of people being suspicious about others within the organization
personal reputation and trustworthiness is damaged
Chapter 5 Solutions
Practical Management Science, Loose-leaf Version
Ch. 5.2 - Prob. 1PCh. 5.2 - Prob. 2PCh. 5.2 - Prob. 3PCh. 5.2 - Prob. 4PCh. 5.2 - Prob. 5PCh. 5.2 - Prob. 6PCh. 5.2 - Prob. 7PCh. 5.2 - Prob. 8PCh. 5.2 - Prob. 9PCh. 5.3 - Prob. 10P
Ch. 5.3 - Prob. 11PCh. 5.3 - Prob. 12PCh. 5.3 - Prob. 13PCh. 5.3 - Prob. 14PCh. 5.3 - Prob. 15PCh. 5.3 - Prob. 16PCh. 5.3 - Prob. 17PCh. 5.3 - Prob. 18PCh. 5.4 - Prob. 19PCh. 5.4 - Prob. 20PCh. 5.4 - Prob. 21PCh. 5.4 - Prob. 22PCh. 5.4 - Prob. 23PCh. 5.4 - Prob. 24PCh. 5.4 - Prob. 25PCh. 5.4 - Prob. 26PCh. 5.4 - Prob. 27PCh. 5.4 - Prob. 28PCh. 5.4 - Prob. 29PCh. 5.5 - Prob. 30PCh. 5.5 - Prob. 31PCh. 5.5 - Prob. 32PCh. 5.5 - Prob. 33PCh. 5.5 - Prob. 34PCh. 5.5 - Prob. 35PCh. 5.5 - Prob. 36PCh. 5.5 - Prob. 37PCh. 5.5 - Prob. 38PCh. 5 - Prob. 42PCh. 5 - Prob. 43PCh. 5 - Prob. 44PCh. 5 - Prob. 45PCh. 5 - Prob. 46PCh. 5 - Prob. 47PCh. 5 - Prob. 48PCh. 5 - Prob. 49PCh. 5 - Prob. 50PCh. 5 - Prob. 51PCh. 5 - Prob. 52PCh. 5 - Prob. 53PCh. 5 - Prob. 54PCh. 5 - Prob. 55PCh. 5 - Prob. 56PCh. 5 - Prob. 57PCh. 5 - Prob. 58PCh. 5 - Prob. 59PCh. 5 - Prob. 60PCh. 5 - Prob. 61PCh. 5 - Prob. 62PCh. 5 - Prob. 63PCh. 5 - Prob. 64PCh. 5 - Prob. 65PCh. 5 - Prob. 66PCh. 5 - Prob. 67PCh. 5 - Prob. 68PCh. 5 - Prob. 69PCh. 5 - Prob. 70PCh. 5 - Prob. 71PCh. 5 - Prob. 72PCh. 5 - Prob. 73PCh. 5 - Prob. 74PCh. 5 - Prob. 75PCh. 5 - Prob. 76PCh. 5 - Prob. 77PCh. 5 - Prob. 80PCh. 5 - Prob. 81PCh. 5 - Prob. 82PCh. 5 - Prob. 83PCh. 5 - Prob. 85PCh. 5 - Prob. 86PCh. 5 - Prob. 87PCh. 5 - Prob. 2C
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, operations-management and related others by exploring similar questions and additional content below.Similar questions
- A major obstacle to reaching integrative negotiation agreements is negotiators' beliefs about the outcome of some future event. A _____ is a type of agreement in which parties leverage differences of opinion to form an integrative agreement. Group of answer choices compromise contract fixed contract speculative agreement contingent contractarrow_forwardHow can trust be measured? Many surveys are available that measure trust based on behavioral and interpersonal traits. Find a measuring tool for trust and list the following. What is the tool (be sure to use APA guidelines when citing the author and list the complete reference at the end of the post)? How does the tool measure trust? Could the tool provide an accuracy of truth? Why did you select this particular tool?arrow_forwardRespond to Adam; Agree or disagree The Trust Scale is perhaps the most famous tool for measuring trust, which was made by Mayer, Davis, and Schoorman (1995). It is based on the person's ability (competence), benevolence (intentions), and integrity (following principles). This tool is an assessment of other people's perceptions about their tests (competence), their beliefs (intentions), and their rules (integrity). A Likert-type scale questionnaire uses it; participants express their opinions on the above, and then data are summed in order to find out the general level of trust in the relationship. In organizational settings, where it is broadly used for measuring employee trust in leadership or peers, it also gives useful insights into workplace dynamics as well as potential barriers to collaboration (Mayer, Davis, & Schoorman, 1995). This tool is likely to render a true measurement of trust, especially in situations that are clearly structured so that trust behaviors are visible…arrow_forward
- Respond to Lisa; Agree or disagree Trust is an essential trait required for relationships to thrive among individuals and even organizations. Employees are also expected to be trustworthy as a core value for building a robust and reliable corporate culture. Even though trust is a vital ingredient for human relationship and helps to understand organizational behaviors and interpersonal relationships, it is challenging measure the trust and its level (Evans & Revelle, 2008). However, several tools have been developed in an attempt to quantify trust but there is no known effectiveness in assessing its level based on interpersonal traits. Many studies have been conducted seeking to know how trust can be measured although they treated trust as situational construct. Some of the tools used include psychometric properties of a new trust inventory known as PTS (Propensity to Trust Survey) and Trust Style Inventory (TSI). PTS mostly relied on online survey data but has been increasingly…arrow_forward◄ Mail 18:09 5G CSTUDY_Jan25_BCOMHO...al_20241129091837.pdf.pdf FORMATIVE ASSESSMENT 1 Read the case study below and answer ALL of the questions that follow. Title: Upskilling and reskilling priorities for the gen Al era [100 MARKS] To realize the opportunity of generative Al, organizations should take a cross-collaborative, scaled approach to upskilling and reskilling workforces. The proliferation of generative artificial intelligence (gen Al) innovations necessitates a new approach to employee attraction, engagement, and retention. Our survey finds that compared to late adopters, companies adopting gen Al earlier place greater emphasis on talent development, with two-thirds already having a strategic approach to address their future talent and skill requirements. Organizations should think about a breadth of gen Al capability needs-from broad fluency supporting business goals, to deep technical and domain-specific capabilities-as well as the speed and scale at which they should be…arrow_forwardQuestion 1 (25 Marks) Procurement is a key strategic function that directly impacts an organisation’s ability to create value, manage risks, and maintain a competitive advantage in the market. Critically analyse the strategic roles of procurement and how procurement practices in the fashion industry can strategically address complex challenges such as supply chain efficiency, sustainability, cost management, and global sourcing. Provide examples from the fashion industry to further your analysis. Question 2 (25 Marks) There are several enablers that need to be in place for a procurement and supply management function to implement a value-generating mode. Examine the extent of these enablers as they present themselves in the fashion industry. Question 3 (25 Marks) You are hired by local clothing chain Fashion World. The brand wants to instill a culture of professional purchasing. Construct a policy document which you would present at the next strategy meeting which inculcates the…arrow_forward
- ◄ Files 18:11 5G CSTUDY_Jan25_SCMH_PS...Final_20241203151014.pdf FORMATIVE ASSESSMENT 1 Read the article below and answer ALL questions that follow Are your favourite fashion brands using forced labour? [100 MARKS] The global fashion and retail industry's reliance on producing quick-tumaround goods at a low cost through outsourcing and complex, globalised supply chains has allowed forced labour to thrive, workers' rights advocates war, claiming that major fashion brands profiting from the model seem reluctant to change. The apparel sector employs over 60 million workers worldwide, according to the World Bank Group. And while 97 percent of fashion and retail brands have codes of conduct and corporate social responsibility (CSR) standards, such policies are neither effective in preventing forced labour nor in ensuring remedy outcomes for workers, according to advocacy group KnowThe Chain KnowTheChain's 2021 Apparel and Footwear Benchmark Report (PDF) recently ranked 37 of the world's…arrow_forwardWhat does a Balanced Workout plan ensure comprehensive fitness? What are the obstacles involved in a Balanced Workout plan to ensure comprehensive Fitness? How does mental well-being entail implementing techniques such as mindfulness, therapy, physical activity, and social support to cultivate emotional resilience and mitigate stress?arrow_forwardIdentify the ethical principles that apply to the case. Include in your discussion how each of the principles of ethical decision making as discussed in the “Underlying Principles of Ethical Patient Care” chapter factored into your decision (beneficence, non-maleficence, autonomy, respect for dignity, veracity, and justice).arrow_forward
- What should I do? Generate Potential Actions. Include choices that cannot be justified. What justifies my choice? Decide on proper ethical action and generate responses to those with opposing arguments (Justification for your choice)arrow_forwardin the 2016 "ATB: Digital Disruption in the parking meter industry" case what recommendations would you give to adress the key issues outlined in the case?arrow_forward1) JIT McDonald’s Style (https://media.gaspar.mheducation.com/GASPARPlayer/play.html?id=46KGfedfilYlJzWH4XxxbLS) What challenges did McDonald’s face with its current operating system? 2. What are the five criteria that McDonald’s new “Made for You” operating system had to meet? 3. Describe how the “Made for You” operating system works.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,