
Concept explainers
(a)
The sketch of the real part of the matter wave pulse shape
(a)
Answer to Problem 35P
The real part of the matter wave pulse shape

Explanation of Solution
Write the expression for the matter wave pulse shape.
Here,
Write the expression for
Here,
Put the above equation in equation (I).
Simplify the above equation.
Take
Take the derivative of
Put the above two equations in equation (II).
Write the real part of
Here,
The plot of
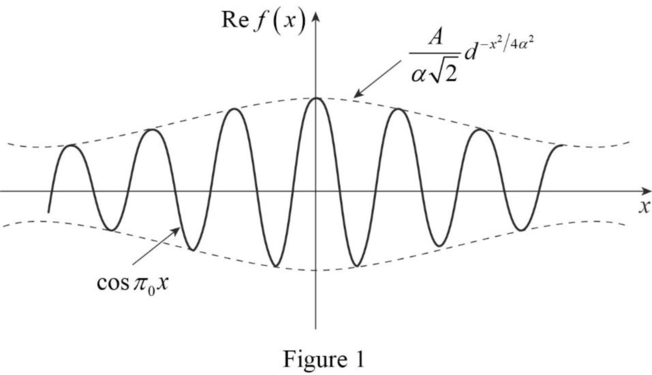
Conclusion:
Therefore, the real part of the matter wave pulse shape
(b)
To show that the width of the matter wave pulse is
(b)
Answer to Problem 35P
It is showed that width of the matter wave pulse is
Explanation of Solution
Write the standard form of the Gaussian function with width
Comparison of equation (III) with the above expression shows that
Conclusion:
Therefore, it is showed that width of the matter wave pulse is
(c)
The width
(c)
Answer to Problem 35P
The width
Explanation of Solution
Compare equations (III) and (IV) to write the expression for
Rewrite the above equation for
Use equations (V) and (VI) to find the value of
Conclusion:
Thus, the width
Want to see more full solutions like this?
Chapter 5 Solutions
Modern Physics
- A bridge truss extends x = 217 m across a river (shown in the figure below) where 0 = 40°. The structure is free to slide horizontally to permit thermal expansion. The structural components are connected by pin joints, and the masses of the bars are small compared with the mass of a 1300 kg car at the center. Calculate the force of tension or compression in each structural component (in N). B D T T T T T 22820 AB AC BC ||| || || || BD N ---Select--- N ---Select--- N ---Select--- N ---Select--- DE N ---Select--- T DC= N ---Select--- TEC N ---Select--- с ✓ Earrow_forwardno ai pleasearrow_forwardA block of mass m₁ = 1.85 kg and a block of mass m₂ is 0.360 for both blocks. 5.90 kg are connected by a massless string over a pulley in the shape of a solid disk having a mass of M = 10.0 kg. The fixed, wedge-shaped ramp makes an angle of 0 = 30.0° as shown in the figure. The coefficient of kinetic friction m M, R m2 Ꮎ (a) Determine the acceleration of the two blocks. (Enter the magnitude of the acceleration.) m/s2 (b) Determine the tensions in the string on both sides of the pulley. left of the pulley right of the pulley N Narrow_forward
- Consider as a system the Sun with Venus in a circular orbit around it. Find the magnitude of the change in the velocity of the Sun relative to the center of mass of the system during the time Venus completes half an orbit. Assume the mass of the Sun is 5.68 x 1029 kg, the mass of Venus is 4.87 × 1024 kg, its period is 1.94 × 107 s, and the radius of its orbit is 1.08 × 1011 m. Ignore the influence of other celestial objects. m/sarrow_forwardYour physics instructor loves to put on physics magic shows for elementary school children. He is working on a new trick and has asked you, his star physics student, for assistance. The figure below shows the apparatus he is designing. Cup Hinged end - Support stick A small ball rests on a support so that the center of the ball is at the same height as the upper lip of a cup of negligible mass that is attached to a uniform board of length = 1.89 m. When the support stick is snatched away, the ball will fall and the board will rotate around the hinged end. As the board hits the table, your instructor wants the ball to fall into the cup. The larger the angle 0, the more time the elementary school children will have to watch the progress of the trick. But if the angle is too large, the cup may not pull ahead of the ball. For example, in the limiting case of 90°, the board would not fall at all! (a) Your instructor wishes to know the minimum angle 0 (in degrees) at which the support would…arrow_forwardno ai pleasearrow_forward
- = Consider the schematic of the molecule shown, with two hydrogen atoms, H, bonded to an oxygen atom, O. The angle between the two bonds is 106°. If the bond length r 0.106 nm long, locate the center of mass of the molecule. The mass mH of the hydrogen atom is 1.008 u, and the mass mo of the oxygen atom is 15.9999 u. (Use a coordinate system centered in the oxygen atom, with the x-axis to the right and the y-axis upward. Give the coordinates of the center of mass in nm.) XCM YOM = = H 53° 53° nm nm r Harrow_forwardAn approximate model for a ceiling fan consists of a cylindrical disk with four thin rods extending from the disk's center, as in the figure below. The disk has mass 2.60 kg and radius 0.200 m. Each rod has mass 0.850 kg and is 0.700 m long. HINT (a) Find the ceiling fan's moment of inertia about a vertical axis through the disk's center. (Enter your answer in kg • m².) kg. m² (b) Friction exerts a constant torque of magnitude 0.113 N m on the fan as it rotates. Find the magnitude of the constant torque provided by the fan's motor if the fan starts from rest and takes 15.0 s and 17.5 full revolutions to reach its maximum speed. (Enter your answer in N. m.) N.marrow_forwardA uniform, thin rod hangs vertically at rest from a frictionless axle attached to its top end. The rod has a mass of 0.780 kg and a length of 1.54 m. (Assume a coordinate system where the +y-direction is up and the +x-direction is to the right. The rod is free to swing about the axle in the x- y plane.) (a) You take a hammer and strike the bottom end of the rod. At the instant the hammer strikes, the force it applies to the rod is (15.71) N. What is the acceleration (in m/s²) of the rod's center of mass at this instant? (Express your answer in vector form.) m/s² a = (b) What is the horizontal force (in N) that the axle exerts on the rod at this same instant? (Express your answer in vector form.) F = N (c) The rod then returns to hanging at rest. You again strike the rod with the hammer, applying the same force, but now you strike it at its midpoint. What now is the acceleration of the center of mass (in m/s²) at the instant of impact? (Express your answer in vector form.) m/s² a = (d)…arrow_forward
- Find the net torque on the wheel in the figure below about the axle through O perpendicular to the page, taking a = 9.00 cm and b = 23.0 cm. (Indicate the direction with the sign of your answer. Assume that the positive direction is counterclockwise.) N.m 10.0 N 30.0% 12.0 N 9.00 Narrow_forwardAn automobile tire is shown in the figure below. The tire is made of rubber with a uniform density of 1.10 × 103 kg/m³. The tire can be modeled as consisting of two flat sidewalls and a tread region. Each of the sidewalls has an inner radius of 16.5 cm and an outer radius of 30.5 cm as shown, and a uniform thickness of 0.600 cm. The tread region can be approximated as having a uniform thickness of 2.50 cm (that is, its inner radius is 30.5 cm and outer radius is 33.0 cm as shown) and a width of 19.2 cm. What is the moment of inertia (in kg. m²) of the tire about an axis perpendicular to the page through its center? 33.0 cm 16.5 cm Sidewall Ο 30.5 cm Tread i Enter a number. Find the moment of inertia of the sidewall and the moment of inertia of the tread region. Each can be modeled as a cylinder of nonzero thickness. What is the inner and outer radius for each case? What is the formula for the moment of inertia for a thick-walled cylinder? How can you find the mass of a hollow cylinder?…arrow_forwardYou have just bought a new bicycle. On your first riding trip, it seems that the bike comes to rest relatively quickly after you stop pedaling and let the bicycle coast on flat ground. You call the bicycle shop from which you purchased the vehicle and describe the problem. The technician says that they will replace the bearings in the wheels or do whatever else is necessary if you can prove that the frictional torque in the axle of the wheels is worse than -0.02 N . m. At first, you are discouraged by the technical sound of what you have been told and by the absence of any tool to measure torque in your garage. But then you remember that you are taking a physics class! You take your bike into the garage, turn it upside down and start spinning the wheel while you think about how to determine the frictional torque. The driveway outside the garage had a small puddle, so you notice that droplets of water are flying off the edge of one point on the tire tangentially, including drops that…arrow_forward
 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





