
ALGEBRA+TRIGONOMETRY
7th Edition
ISBN: 9780136922179
Author: Blitzer
Publisher: RENT PEARS
expand_more
expand_more
format_list_bulleted
Question
Chapter 5, Problem 31RE
To determine
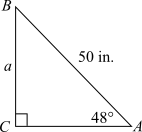
To calculate: The measure of the side of the right
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1.
vector projection.
Assume, ER1001 and you know the following:
||||=4, 7=-0.5.7.
For each of the following, explicitly compute the value.
འབ
(a)
(b)
(c)
(d)
answer.
Explicitly compute ||y7||. Explain your answer.
Explicitly compute the cosine similarity of and y. Explain your
Explicitly compute (x, y). Explain your answer.
Find the projection of onto y and the projection of onto .
2.
Answer the following questions using vectors u and v.
--0-0-0
=
find the the cosine similarity and the angle between u and v.
འརྒྱ
(a)
(b)
find the scalar projection of u onto v.
(c)
find the projection of u onto v.
(d)
(e)
(f)
find the scalar projection of onto u.
find the projection of u onto u.
find the projection of u onto and the projection of onto . (Hint:
find the inner product and verify the orthogonality)
Please type out answer
Chapter 5 Solutions
ALGEBRA+TRIGONOMETRY
Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Prob. 5CVCCh. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Prob. 8CVCCh. 5.1 - Prob. 9CVCCh. 5.1 - Prob. 10CVC
Ch. 5.1 - In Exercises 1-6, the measure of an angle is...Ch. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - In Exercises 1-6, the measure of an angle is...Ch. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - In Exercises 7-12, find the radian measure of the...Ch. 5.1 - Prob. 8ECh. 5.1 - In Exercises 7-12, find the radian measure of the...Ch. 5.1 - Prob. 10ECh. 5.1 - In Exercises 7-12, find the radian measure of the...Ch. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - In Exercises 13-20, convert each angle in degrees...Ch. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - In Exercises 13-20, convert each angle in degrees...Ch. 5.1 - In Exercises 21-28, convert each angle in radians...Ch. 5.1 - In Exercises 21-28, convert each angle in radians...Ch. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - In Exercises 21-28, convert each angle in radians...Ch. 5.1 - In Exercises 21-28, convert each angle in radians...Ch. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - In Exercises 29-34. convert each angle in degrees...Ch. 5.1 - In Exercises 29-34. convert each angle in degrees...Ch. 5.1 - In Exercises 29-34. convert each angle in degrees...Ch. 5.1 - In Exercises 29-34. convert each angle in degrees...Ch. 5.1 - Prob. 33ECh. 5.1 - In Exercises 29-34. convert each angle in degrees...Ch. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - In Exercises 35-40, convert each angle in radians...Ch. 5.1 - In Exercises 35-40, convert each angle in radians...Ch. 5.1 - Prob. 39ECh. 5.1 - In Exercises 35-40, convert each angle in radians...Ch. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - Prob. 48ECh. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - Prob. 50ECh. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - In Exercises 41-56, use the circle shown in the...Ch. 5.1 - Prob. 57ECh. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - Prob. 59ECh. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - In Exercises 57-70, find a positive angle less...Ch. 5.1 - Prob. 68ECh. 5.1 - Prob. 69ECh. 5.1 - Prob. 70ECh. 5.1 - In Exercises 71-74, find the length of the arc on...Ch. 5.1 - In Exercises 71-74, find the length of the arc on...Ch. 5.1 - Prob. 73ECh. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - In Exercises 75-76, express each angular speed in...Ch. 5.1 - Prob. 77ECh. 5.1 - Prob. 78ECh. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.1 - Prob. 82ECh. 5.1 - Prob. 83ECh. 5.1 - In Exercises 83-86. find the absolute value of the...Ch. 5.1 - In Exercises 83-86. find the absolute value of the...Ch. 5.1 - Prob. 86ECh. 5.1 - Prob. 87ECh. 5.1 - Prob. 88ECh. 5.1 - Prob. 89ECh. 5.1 - The minute hand of a clock is 6 inches long and...Ch. 5.1 - The figure shows a highway sign that warns of a...Ch. 5.1 - Prob. 92ECh. 5.1 - Prob. 93ECh. 5.1 - How do we measure the distance between two points,...Ch. 5.1 - Prob. 95ECh. 5.1 - Prob. 96ECh. 5.1 - Prob. 97ECh. 5.1 - 98. A Ferris wheel has a radius of 25 feet. The...Ch. 5.1 - Prob. 99ECh. 5.1 - On a carousel, the outer row of animals is 20 feet...Ch. 5.1 - Prob. 101ECh. 5.1 - Prob. 102ECh. 5.1 - 103. Describe an angle in standard position.
Ch. 5.1 - Prob. 104ECh. 5.1 - Prob. 105ECh. 5.1 - Prob. 106ECh. 5.1 - Describe how to convert an angle in degrees to...Ch. 5.1 - Prob. 108ECh. 5.1 - Prob. 109ECh. 5.1 - If a carousel is rotating at 2.5 revolutions per...Ch. 5.1 - Prob. 111ECh. 5.1 - 112. Have you ever noticed that we use the...Ch. 5.1 - Prob. 113ECh. 5.1 - In Exercises 1 13-116, use the keys on your...Ch. 5.1 - Prob. 115ECh. 5.1 - In Exercises 113-116, use the keys on your...Ch. 5.1 - Make Sense? In Exercises 117-120, determine...Ch. 5.1 - Prob. 118ECh. 5.1 - Prob. 119ECh. 5.1 - Prob. 120ECh. 5.1 - Prob. 121ECh. 5.1 - Prob. 122ECh. 5.1 - Prob. 123ECh. 5.1 - Prob. 124ECh. 5.1 - Prob. 125ECh. 5.1 - Prob. 126ECh. 5.1 - Prob. 127ECh. 5.1 - Prob. 128ECh. 5.1 - Prob. 129ECh. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Prob. 6CVCCh. 5.2 - Prob. 7CVCCh. 5.2 - In Exercises 1-8, use the Pythagorean Theorem to...Ch. 5.2 - In Exercises 1-8, use the Pythagorean Theorem to...Ch. 5.2 - In Exercises 1-8 use the Pythagorean Theorem to...Ch. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - In Exercises 1-8, use the Pythagorean Theorem to...Ch. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - In Exercises 9-16, use the given triangles to...Ch. 5.2 - In Exercises 9-16, use the given triangles to...Ch. 5.2 - Prob. 12ECh. 5.2 - In Exercises 9-16, use the given triangles to...Ch. 5.2 - Prob. 14ECh. 5.2 - In Exercises 9-16, use the given triangles to...Ch. 5.2 - In Exercises 9-16, use the given triangles to...Ch. 5.2 - In Exercises 17-20, is an acute angle and and ...Ch. 5.2 - In Exercises 17-20, is an acute angle and and...Ch. 5.2 - In Exercises 17-20, is an acute angle and and ...Ch. 5.2 - In Exercises 17-20, is an acute angle and sin and...Ch. 5.2 - In Exercises 21-24. is an acute angle and sin is...Ch. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - In Exercises 25-30, use an identity to find the...Ch. 5.2 - In Exercises 25-30, use an identity to find the...Ch. 5.2 - In Exercises 25-30, use an identity to find the...Ch. 5.2 - Prob. 28ECh. 5.2 - In Exercises 25-30, use an identity to find the...Ch. 5.2 - In Exercises 25-30, use an identity to find the...Ch. 5.2 - In Exercises 31-38, find a cofunction with the...Ch. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - In Exercises 31-38, find a cofunction with the...Ch. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - In Exercises 39-48, use a calculator to find the...Ch. 5.2 - In Exercises 39-48, use a calculator to find the...Ch. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - In Exercises 49-54, find the measure of the side...Ch. 5.2 - In Exercises 49-54, find the measure of the side...Ch. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - In Exercises 55-58, use a calculator to find the...Ch. 5.2 - In Exercises 55-58, use a calculator to find the...Ch. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - In Exercises 59-62, use a calculator to find the...Ch. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - In Exercises 63-68, find the exact value of each...Ch. 5.2 - In Exercises 63-68, find the exact value of each...Ch. 5.2 - In Exercises 63-68, find the exact value of each...Ch. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - If is an acute angle and cos=13, find csc(2).Ch. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - A tower that is 125 feet tall casts a shadow 172...Ch. 5.2 - The Washington Monument is 555 feet high. If you...Ch. 5.2 - Prob. 77ECh. 5.2 - A road is inclined at an angle of 5. After driving...Ch. 5.2 - Prob. 79ECh. 5.2 - A telephone pole is 55 feet tall. A guy wire 80...Ch. 5.2 - Prob. 81ECh. 5.2 - Prob. 82ECh. 5.2 - Prob. 83ECh. 5.2 - Prob. 84ECh. 5.2 - Prob. 85ECh. 5.2 - 86. Use words (not an equation) to describe one of...Ch. 5.2 - Prob. 87ECh. 5.2 - Prob. 88ECh. 5.2 - Describe a relationship among trigonometric...Ch. 5.2 - Prob. 90ECh. 5.2 - Prob. 91ECh. 5.2 - Use a calculator in the radian mode to fill in the...Ch. 5.2 - Prob. 93ECh. 5.2 - Prob. 94ECh. 5.2 - Prob. 95ECh. 5.2 - Prob. 96ECh. 5.2 - Prob. 97ECh. 5.2 - In Exercises 98-101, determine whether each...Ch. 5.2 - Prob. 99ECh. 5.2 - Prob. 100ECh. 5.2 - Prob. 101ECh. 5.2 - Prob. 102ECh. 5.2 - Prob. 103ECh. 5.2 - 104. From the top of a 250-foot lighthouse, a...Ch. 5.2 - Prob. 105ECh. 5.2 - Prob. 106ECh. 5.2 - Prob. 107ECh. 5.2 - Prob. 108ECh. 5.2 - Exercises 108-110 will help you prepare for the...Ch. 5.2 - Prob. 110ECh. 5.3 - Fill in each blank so that the resulting statement...Ch. 5.3 - Prob. 2CVCCh. 5.3 - Fill in each blank so that the resulting statement...Ch. 5.3 - Prob. 4CVCCh. 5.3 - Prob. 5CVCCh. 5.3 - Prob. 6CVCCh. 5.3 - Fill in each blank so that the resulting statement...Ch. 5.3 - In Exercises 1-8, a point on the terminal side of...Ch. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - In Exercises 1-8, a point on the terminal side of...Ch. 5.3 - In Exercises 9-16, evaluate the trigonometric...Ch. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - In Exercises 17-22, let be an angle in standard...Ch. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - In Exercises 17-22, let be an angle in standard...Ch. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - In Exercises 23-34, find the exact value of each...Ch. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - In Exercises 23-34, find the exact value of each...Ch. 5.3 - In Exercises 23-34, find the exact value of each...Ch. 5.3 - In Exercises 23-34, find the exact value of each...Ch. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - In Exercises 35-60, find the reference angle for...Ch. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 80ECh. 5.3 - Prob. 81ECh. 5.3 - Prob. 82ECh. 5.3 - Prob. 83ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 85ECh. 5.3 - In Exercises 61-86, use reference angles to find...Ch. 5.3 - Prob. 87ECh. 5.3 - Prob. 88ECh. 5.3 - Prob. 89ECh. 5.3 - In Exercises 87-92, find the exact value of each...Ch. 5.3 - Prob. 91ECh. 5.3 - Prob. 92ECh. 5.3 - Prob. 93ECh. 5.3 - Prob. 94ECh. 5.3 - Prob. 95ECh. 5.3 - Prob. 96ECh. 5.3 - In Exercises 93-98, let
.
Find the exact value of...Ch. 5.3 - Prob. 98ECh. 5.3 - In Exercises 99-104, find two values of ,02, that...Ch. 5.3 - Prob. 100ECh. 5.3 - Prob. 101ECh. 5.3 - Prob. 102ECh. 5.3 - Prob. 103ECh. 5.3 - Prob. 104ECh. 5.3 - Prob. 105ECh. 5.3 - Prob. 106ECh. 5.3 - Prob. 107ECh. 5.3 - Prob. 108ECh. 5.3 - Prob. 109ECh. 5.3 - Prob. 110ECh. 5.3 - Prob. 111ECh. 5.3 - Prob. 112ECh. 5.3 - Prob. 113ECh. 5.3 - 114. Graph:
(Section 3.5, Example 6)
Ch. 5.3 - Simplify: 5log519+log773. (Section 4.2, Example 5)Ch. 5.3 - Prob. 116ECh. 5.3 - Prob. 117ECh. 5.3 - Prob. 118ECh. 5.3 - Prob. 119ECh. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Prob. 4CVCCh. 5.4 - Prob. 5CVCCh. 5.4 - Prob. 6CVCCh. 5.4 - Prob. 7CVCCh. 5.4 - Prob. 8CVCCh. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - In Exercises 1-4, a point P(x, y) is shown on the...Ch. 5.4 - In Exercises 1-4, a point P(x, y) is shown on the...Ch. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - In Exercises 19-24. a. Use the unit circle shown...Ch. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - In Exercises 33-42, let sint=a,cost=b,andtant=c....Ch. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - The height of the water, H, in feet, at a boat...Ch. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Describe a phenomenon that repeats indefinitely....Ch. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Prob. 57ECh. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - The seats of a Ferris wheel are 40 feet from the...Ch. 5.4 - Prob. 64ECh. 5.4 - Prob. 65ECh. 5.4 - 63. Use the exponential growth model, , to solve...Ch. 5.4 - Prob. 67ECh. 5.4 - Prob. 68ECh. 5.4 - Prob. 69ECh. 5.5 - Fill in each blank so that the resulting statement...Ch. 5.5 - Prob. 2CVCCh. 5.5 - Fill in each blank so that the resulting statement...Ch. 5.5 - Fill in each blank so that the resulting statement...Ch. 5.5 - Prob. 5CVCCh. 5.5 - Prob. 6CVCCh. 5.5 - Prob. 7CVCCh. 5.5 - Prob. 8CVCCh. 5.5 - Prob. 9CVCCh. 5.5 - Prob. 10CVCCh. 5.5 - Prob. 1ECh. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - In Exercises 7-16, determine the amplitude and...Ch. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - In Exercises 17-30, determine the amplitude,...Ch. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.5 - Prob. 48ECh. 5.5 - Prob. 49ECh. 5.5 - Prob. 50ECh. 5.5 - Prob. 51ECh. 5.5 - Prob. 52ECh. 5.5 - Prob. 53ECh. 5.5 - Prob. 54ECh. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Prob. 57ECh. 5.5 - Prob. 58ECh. 5.5 - Prob. 59ECh. 5.5 - Prob. 60ECh. 5.5 - In Exercises 61-66, find an equation for each...Ch. 5.5 - In Exercises 61-66, find an equation for each...Ch. 5.5 - In Exercises 61-66, find an equation for each...Ch. 5.5 - In Exercises 61-66, find an equation for each...Ch. 5.5 - Prob. 65ECh. 5.5 - In Exercises 61-66, find an equation for each...Ch. 5.5 - Prob. 67ECh. 5.5 - Prob. 68ECh. 5.5 - Prob. 69ECh. 5.5 - Prob. 70ECh. 5.5 - Prob. 71ECh. 5.5 - Prob. 72ECh. 5.5 - Prob. 73ECh. 5.5 - Prob. 74ECh. 5.5 - Prob. 75ECh. 5.5 - Prob. 76ECh. 5.5 - Prob. 77ECh. 5.5 - In the theory of biorhythms, sine functions are...Ch. 5.5 - Prob. 79ECh. 5.5 - Prob. 80ECh. 5.5 - Prob. 81ECh. 5.5 - Prob. 82ECh. 5.5 - Prob. 83ECh. 5.5 - Prob. 84ECh. 5.5 - Prob. 85ECh. 5.5 - Prob. 86ECh. 5.5 - The following figure shows the depth of water at...Ch. 5.5 - Prob. 88ECh. 5.5 - Prob. 89ECh. 5.5 - Prob. 90ECh. 5.5 - Prob. 91ECh. 5.5 - Prob. 92ECh. 5.5 - Prob. 93ECh. 5.5 - Prob. 94ECh. 5.5 - Prob. 95ECh. 5.5 - Prob. 96ECh. 5.5 - Biorhythm cycles provide interesting applications...Ch. 5.5 - Prob. 98ECh. 5.5 - Prob. 99ECh. 5.5 - Prob. 100ECh. 5.5 - Prob. 101ECh. 5.5 - Prob. 102ECh. 5.5 - Prob. 103ECh. 5.5 - Prob. 104ECh. 5.5 - Prob. 105ECh. 5.5 - Prob. 106ECh. 5.5 - Prob. 107ECh. 5.5 - Prob. 108ECh. 5.5 - Prob. 109ECh. 5.5 - Prob. 110ECh. 5.5 - Prob. 111ECh. 5.5 - Prob. 112ECh. 5.5 - Make Sense? In Exercises 111-114, determine...Ch. 5.5 - Prob. 114ECh. 5.5 - Determine the range of each of the following...Ch. 5.5 - Write the equation for a cosine function with...Ch. 5.5 - Prob. 117ECh. 5.5 - Prob. 118ECh. 5.5 - Prob. 120ECh. 5.5 - Prob. 121ECh. 5.5 - Prob. 122ECh. 5.5 - Prob. 123ECh. 5.5 - Prob. 124ECh. 5.5 - Prob. 125ECh. 5.6 - Fill in each blank so that the resulting statement...Ch. 5.6 - Prob. 2CVCCh. 5.6 - Prob. 3CVCCh. 5.6 - Prob. 4CVCCh. 5.6 - Prob. 5CVCCh. 5.6 - Prob. 6CVCCh. 5.6 - Prob. 7CVCCh. 5.6 - Prob. 8CVCCh. 5.6 - In Exercises 1-4. the graph of a tangent function...Ch. 5.6 - In Exercises 1-4, the graph of a tangent function...Ch. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - In Exercises 13-16, the graph of a cotangent...Ch. 5.6 - In Exercises 13-16, the graph of a cotangent...Ch. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - In Exercises 17-24, graph two periods of the given...Ch. 5.6 - Prob. 20ECh. 5.6 - In Exercises 17-24, graph two periods of the given...Ch. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - Prob. 27ECh. 5.6 - Prob. 28ECh. 5.6 - Prob. 29ECh. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Prob. 32ECh. 5.6 - Prob. 33ECh. 5.6 - Prob. 34ECh. 5.6 - Prob. 35ECh. 5.6 - Prob. 36ECh. 5.6 - Prob. 37ECh. 5.6 - Prob. 38ECh. 5.6 - Prob. 39ECh. 5.6 - Prob. 40ECh. 5.6 - Prob. 41ECh. 5.6 - Prob. 42ECh. 5.6 - Prob. 43ECh. 5.6 - Prob. 44ECh. 5.6 - Prob. 45ECh. 5.6 - Prob. 46ECh. 5.6 - Prob. 47ECh. 5.6 - Prob. 48ECh. 5.6 - Prob. 49ECh. 5.6 - Prob. 50ECh. 5.6 - Prob. 51ECh. 5.6 - Prob. 52ECh. 5.6 - Prob. 53ECh. 5.6 - Prob. 54ECh. 5.6 - Prob. 55ECh. 5.6 - Prob. 56ECh. 5.6 - Prob. 57ECh. 5.6 - Prob. 58ECh. 5.6 - Prob. 59ECh. 5.6 - Prob. 60ECh. 5.6 - Prob. 61ECh. 5.6 - In Exercises 62-64, sketch a reasonable graph that...Ch. 5.6 - Prob. 63ECh. 5.6 - Prob. 64ECh. 5.6 - Prob. 65ECh. 5.6 - Prob. 66ECh. 5.6 - Prob. 67ECh. 5.6 - Prob. 68ECh. 5.6 - Prob. 69ECh. 5.6 - Prob. 70ECh. 5.6 - 71. Explain how to use a sine curve to obtain a...Ch. 5.6 - 72. Scientists record brain activity by attaching...Ch. 5.6 - Prob. 73ECh. 5.6 - Prob. 74ECh. 5.6 - Prob. 75ECh. 5.6 - Prob. 76ECh. 5.6 - Prob. 77ECh. 5.6 - Prob. 78ECh. 5.6 - Prob. 79ECh. 5.6 - Prob. 80ECh. 5.6 - Prob. 81ECh. 5.6 - Prob. 82ECh. 5.6 - Prob. 83ECh. 5.6 - Prob. 84ECh. 5.6 - Prob. 85ECh. 5.6 - Prob. 86ECh. 5.6 - Prob. 87ECh. 5.6 - Prob. 88ECh. 5.6 - Prob. 89ECh. 5.6 - Make Sense? In Exercises 89-92, determine whether...Ch. 5.6 - Prob. 91ECh. 5.6 - Make Sense? In Exercises 89-92, determine whether...Ch. 5.6 - Prob. 93ECh. 5.6 - Prob. 94ECh. 5.6 - Prob. 95ECh. 5.6 - Prob. 96ECh. 5.6 - Prob. 97ECh. 5.6 - Prob. 98ECh. 5.6 - Prob. 99ECh. 5.6 - The toll to a bridge costs $8.00. Commuters who...Ch. 5.6 - Write the point-slope form and the slope-intercept...Ch. 5.6 - Prob. 102ECh. 5.6 - Prob. 103ECh. 5.6 - Prob. 104ECh. 5.7 - Fill in each blank so that the resulting statement...Ch. 5.7 - Fill in each blank so that the resulting statement...Ch. 5.7 - Fill in each blank so that the resulting statement...Ch. 5.7 - Fill in each blank so that the resulting statement...Ch. 5.7 - Prob. 5CVCCh. 5.7 - Prob. 6CVCCh. 5.7 - Prob. 7CVCCh. 5.7 - Fill in each blank so that the resulting statement...Ch. 5.7 - Prob. 9CVCCh. 5.7 - Prob. 10CVCCh. 5.7 - Prob. 11CVCCh. 5.7 - Prob. 12CVCCh. 5.7 - Prob. 1ECh. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - Prob. 12ECh. 5.7 - Prob. 13ECh. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - Prob. 15ECh. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - In Exercises 1-18, find the exact value of each...Ch. 5.7 - Prob. 19ECh. 5.7 - Prob. 20ECh. 5.7 - Prob. 21ECh. 5.7 - Prob. 22ECh. 5.7 - Prob. 23ECh. 5.7 - Prob. 24ECh. 5.7 - Prob. 25ECh. 5.7 - Prob. 26ECh. 5.7 - Prob. 27ECh. 5.7 - In Exercises 19-30, use a calculator to find the...Ch. 5.7 - In Exercises 19-30, use a calculator to find the...Ch. 5.7 - Prob. 30ECh. 5.7 - Prob. 31ECh. 5.7 - Prob. 32ECh. 5.7 - Prob. 33ECh. 5.7 - Prob. 34ECh. 5.7 - Prob. 35ECh. 5.7 - Prob. 36ECh. 5.7 - Prob. 37ECh. 5.7 - In Exercises 19-30, use a calculator to find the...Ch. 5.7 - Prob. 39ECh. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - Prob. 42ECh. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - Prob. 44ECh. 5.7 - Prob. 45ECh. 5.7 - Prob. 46ECh. 5.7 - Prob. 47ECh. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - Prob. 49ECh. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - In Exercises 31-46, find the exact value of each...Ch. 5.7 - Prob. 55ECh. 5.7 - Prob. 56ECh. 5.7 - Prob. 57ECh. 5.7 - Prob. 58ECh. 5.7 - Prob. 59ECh. 5.7 - Prob. 60ECh. 5.7 - Prob. 61ECh. 5.7 - Prob. 62ECh. 5.7 - Prob. 63ECh. 5.7 - In Exercises 47-62, use a sketch to find the exact...Ch. 5.7 - Prob. 65ECh. 5.7 - Prob. 66ECh. 5.7 - Prob. 67ECh. 5.7 - Prob. 68ECh. 5.7 - Prob. 69ECh. 5.7 - Prob. 70ECh. 5.7 - Prob. 71ECh. 5.7 - In Exercises 47-62, use a sketch to find the exact...Ch. 5.7 - Prob. 73ECh. 5.7 - Prob. 74ECh. 5.7 - In Exercises 47-62, use a sketch to find the exact...Ch. 5.7 - In Exercises 47-62, use a sketch to find the exact...Ch. 5.7 - Prob. 77ECh. 5.7 - In Exercises 47-62, use a sketch to find the exact...Ch. 5.7 - Prob. 79ECh. 5.7 - Prob. 80ECh. 5.7 - Prob. 81ECh. 5.7 - Prob. 82ECh. 5.7 - Prob. 83ECh. 5.7 - Prob. 84ECh. 5.7 - Prob. 85ECh. 5.7 - In Exercises 63-72, use a right triangle to write...Ch. 5.7 - Prob. 87ECh. 5.7 - Prob. 88ECh. 5.7 - In Exercises 63-72, use a right triangle to write...Ch. 5.7 - Prob. 90ECh. 5.7 - Prob. 91ECh. 5.7 - Prob. 92ECh. 5.7 - Prob. 93ECh. 5.7 - Prob. 94ECh. 5.7 - Prob. 95ECh. 5.7 - 74. a. Graph the restricted cotangent function, ,...Ch. 5.7 - Prob. 97ECh. 5.7 - Prob. 98ECh. 5.7 - Prob. 99ECh. 5.7 - The graphs of y=sin1x,y=cos1x, and y=tan1x are...Ch. 5.7 - Prob. 101ECh. 5.7 - Prob. 102ECh. 5.7 - Prob. 103ECh. 5.7 - Prob. 104ECh. 5.7 - Prob. 105ECh. 5.7 - Prob. 106ECh. 5.7 - Prob. 107ECh. 5.7 - Prob. 108ECh. 5.7 - Prob. 109ECh. 5.7 - Prob. 110ECh. 5.7 - Prob. 111ECh. 5.7 - Prob. 112ECh. 5.7 - Prob. 113ECh. 5.7 - Prob. 114ECh. 5.7 - Prob. 115ECh. 5.7 - Prob. 116ECh. 5.7 - gives the viewing angle, , in radians, for a...Ch. 5.7 - Prob. 118ECh. 5.7 - Prob. 119ECh. 5.7 - Prob. 120ECh. 5.7 - Prob. 121ECh. 5.7 - Prob. 122ECh. 5.7 - Prob. 123ECh. 5.7 - Prob. 124ECh. 5.7 - Prob. 125ECh. 5.7 - Prob. 126ECh. 5.7 - Prob. 127ECh. 5.7 - Prob. 128ECh. 5.7 - Prob. 129ECh. 5.7 - Prob. 130ECh. 5.7 - Prob. 131ECh. 5.7 - Prob. 132ECh. 5.7 - Prob. 133ECh. 5.7 - Prob. 134ECh. 5.7 - Prob. 135ECh. 5.7 - Prob. 136ECh. 5.7 - Prob. 137ECh. 5.7 - Prob. 138ECh. 5.7 - Prob. 139ECh. 5.7 - Prob. 140ECh. 5.7 - Prob. 141ECh. 5.7 - Prob. 142ECh. 5.7 - Prob. 143ECh. 5.7 - Prob. 144ECh. 5.7 - Prob. 145ECh. 5.7 - Prob. 146ECh. 5.7 - Prob. 147ECh. 5.7 - Prob. 148ECh. 5.7 - Prob. 149ECh. 5.7 - Prob. 150ECh. 5.7 - Prob. 151ECh. 5.7 - Prob. 152ECh. 5.7 - Prob. 153ECh. 5.7 - Prob. 154ECh. 5.7 - Prob. 155ECh. 5.8 - Fill in each blank so that the resulting statement...Ch. 5.8 - Prob. 2CVCCh. 5.8 - Prob. 3CVCCh. 5.8 - Prob. 1ECh. 5.8 - Prob. 2ECh. 5.8 - In Exercises 1-12, solve the right triangle shown...Ch. 5.8 - Prob. 4ECh. 5.8 - Prob. 5ECh. 5.8 - Prob. 6ECh. 5.8 - In Exercises 1-12, solve the right triangle shown...Ch. 5.8 - Prob. 8ECh. 5.8 - Prob. 9ECh. 5.8 - Prob. 10ECh. 5.8 - In Exercises 1-12, solve the right triangle shown...Ch. 5.8 - Prob. 12ECh. 5.8 - Prob. 13ECh. 5.8 - Use the figure shown to solve Exercises...Ch. 5.8 - Use the figure shown to solve Exercises...Ch. 5.8 - Prob. 16ECh. 5.8 - In Exercises 17-20, an object is attached to a...Ch. 5.8 - In Exercises 17-20, an object is attached to a...Ch. 5.8 - In Exercises 17-20, an object is attached to a...Ch. 5.8 - Prob. 20ECh. 5.8 - In Exercises 21-28, an object moves in simple...Ch. 5.8 - Prob. 22ECh. 5.8 - Prob. 23ECh. 5.8 - Prob. 24ECh. 5.8 - In Exercises 21-28, an object moves in simple...Ch. 5.8 - Prob. 26ECh. 5.8 - Prob. 27ECh. 5.8 - Prob. 28ECh. 5.8 - In Exercises 29-36, find the length x to the...Ch. 5.8 - Prob. 30ECh. 5.8 - In Exercises 29-36, find the length x to the...Ch. 5.8 - Prob. 32ECh. 5.8 - In Exercises 29-36 find the length x to the...Ch. 5.8 - In Exercises 29-36, find the length x to the...Ch. 5.8 - In Exercises 29-36, find the length x to the...Ch. 5.8 - In Exercises 29-36, find the length x to the...Ch. 5.8 - Prob. 37ECh. 5.8 - In Exercises 37-40, an object moves in simple...Ch. 5.8 - Prob. 39ECh. 5.8 - Prob. 40ECh. 5.8 - 41. The tallest television transmitting tower in...Ch. 5.8 - Prob. 42ECh. 5.8 - 43. The Statue of Liberty is approximately 305...Ch. 5.8 - 44. A 200-foot cliff drops vertically into the...Ch. 5.8 - Prob. 45ECh. 5.8 - Prob. 46ECh. 5.8 - Prob. 47ECh. 5.8 - Prob. 48ECh. 5.8 - Prob. 49ECh. 5.8 - 50. A flagpole is situated on top of a building....Ch. 5.8 - Prob. 51ECh. 5.8 - Prob. 52ECh. 5.8 - Prob. 53ECh. 5.8 - A ship sights a lighthouse directly to the south....Ch. 5.8 - Prob. 55ECh. 5.8 - Prob. 56ECh. 5.8 - Prob. 57ECh. 5.8 - Prob. 58ECh. 5.8 - Prob. 59ECh. 5.8 - Prob. 60ECh. 5.8 - Prob. 61ECh. 5.8 - Prob. 62ECh. 5.8 - Prob. 63ECh. 5.8 - Prob. 64ECh. 5.8 - Prob. 65ECh. 5.8 - Prob. 66ECh. 5.8 - Prob. 67ECh. 5.8 - Prob. 68ECh. 5.8 - Prob. 69ECh. 5.8 - Prob. 70ECh. 5.8 - Prob. 71ECh. 5.8 - Prob. 72ECh. 5.8 - Prob. 73ECh. 5.8 - Prob. 74ECh. 5.8 - Make Sense? In Exercises 72-75, determine whether...Ch. 5.8 - Prob. 76ECh. 5.8 - 77. The angle of elevation to the top of a...Ch. 5.8 - Music and mathematics have been linked over the...Ch. 5.8 - You invested $3000 in two accounts paying 6% and...Ch. 5.8 - Solve: (x1)2=5. (Section 15. Example 2)Ch. 5.8 - 81. Graph: . (Section 2.3, Example 4)
Ch. 5.8 - Exercises 82-84 will help you prepare for the...Ch. 5.8 - Exercises 82 |O-84 will help you prepare for the...Ch. 5.8 - Exercises 82-84 will help you prepare for the...Ch. 5 - In Exercises 1-2 convert each angle in degrees to...Ch. 5 - In Exercises 1-2, convert each angle in degrees to...Ch. 5 - In Exercises 3-4, convert each angle in radians to...Ch. 5 - In Exercises 3-4, convert each angle in radians to...Ch. 5 - Prob. 5MCCPCh. 5 - Prob. 6MCCPCh. 5 - In Exercises 5-7,
a. Find a positive angle less...Ch. 5 - Prob. 8MCCPCh. 5 - Prob. 9MCCPCh. 5 - Prob. 10MCCPCh. 5 - Prob. 11MCCPCh. 5 - Prob. 12MCCPCh. 5 - Prob. 13MCCPCh. 5 - Prob. 14MCCPCh. 5 - Prob. 15MCCPCh. 5 - Prob. 16MCCPCh. 5 - Prob. 17MCCPCh. 5 - Prob. 18MCCPCh. 5 - Prob. 19MCCPCh. 5 - Prob. 20MCCPCh. 5 - Prob. 21MCCPCh. 5 - Prob. 22MCCPCh. 5 - Prob. 23MCCPCh. 5 - Prob. 24MCCPCh. 5 - Prob. 25MCCPCh. 5 - Prob. 26MCCPCh. 5 - Prob. 27MCCPCh. 5 - Prob. 28MCCPCh. 5 - Prob. 29MCCPCh. 5 - Prob. 30MCCPCh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - In Exercises 13-17, find a positive angle less...Ch. 5 - Prob. 15RECh. 5 - In Exercises 13-17, find a positive angle less...Ch. 5 - In Exercises 13-17, find a positive angle less...Ch. 5 - Find the length of the arc on a circle of radius...Ch. 5 - The angular speed of a propeller on a wind...Ch. 5 - 20. The propeller of an airplane has a radius of 3...Ch. 5 - 21. Use the triangle to find each of the six...Ch. 5 - In Exercises 22-25, find the exact value of each...Ch. 5 - In Exercises 22-25, find the exact value of each...Ch. 5 - In Exercises 22-25, find the exact value of each...Ch. 5 - In Exercises 22-25, find the exact value of each...Ch. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - A hiker climbs for a half mile up a slope whose...Ch. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - In Exercises 36-37, a point on the terminal side...Ch. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - In Exercises 43-47, find the reference angle for...Ch. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - In Exercises 48-58 find the exact value of each...Ch. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - In Exercises 59-64, determine the amplitude and...Ch. 5 - In Exercises 65-69, determine the amplitude,...Ch. 5 - In Exercises 65-69, determine the amplitude,...Ch. 5 - In Exercises 65-69, determine the amplitude,...Ch. 5 - In Exercises 65-69, determine the amplitude,...Ch. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - The function y=98.6+0.3sin(12x1112) models...Ch. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Prob. 76RECh. 5 - In Exercises 74-80, graph two full periods of the...Ch. 5 - In Exercises 74-80, graph two full periods of the...Ch. 5 - Prob. 79RECh. 5 - Prob. 80RECh. 5 - Prob. 81RECh. 5 - In Exercises 81-84, graph two full periods of the...Ch. 5 - Prob. 83RECh. 5 - Prob. 84RECh. 5 - Prob. 85RECh. 5 - Prob. 86RECh. 5 - Prob. 87RECh. 5 - Prob. 88RECh. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Prob. 92RECh. 5 - Prob. 93RECh. 5 - Prob. 94RECh. 5 - Prob. 95RECh. 5 - Prob. 96RECh. 5 - Prob. 97RECh. 5 - Prob. 98RECh. 5 - In Exercises 85-103, find the exact value of each...Ch. 5 - Prob. 100RECh. 5 - Prob. 101RECh. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Prob. 104RECh. 5 - Prob. 105RECh. 5 - Prob. 106RECh. 5 - Prob. 107RECh. 5 - Prob. 108RECh. 5 - Prob. 109RECh. 5 - Prob. 110RECh. 5 - Prob. 111RECh. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Prob. 114RECh. 5 - Prob. 115RECh. 5 - Prob. 116RECh. 5 - Prob. 117RECh. 5 - Prob. 118RECh. 5 - Prob. 119RECh. 5 - 116. From city A to city B, a plane flies 850...Ch. 5 - Prob. 121RECh. 5 - Prob. 122RECh. 5 - Prob. 123RECh. 5 - Prob. 124RECh. 5 - Prob. 1TCh. 5 - Prob. 2TCh. 5 - Prob. 3TCh. 5 - Prob. 4TCh. 5 - Prob. 5TCh. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - In Exercises 7-12, find the exact value of each...Ch. 5 - In Exercises 7-12, find the exact value of each...Ch. 5 - In Exercises 7-12, find the exact value of each...Ch. 5 - Prob. 12TCh. 5 - Prob. 13TCh. 5 - Prob. 14TCh. 5 - Prob. 15TCh. 5 - Prob. 16TCh. 5 - Prob. 17TCh. 5 - Prob. 18TCh. 5 - Prob. 19TCh. 5 - Prob. 20TCh. 5 - Prob. 21TCh. 5 - Prob. 22TCh. 5 - Prob. 23TCh. 5 - An object moves in simple harmonic motion...Ch. 5 - Why are trigonometric functions ideally suited to...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - Solve each equation or inequality in Exercises...Ch. 5 - f(x)=x9,findf1(x).Ch. 5 - Divide 20x26x29x+10by5x+2Ch. 5 - 9. Write as a single logarithm and evaluate: .
Ch. 5 - Convert 149 radians to degrees.Ch. 5 - 11. Find the maximum number of positive and...Ch. 5 - Prob. 12CRECh. 5 - Prob. 13CRECh. 5 - Prob. 14CRECh. 5 - Prob. 15CRECh. 5 - Prob. 16CRECh. 5 - Prob. 17CRECh. 5 - Prob. 18CRECh. 5 - Prob. 19CRECh. 5 - Prob. 20CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- The function f(x) = log x is transformed to produce g(x) = log (x) – 3. Identify the type of transformation and describe the change. Please type out answerarrow_forwardEach graph below is the graph of a system of three linear equations in three unknowns of the form Ax = b. Determine whether each system has a solution and, if it does, the number of free variables. A. O free variables ✓ B. no solution C. no solution D. no solution E. 1 free variable F. 1 free variablearrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forward
- Solve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forward
- Solve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1arrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5arrow_forwardWrite an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra - Pythagorean Theorem; Author: yaymath;https://www.youtube.com/watch?v=D_y_owf1WsI;License: Standard YouTube License, CC-BY
The Organic Chemistry Tutor; Author: Pythagorean Theorem Explained!;https://www.youtube.com/watch?v=B0G35RkmwSw;License: Standard Youtube License