
Concept explainers
On-time arrivals, lost baggage, and customer complaints are three measures that are typically used to measure the quality of service being offered by airlines. Suppose that the following values represent the on-time arrival percentage, amount of lost baggage, and customer complaints for 10 U.S. airlines.
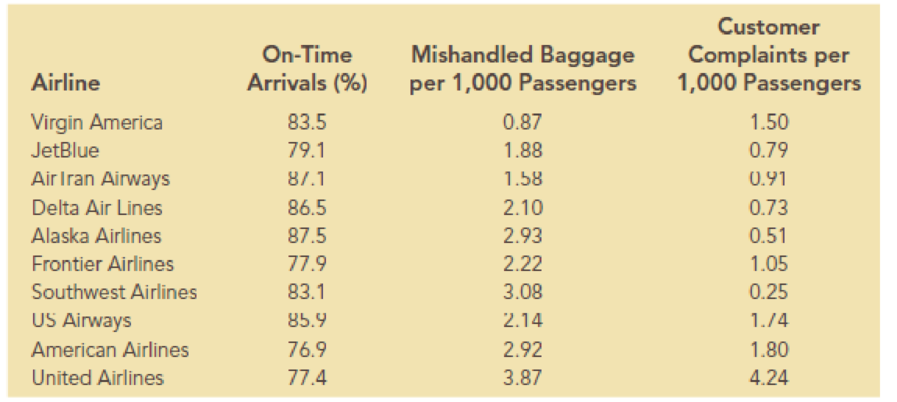
- a. Based on the data above, if you randomly choose a Delta Air Lines flight, what is the
probability that this individual flight will have an on-time arrival? - b. If you randomly choose 1 of the 10 airlines for a follow-up study on airline quality ratings, what is the probability that you will choose an airline with less than two mishandled baggage reports per 1,000 passengers?
- c. If you randomly choose 1 of the 10 airlines for a follow-up study on airline quality ratings, what is the probability that you will choose an airline with more than one customer complaint per 1,000 passengers?
- d. What is the probability that a randomly selected AirTran Airways flight will not arrive on time?
a.
Find the probability that a randomly selected D flight has an on-time arrival.
Answer to Problem 1P
The probability that a randomly selected D flight has an on-time arrival is 0.865.
Explanation of Solution
Calculation:
From the given table, the percentage of D flight has an on-time arrival is 86.5%.
Thus, the probability that a randomly selected D flight has an on-time arrival is 0.865.
b.
Find the probability that a randomly selected airline has less than two mishandled baggage reports per 1,000 passengers.
Answer to Problem 1P
The probability that a randomly selected airline has less than two mishandled baggage reports per 1,000 passengers is 0.3.
Explanation of Solution
Calculation:
From the given table, there are 3 airlines which have less than two mishandled baggage reports per 1,000 passengers. Also, there are 10 airlines.
Define the event A as the airline has less than two mishandled baggage reports per 1,000 passengers.
The required probability is obtained as given below:
Thus, the probability that a randomly selected airline has less than two mishandled baggage reports per 1,000 passengers is 0.3.
c.
Find the probability that a randomly selected airline has more than one customer compliant per 1,000 passengers.
Answer to Problem 1P
The probability that a randomly selected airline has more than one customer compliant per 1,000 passengers is 0.5.
Explanation of Solution
Calculation:
From the given table, there are 5 airlines which have more than one customer compliant.
Define the event B as the airline that has more than one customer compliant per 1,000 passengers.
The required probability is obtained as given below:
Thus, the probability that a randomly selected airline has more than one customer compliant per 1,000 passengers is 0.5.
d.
Find the probability that a randomly selected AT flight does not have an on-time arrival.
Answer to Problem 1P
The probability that a randomly selected AT flight does not have an on-time arrival is 0.129.
Explanation of Solution
Calculation:
From the given table, the percentage of AT flight has an on-time arrival is 87.1%.
Define the event C as AT flight has an on-time arrival.
The required probability is obtained as given below:
Thus, the probability that a randomly selected AT flight does not have an on-time arrival is 0.129.
Want to see more full solutions like this?
Chapter 5 Solutions
Essentials of Business Analytics (MindTap Course List)
- Clint, obviously not in college, sleeps an average of 8 hours per night with a standard deviation of 15 minutes. What's the chance of him sleeping between 7.5 and 8.5 hours on any given night? 0-(7-0) 200 91109s and doiw $20 (8-0) mol 8520 slang $199 galbrog seam side pide & D (newid se od poyesvig as PELEO PER AFTE editiw noudab temand van Czarrow_forwardTimes to complete a statistics exam have a normal distribution with a mean of 40 minutes and standard deviation of 6 minutes. Deshawn's time comes in at the 90th percentile. What percentage of the students are still working on their exams when Deshawn leaves?arrow_forwardSuppose that the weights of cereal boxes have a normal distribution with a mean of 20 ounces and standard deviation of half an ounce. A box that has a standard score of o weighs how much? syed by ilog ni 21arrow_forward
- Bob scores 80 on both his math exam (which has a mean of 70 and standard deviation of 10) and his English exam (which has a mean of 85 and standard deviation of 5). Find and interpret Bob's Z-scores on both exams to let him know which exam (if either) he did bet- ter on. Don't, however, let his parents know; let them think he's just as good at both subjects. algas 70) sering digarrow_forwardSue's math class exam has a mean of 70 with a standard deviation of 5. Her standard score is-2. What's her original exam score?arrow_forwardClint sleeps an average of 8 hours per night with a standard deviation of 15 minutes. What's the chance he will sleep less than 7.5 hours tonight? nut bow visarrow_forward
- Suppose that your score on an exam is directly at the mean. What's your standard score?arrow_forwardOne state's annual rainfall has a normal dis- tribution with a mean of 100 inches and standard deviation of 25 inches. Suppose that corn grows best when the annual rainfall is between 100 and 150 inches. What's the chance of achieving this amount of rainfall? wved now of sociarrow_forward13 Suppose that your exam score has a standard score of 0.90. Does this mean that 90 percent of the other exam scores are lower than yours?arrow_forward
- Bob's commuting times to work have a nor- mal distribution with a mean of 45 minutes and standard deviation of 10 minutes. How often does Bob get to work in 30 to 45 minutes?arrow_forwardBob's commuting times to work have a nor- mal distribution with a mean of 45 minutes and standard deviation of 10 minutes. a. What percentage of the time does Bob get to work in 30 minutes or less? b. Bob's workday starts at 9 a.m. If he leaves at 8 a.m., how often is he late?arrow_forwardSuppose that you want to put fat Fido on a weight-loss program. Before the program, his weight had a standard score of +2 com- pared to dogs of his breed/age, and after the program, his weight has a standard score of -2. His weight before the program was 150 pounds, and the standard deviation for the breed is 5 pounds. a. What's the mean weight for Fido's breed/ age? b. What's his weight after the weight-loss program?arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt




