
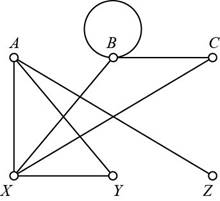
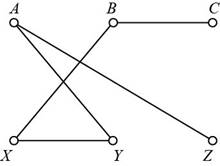
For the graph shown in Fig 5-29,
a. give the vertex set.
b. give the edge list.
c. give the degree of each vertex.
d. draw a version of the graph without crossing points.
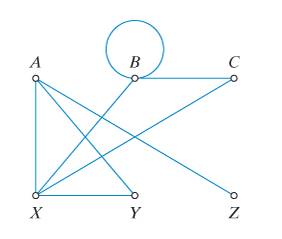
(a)
To find:
The vertex set of given graph.
Answer to Problem 1E
Solution:
The vertex set is
Explanation of Solution
In the graphical representation of routes, the location is defined as a dot in the graph. Those dots are the vertices of the graph and the collection of vertices come under the vertex set.
Given:
The given graph is,
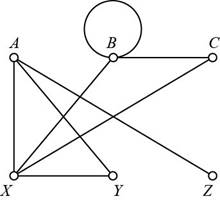
From the given graph, the vertices are
(b)
To find:
The edge list of given graph.
Answer to Problem 1E
Solution:
The list of edges is
Explanation of Solution
Given:
In the graphical representation of routes, the paths or routes are defined by the lines in the graph. Those lines are the edges of the graph.
The given graph is,
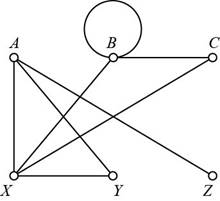
From the given graph, the edges are
(c)
To find:
The degree of each vertex in given graph.
Answer to Problem 1E
Solution:
The degree on vertices are
Explanation of Solution
In the graph theory, the degree of any vertex is the number of edge formed on that particular vertex.
The count for a loop on any vertex is two degree on that vertex.
Given:
The given graph is,
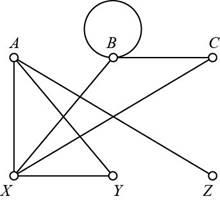
From the given graph, the vertex A has 3 edges adjoined on it. The degree of vertex A is
The vertex B has 4 edges adjoined on it. The degree of vertex B is
The vertex C has 2 edges adjoined on it. The degree of vertex C is
The vertex X has 4 edges adjoined on it. The degree of vertex X is
The vertex Y has 2 edges adjoined on it. The degree of vertex Y is
The vertex Z has 1 edge adjoined on it. The degree of vertex Z is
Conclusion:
Thus, the degree on vertices are
(d)
To plot:
The version of the graph without crossing points
Answer to Problem 1E
Solution:
The required graph is,
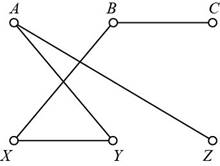
Explanation of Solution
Given:
The given graph is,
The required graph needs to have a route in which no vertex is taken again. From the given graph, the required graph is,
Want to see more full solutions like this?
Chapter 5 Solutions
EXCURSIONS IN MOD.MATH W/ACCESS >BI<
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Precalculus: Mathematics for Calculus (Standalone Book)
Precalculus
Beginning and Intermediate Algebra
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Algebra and Trigonometry (6th Edition)
- PS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forwardskip A swimming pool plan has concrete stairs leading down into the shallow end How much concrete will be needed to build the stairs? Bift 9 ft 2 ft 1 ft 9 ft 2 ft 5 ft [ ? ] ft³arrow_forwardhow to do part b,carrow_forward
- If p = 5 (mod 8), where p is prime, show that p|2 (P-1)/2 + 1. State and prove the corresponding result when p = 7 (mod 8). Deduce that 250 + 1 and 251 1 are composite. -arrow_forwardWhy the character no change for my remark?arrow_forwardDetermine the radius of convergence of a power series:12.6.5, 12.6.6, 12.6.7, 12.6.8Hint: Use Theorem12.5.1 and root test, ratio test, integral testarrow_forward
- In preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forwardTo generate leads for new business, Gustin Investment Services offers free financial planning seminars at major hotels in Southwest Florida. Gustin conducts seminars for groups of 25 individuals. Each seminar costs Gustin $3,700, and the average first-year commission for each new account opened is $5,200. Gustin estimates that for each individual attending the seminar, there is a 0.01 probability that individual will open a new account. (a) Determine the equation for computing Gustin's profit per seminar, given values of the relevant parameters. Profit = (3,700 x 5,200) - New Accounts Opened Profit = 5,200 - (New Accounts Opened x 3,700) Profit = (New Accounts Opened x 3,700) - 5,200 Profit = New Accounts Opened - (5,200 × 3,700) Profit = (New Accounts Opened x 5,200) - 3,700 (b) What type of random variable is the number of new accounts opened? Hint: Review Appendix 12.1 for descriptions of various types of probability distributions. continuous integer uniform normal discrete uniform…arrow_forwardStrassel Investors buys real estate, develops it, and resells it for a profit. A new property is available, and Bud Strassel, the president and owner of Strassel Investors, believes if he purchases and develops this property, it can then be sold for $158,000. The current property owner has asked for bids and stated that the property will be sold for the highest bid in excess of $100,000. Two competitors will be submitting bids for the property. Strassel does not know what the competitors will bid, but he assumes for planning purposes that the amount bid by each competitor will be uniformly distributed between $100,000 and $148,000. (a) What is the estimate of the probability Strassel will be able to obtain the property using a bid of $128,000? (Use at least 5,000 trials. Round your answer three decimal places.) (b) How much does Strassel need to bid to be assured of obtaining the property? $128,000 $138,000 $148,000 (c) Use the simulation model to compute the profit for each trial of…arrow_forward
- Grear Tire Company has produced a new tire with an estimated mean lifetime mileage of 34,500 miles. Management also believes that the standard deviation is 4,500 miles and that tire mileage is normally distributed. To promote the new tire, Grear has offered to refund a portion of the purchase price if the tire fails to reach 30,000 miles before the tire needs to be replaced. Specifically, for tires with a lifetime below 30,000 miles, Grear will refund a customer $1 per 100 miles short of 30,000. Construct a simulation model to answer the following questions. (Use at least 1,000 trials.) (a) For each tire sold, what is the average cost of the promotion (in $)? (Round your answer to two decimal places.) (b) What is the probability that Grear will refund more than $25 for a tire? (Round your answer to three decimal places.)arrow_forwardMajor League Baseball's World Series is a maximum of seven games, with the winner being the first team to win four games. Assume that the Atlanta Braves and the Minnesota Twins are playing in the World Series and that the first two games are to be played in Atlanta, the next three games at the Twins' ballpark, and the last two games, if necessary, back in Atlanta. Taking into account the projected starting pitchers for each game and the home field advantage, suppose the probabilities of Atlanta winning each game are as follows. Game 1 2 3 4 5 6 7 Probability of Win 0.61 0.54 0.47 0.46 0.47 0.56 0.49 Construct a simulation model in which whether Atlanta wins or loses each game is a random variable. Use the model to answer the following questions. (Use at least 1,000 trials.) (a) What is the average number of games played regardless of winner? (Round your answer to one decimal place.) games (b) What is the probability that the Atlanta Braves win the World Series? (Round your answer to…arrow_forward1 Brinkley 2 A B с D E F G H I J 3 Parameters 4 Selling Price 5 Procurement Cost 6 Labor Cost 7 Transportation Cost 8 9 Procurement Cost 10 Lower End of Interval Upper End of Interval Cost Probability 11 $10.00 12 $11.00 0.25 0.45 13 $12.00 0.3 14 15 Labor Cost 16 Lower End of Interval Upper End of Interval Cost Probability 17 $20.00 0.1 18 $22.00 0.25 19 $24.00 0.35 20 $25.00 0.3 21 22 Transportation Cost 23 Lower End of Interval Upper End of Interval Cost Probability 24 25 $3.00 $5.00 0.75 0.25 26 27 Model 28 Profit Per Unit 29 30 Simulation Trial Procurement Cost Labor Cost Transportation Cost Profit Per Unit Summary Statistics 31 1 Mean Profit Per Unit #DIV/0! 32 2 P(Profit <$5) #DIV/0! 83 3 34 4 35 5 36 6 37 7 38 8 39 9 40 10arrow_forward
 Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





