
An electronic chess game has a useful life that is exponential with a mean of 30 month. Determine each of the following:
a. The probability that any given unit will operate for at least (1) 39 months. (2) 48 men the (3) 60 months.
b. The probability that any given unit will fail sooner than (1) 33 months. (2) 15 months. (3) 6 months.
c. The length of service tune after which the percentage of tilled units will approximately equal (1) 50 percent, (2) 85 percent, (3) 95 percent, (4) 99 percent.
a)
To determine: The probability the unit will operate at least for the following times.
Introduction:
Mean time between failures (MTBF):
The mean time between failures is a term which denotes the time that is elapsed between the first failure of a product and the second failure of a product. It is calculated during the normal system operation.
Answer to Problem 12P
1) 39 months = 0.2725
2) 48 months = 0.2019
3) 60 months = 0.1353
Explanation of Solution
Given information:
MTBF = 30 months
Formula to calculate the probability of no failure before a time period:
Calculation of probability:
1) 39 months:
Hence, the probability the unit will operate at least for the 39 months is 0.2725.
2) 48 months:
Hence, the probability the unit will operate at least for the 48 months is 0.2019.
3) 60 months:
Hence, the probability the unit will operate at least for the 60 months is 0.1353.
b)
To determine: The probability the unit will fail before the following times.
Introduction:
Mean time between failures (MTBF):
The mean time between failures is a term which denotes the time that is elapsed between the first failure of a product and the second failure of a product. It is calculated during the normal system operation.
Answer to Problem 12P
1) 33 months = 0.6671
2) 15 months = 0.3935
3) 6 months = 0.1813
Explanation of Solution
Given information:
MTBF = 30 months
Formula to calculate the probability of failure before a time period:
Calculation of probability:
1) 33 months:
Hence, the probability the unit will fail before 33 months is 0.6671.
2) 15 months:
Hence, the probability the unit will fail before 15 months is 0.3935.
3) 6 months:
Hence, the probability the unit will fail before 6 months is 0.1813.
c)
To determine: The length of service time for the percentage of failed units.
Introduction:
Mean time between failures (MTBF):
The mean time between failures is a term which denotes the time that is elapsed between the first failure of a product and the second failure of a product. It is calculated during the normal system operation.
Answer to Problem 12P
1) 50 percent = 21 months.
2) 85 percent = 57 months.
3) 95 percent = 90 months.
4) 99 percent = 138 months.
Explanation of Solution
Given information:
MTBF = 30 months
Formula to calculate the probability of no failure before a time period:
Calculation of probability:
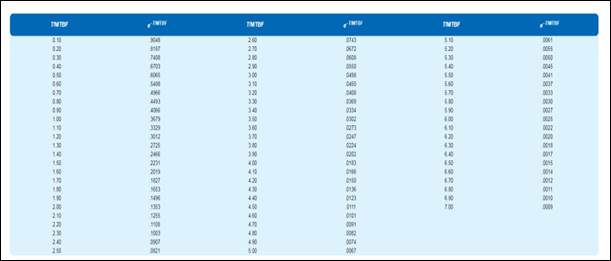
The different probabilities are obtained from the above table.
1) 50 percent:
From the table for the value of 0.50 is equivalent to:
Therefore,
Hence, the length of service time for the percentage of failed units is 21 months.
2) 85 percent:
From the table for the value of 0.15 is equivalent to:
Therefore,
Hence, the length of service time for the percentage of failed units is 57 months.
3) 95 percent:
From the table for the value of 0.05 is equivalent to:
Therefore,
Hence, the length of service time for the percentage of failed units is 90 months.
4) 99 percent:
From the table for the value of 0.01 is equivalent to:
Therefore,
Hence, the length of service time for the percentage of failed units is 138 months.
Want to see more full solutions like this?
Chapter 4 Solutions
Operations Management (Comp. Instructor's Edition)
- Can you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this throughly Here's the what-if scenario: Assume that Dallas plant has lost power. It cannot serve the DCs anymore and has to remain locked indefinitely. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary In comparing the Constraint Scenario to the What-if Scenario, a few key differences highlight the efficiencies evident in the supply chain. Firstly, the total cost in the Constraint Scenario is lower at $7,424,575.45, while the What-if Scenario incurs a total cost of $7,486,369.12, resulting in a cost delta of $61,793.67. Additionally, although both scenarios exhibit the same average service time of 0.72 days, the What-if Scenario has a more favorable average end-to-end service time of 2.41…arrow_forwardEmployee In-Service Training ASSIGNMENT: In-Service Training. The intern is required to plan and implement two in-service training sessions for employees. Each in-service should last at least 10 but not more than 30 minutes and should be given to all employees affected. The preceptor or supervisor/unit manager must approve all in-service topics. 1) One presentation should be related to a policy or procedure of any kind (e.g. proper use of equipment); 2) The second presentation must be related to sanitation or safety. For each in-service presentation, the intern must develop a written class plan and a visual aid (may be a handout, poster, PowerPoint slide presentation, etc.) appropriate to the life experiences, cultural diversity and educational background of the target audience. The intern must also measure behavior change. Note, this cannot be measured by a written pre- and post- test. That would be measuring knowledge. The intern mustactually observe and document that the learners…arrow_forwardFor a dietary manager in a nursing home to train a dietary aidearrow_forward
- Dietary Management in a Nursing Home. As detailed as possible.arrow_forwardFor dietary management in a nursing home. As detailed as possible.arrow_forwardA small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process – assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: T = number of tables produced each week C= number of chairs produced each week According to the above information, what would the objective function be? (a) Maximize T+C (b) Maximize 120T + 80C (c) Maximize 200T+200C (d) Minimize 6T+5C (e) none of the above According to the information provided in Question 17, which of the following would be a necessary constraint in the problem? (a) T+C ≤ 40 (b) T+C ≤ 200 (c) T+C ≤ 180 (d) 120T+80C ≥ 1000…arrow_forward
- As much detail as possible. Dietary Management- Nursing Home Don't add any fill-in-the-blanksarrow_forwardMenu Planning Instructions Use the following questions and points as a guide to completing this assignment. The report should be typed. Give a copy to the facility preceptor. Submit a copy in your Foodservice System Management weekly submission. 1. Are there any federal regulations and state statutes or rules with which they must comply? Ask preceptor about regulations that could prescribe a certain amount of food that must be kept on hand for emergencies, etc. Is the facility accredited by any agency such as Joint Commission? 2. Describe the kind of menu the facility uses (may include standard select menu, menu specific to station, non-select, select, room service, etc.) 3. What type of foodservice does the facility have? This could be various stations to choose from, self-serve, 4. conventional, cook-chill, assembly-serve, etc. Are there things about the facility or system that place a constraint on the menu to be served? Consider how patients/guests are served (e.g. do they serve…arrow_forwardWork with the chef and/or production manager to identify a menu item (or potential menu item) for which a standardized recipe is needed. Record the recipe with which you started and expand it to meet the number of servings required by the facility. Develop an evaluation rubric. Conduct an evaluation of the product. There should be three or more people evaluating the product for quality. Write a brief report of this activity • Product chosen and the reason why it was selected When and where the facility could use the product The standardized recipe sheet or card 。 o Use the facility's format or Design one of your own using a form of your choice; be sure to include the required elements • • Recipe title Yield and portion size Cooking time and temperature Ingredients and quantities Specify AP or EP Procedures (direction)arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

