Chapter 4.EA, Problem 1EA

Suppose that a particular plot of land can sustain 500 deer and that the population of this particular species of deer can be modeled according to the logistic model as

$\frac{dP}{dt}=0.2\left(1-\frac{P}{500}\right)P$.

Each year, a proportion of the herd deer is sold to petting zoos.

a. Find the function that gives the equilibrium population for various proportions.

b. Determine the maximum number of deer that should be sold to petting zoos each year. (Hint: Find the maximum sustainable harvest)

To determine

a.

To find:

The function that represents equilibrium population for various proportions.

Answer to Problem 1EA

Solution:

The function that represents equilibrium population for various proportions is $P^2-500P=0$

Explanation of Solution

Given:

The logistic model for a particular species of deer is given by

$\frac{dP}{dt}=0.2\left(1-\frac{P}{500}\right)P$

Calculation:

The equilibrium population is reached when the logistic model is zero.

$\begin{array}{l}\left(i.e.\right)\frac{dP}{dt}=0\\ 0.2\left(1-\frac{P}{500}\right)P=0\\ 0.2\left(\frac{500-P}{500}\right)P=0\\ 0.2\left(500-P\right)P=0\\ 500P-P^2=0\\ P^2-500P=0\end{array}$

Therefore, the function that represents equilibrium population for various proportions is $P^2-500P=0$

Also, the points at which the equilibrium population can be attained is computed as follows:

$\begin{array}{l}{P}^2-500P=0\\ P\left(P-500\right)=0\\ P=0,P=500\end{array}$

To determine

b.

The maximum number of deer that should be sold each year.

Answer to Problem 1EA

Solution:

The maximum number of deer that should be sold to petting zoos each year is 250.

Explanation of Solution

Given:

The logistic model for a particular species of deer is given by

$\frac{dP}{dt}=0.2\left(1-\frac{P}{500}\right)P$

Calculation:

Using the graphing utility, the graph of the given function is obtained as follows:

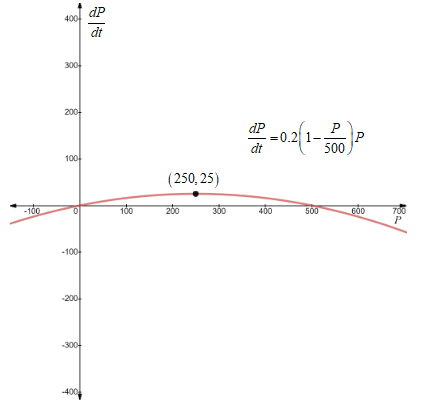
From the graph, it is observed that the function attains its maximum at the point $\left(250,25\right)$.

Hence, the maximum number of deer that should be sold to petting zoos each year is 250 to sustain the population.