Chapter 4.9, Problem 24E

Projectile Motion with Air Resistance Determine a system of differential equations that describes the path of motion in Problem 23 if air resistance is a retarding force k (of magnitude k) acting tangent to the path of the projectile but opposite to its motion. See Figure 4.9.3. Solve the system. [Hint: k is a multiple of velocity, say, βv.]

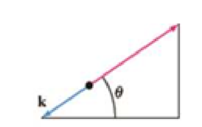
FIGURE 4.9.3 Forces in Problem 24

23. Projectile Motion A projectile shot from a gun has weight w = mg and velocity v tangent to its path of motion. Ignoring air resistance and all other forces acting on the projectile except its weight, determine a system of differential equations that describes its path of motion. See Figure 4.9.2. Solve the system. [Hint. Use Newton’s second law of motion in the x and y directions.]

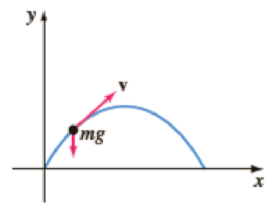
FIGURE 4.9.2 Path of projectile in Problem 23