The position vector ( r ¯ ) , velocity vector ( r ¯ ˙ ) , acceleration vector ( r ¯ ¨ ) , kinetic energy ( T ) , angular momentum vector ( H O ) , and the time rate of angular momentum vector ( H ˙ O ) .

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 4.8, Problem 93RP

To determine

The position vector $(r¯)$ , velocity vector $(r¯˙)$ , acceleration vector $(r¯¨)$ , kinetic energy $(T)$ , angular momentum vector $(HO)$ , and the time rate of angular momentum vector $(H˙O)$ .

Expert Solution & Answer

Answer to Problem 93RP

The position vector $(r¯)$ of the system of particles is $d7(i+4j+6k)$ .

The velocity vector $(r¯˙)$ of the system of particles is $v7(4i+2j+6k)$ .

The acceleration vector $(r¯¨)$ of the system of particles is $(F7m)k$ .

The kinetic energy $(T)$ of the system of particles is $13mv2$ .

The angular momentum vector $(HO)$ of the system about the origin is

$mvd[12i+6j+2k]$ .

The time rate of angular momentum vector $(H˙O)$ of the system of particles is $−(Fd)j$ .

Explanation of Solution

Draw the free body diagram of the system f particles is shown in Figure (1).

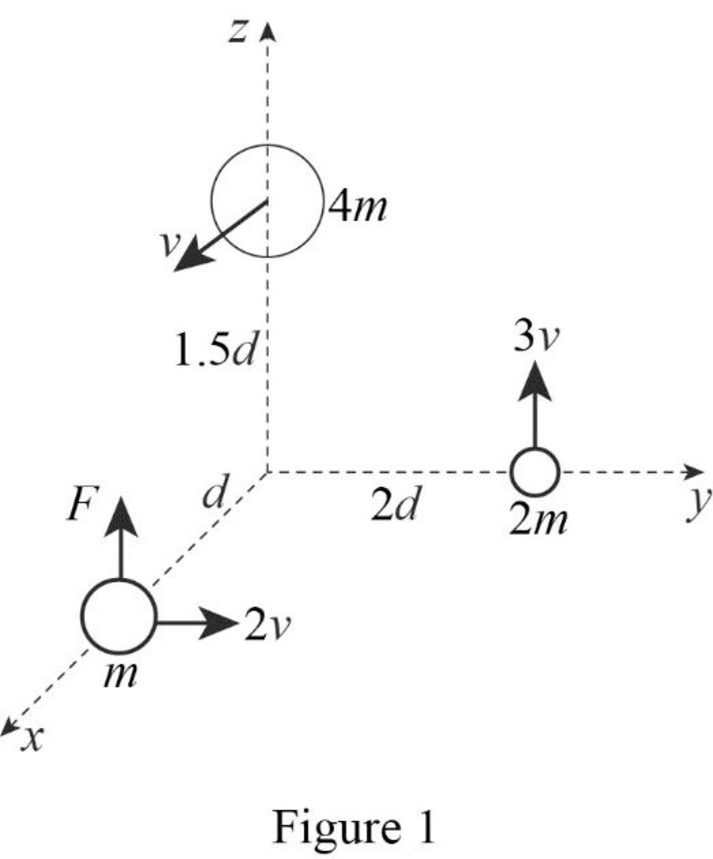
Engineering Mechanics: Dynamics, Chapter 4.8, Problem 93RP

Write the expression to determine the position vector $(r¯)$ of the system of particles.

$r¯=∑miri∑mi=mArA+mBrB+mCrCmA+mB+mC$ (I)

Here, mass of the particles is $mi$ , position of the articles is $ri$ , masses of the particles in positions are $mA$ , $mB$ , and $mC$ , distance between the particles are $rA$ , $rB$ , and $rC$ .

Write the expression to determine the velocity vector $(r¯˙)$ of the system of particles.

$r¯˙=∑mivi∑mi=mAvA+mBvB+mCvCmA+mB+mC$ (II)

Here, velocity acting on the particles is $vi$ .and velocity of the particles are $vA$ , $vB$ , and $vC$ .

Write the expression to determine the acceleration vector $(r¯¨)$ of the system of particles.

$r¯¨=∑Fi∑mi=FA+FB+FCmA+mB+mC$ (III)

Here, the external forces acting on the particles is $Fi$ , and forces of the particles are $FA$ , $FB$ , and $FC$ .

Write the expression to determine the kinetic energy $(T)$ of the system of particles.

$T=∑12mivi=12(mAvA2+mBvB2+mCvC2)$ (IV)

Write the expression to determine the angular momentum vector $(HO)$ of the system about the origin.

$HO=∑(ri×mivi)=(rA×mAvA+rB×mBvB+rC×mCvC)$ (V)

Write the expression to determine time rate of angular momentum vector $(H˙O)$ of the system of particles.

$H˙O=∑MO=∑ri×Fi=(rA×FA)+(rB×FB)+(rC×Fc)$ (VI)

Conclusion:

Susbtitute $4m$ for $mA$ , $2m$ for $mB$ , $m$ for $mC$ , $(1.5d)i$ for $rA$ , $(2d)j$ for $rB$ , and $(d)i$ for $rC$ in Equation (I).

$r¯=[4m×(1.5d)k]+[2m×((2d)j)]+[m×(d)i]4m+2m+m=m[6dk+4dj+di]7m=di+4dj+6dk7=d7(i+4j+6k)$

Thus, position vector $(r¯)$ of the system of particles is $d7(i+4j+6k)$ .

Susbtitute $m$ for $mA$ , $4m$ for $mB$ , $2m$ for $mC$ , $vi$ for $vA$ , $3vk$ for $vB$ , and $2vj$ for $vC$ in Equation (II).

$r¯˙=[4m×(v)i]+[2m×(3v)k]+[m×(2v)j]4m+2m+m=m[(4v)i+(6v)k+(2v)j]7m=(4v)i+(6v)k+(2v)j7=v7(4i+2j+6k)$

Thus, the velocity vector $(r¯˙)$ of the system of particles is $v7(4i+2j+6k)$ .

Susbtitute $4m$ for $mA$ , $2m$ for $mB$ , $m$ for $mC$ , $0$ for $FA$ , $0$ for $FB$ , and $Fk$ for $FC$ in Equation (III).

$r¯¨=(F)k4m+2m+m=(F7m)k$

Thus, the acceleration vector $(r¯¨)$ of the system of particles is $(F7m)k$ .

Susbtitute $4m$ for $mA$ , $2m$ for $mB$ , $m$ for $mC$ , $vi$ for $vA$ , $3vk$ for $vB$ , and $2vj$ for $vC$ in Equation (IV).

$T=12[(4m×v2)+(2m×(3v)2)+(m×(2v)2)]=12(4mv2+18mv2+4mv2)=12(26mv2)=13mv2$

Thus, the kinetic energy $(T)$ of the system of particles is $13mv2$ .

Susbtitute $4m$ for $mA$ , $2m$ for $mB$ , $m$ for $mC$ , $vi$ for $vA$ , $3vk$ for $vB$ , $2vj$ for $vC$ , $(1.5d)i$ for $rA$ , $(2d)j$ for $rB$ , and $(d)i$ for $rC$ in Equation (V).

$HO=[(1.5d)k+(2d)j+(d)i]×[(4m×vi)+(2m×(3v)k)+(m×2v)j]=[(1.5d)k+(2d)j+(d)i]×m[(4vi)+(6v)k+(2v)j]=6mvdj+12mvdi+2mvdk=mvd[12i+6j+2k]$

Thus, the angular momentum vector $(HO)$ of the system about the origin is $mvd[12i+6j+2k]$

Susbtitute $4m$ for $mA$ , $2m$ for $mB$ , $m$ for $mC$ , $0$ for $FA$ , $0$ for $FB$ , and $Fk$ for $FC$ , $(1.5d)i$ for $rA$ , $(2d)j$ for $rB$ , and $(d)i$ for $rC$ in in Equation (VI).

$H˙O=((1.5d)k×0)+[2dj×0]+((d)i×Fk)=0+0+(−Fd)j=−(Fd)j$

Thus, the time rate of angular momentum vector $(H˙O)$ of the system of particles is $−(Fd)j$ .

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Determine the coefficients of polynomial for the polynomial function of Cam profile based on the boundary conditions shown in the figure. S a 3 4 5 C₁ (+) Ꮎ В s = q + q { + c f * + q € * + q ( +c+c+c 6 Ꮎ +C5 +C β В В 0 cam angle 0 B 7 (

### Superheated steam powers a steam turbine for the production of electrical energy. The steam expands in the turbine and at an intermediate expansion pressure (0.1 Mpa) a fraction is extracted for a regeneration process in a surface regenerator. The turbine has an isentropic efficiency of 90% Design the simplified power plant schematic Analyze it on the basis of the attached figure Determine the power generated and the thermal efficiency of the plant ### Dados in the attached images

The machine below forms metal plates through the application of force. Two toggles (ABC and DEF) transfer forces from the central hydraulic cylinder (H) to the plates that will be formed. The toggles then push bar G to the right, which then presses a plate (p) into the cavity, thus shaping it. In this case, the plate becomes a section of a sphere. If the hydraulic cylinder can produce a maximum force of F = 10 kN, then what is the maximum P value (i.e. Pmax) that can be applied to the plate when θ = 35°? Also, what are the compressive forces in the toggle rods in that situation? Finally, what happens to Pmax and the forces in the rods as θ decreases in magnitude?

Answer 2