Chapter 4.8, Problem 33E

Solution

a.

To calculate: The value of b as period is 12 month.

The value of b is $\frac{\pi }{6}$ .

Given Information:

The figure is defined as,

  

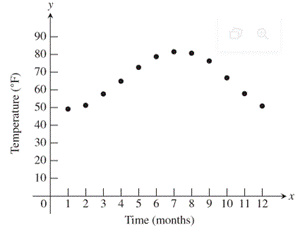
Calculation:

Consider the given polynomial,

Substitute the period in the period formula.

  $\begin{array}{c}\text{Period}=\frac{2\pi }{b}\left[\text{Period}=12\right]\\ b=\frac{2\pi }{12}\\ =\frac{\pi }{6}\end{array}$

Therefore, the obtained value is $\frac{\pi }{6}$ .

b.

To determine: The range of the sinusoid and the value of a and k .

The obtained values are $a=16.15$ and $k=65.35$ .

Given Information:

The figure is defined as,

  

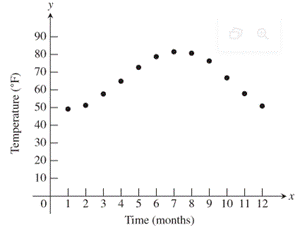
Explanation:

Consider the given information,

The high temperature is $M=81.5°\text{F}$ and the low temperature is $m=49.2°\text{F}$ .

Now, find a .

  $\begin{array}{c}a=\frac{M-m}{2}\\ =\frac{81.5-49.2}{2}\\ =16.15\end{array}$

Now, find k .

  $\begin{array}{c}k=\frac{M+m}{2}\\ =\frac{81.5+49.2}{2}\\ =65.35\end{array}$

Therefore, the obtained values are $a=16.15$ and $k=65.35$ .

c.

To determine: The value of h that will put the minimum at $t=1$ and the maximum at $t=7$ .

The obtained value is 4.

Given Information:

The figure is defined as,

  

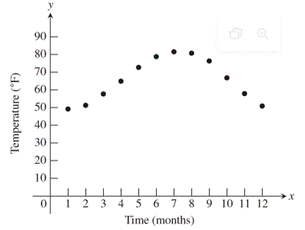
Explanation:

Consider the given information,

As the sine function with $a>0$ , its maximum value occurs at $\frac{1}{4}$ ? of the period. Here, $\frac{1}{4}$ ?of the period is $\frac{1}{4}\left(12\right)=3$ .

The maximum is at $t=7$ and need to shift the graph 3 units to the left such that:

  $\begin{array}{c}h=7-3\\ =4\end{array}$

Therefore, the required value is 4.

d.

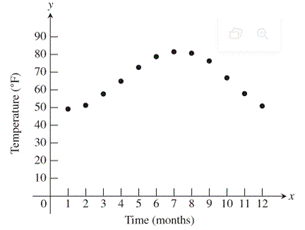
To determine: The fitness of graph as sinusoid in a scatter plot of the data.

The graph is very good fir for the data.

Given Information:

The figure is defined as,

  

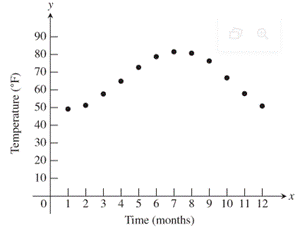
Explanation:

Consider the given information,

Substitute all the obtained values in the previous parts in the given function.

  $y=16.15\sin \left[\frac{\pi }{6}\left(t-4\right)\right]+65.35$

Use the graphing calculator to insert the table in the calculator.

  

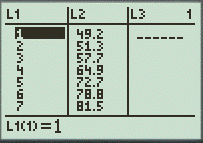
Now, enter the function.

  

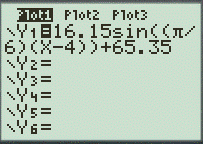
Set the window as per demand of the function and draw the function table in same window.

  

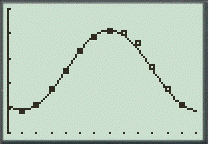
As can be seen from the graph, the sinusoid equation is a very good fit for the data.

Therefore, this is best fit.

e.

To determine: The dates in the year when the mean temperature will be $70°$ .

The obtained values are $t\approx 4.56\to \text{May }17$ and $t\approx 9.44\to \text{October }14$ .

Given Information:

The figure is defined as,

  

Explanation:

Consider the given information,

Graph the horizontal line $y=70$ representing $70°\text{F}$ together with the sinusoid and use the intersect feature to obtain the following t -values.

  

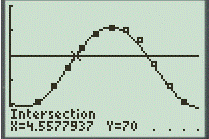
And,

  

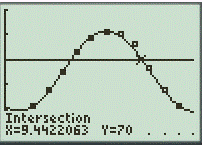
Where, the first value is representing as $t\approx 4.56$ , 4 represents May and $0.56$ represents $0.56\left(31\right)\approx 17$ so the predicted date is May 17. In $t\approx 9.44$ , 9 represents October and $0.44$ represents $0.44\left(31\right)\approx 14$ so the predicted date is October 14.

Therefore, the above values are the required values.