Chapter 4.7, Problem 80E

The blood vascular system consists of blood vessels (arteries, arterioles, capillaries, and veins) that convey blood from the heart to the organs and back to the heart. This system should work so as to minimize the energy expended by the heart in pumping the blood. In particular, this energy is reduced when the resistance of the blood is lowered. One of Poiseuille’s Laws gives the resistance R of the blood as

$R=C\frac{L}{r^4}$

where L is the length of the blood vessel, r is the radius, and C is a positive constant determined by the viscosity of the blood. (Poiseuille established this law experimentally, but it also follows from Equation 8.4.2.) The figure shows a main blood vessel with radius r₁ branching at an angle θ into a smaller vessel with radius r₂.

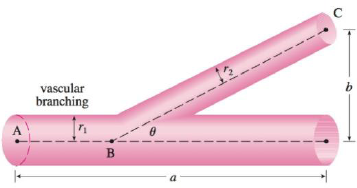
(a) Use Poiseuille’s Law to show that the total resistance of the blood along the path ABC is

$R=C\left(\frac{a-b\cot \theta }{r_1^4}+\frac{b\csc \theta }{r_2^4}\right)$

where a and b are the distances shown in the figure.

(b) Prove that this resistance is minimized when

$\cos \theta =\frac{r_2^4}{r_1^4}$

(c) Find the optimal branching angle (correct to the nearest degree) when the radius of the smaller blood vessel is two-thirds the radius of the larger vessel.