
Concept explainers
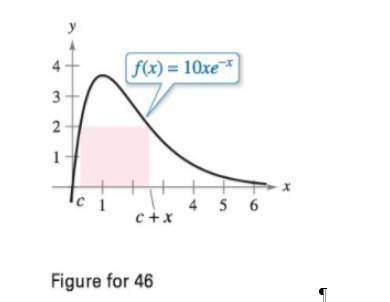
Area Perform the following steps to find the maximum area of the rectangle shown in the figure.
(a) Solve for c in the equation
(b) Use the result in part (a) to write the area A as a function of x. [Hint:
(c) Use a graphing utility to graph the area function. Use the graph to approximate the dimensions of the rectangle of maximum area. Determine the required area.
(d) Use a graphing utility to graph the expression for c found in part (a). Use the graph to approximate
Use this result to describe the changes in the dimensions and position of the rectangle for
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
CALCULUS EARLY TRANSCENDENTAL FUNCTIONS
- How can you use the discriminant when you are graphing a quadratic function?arrow_forwardA path of a toy rocket thrown upward from the ground at a rate of 208 ft/sec is modeled by the quadratic function of. h(x)=16t2+208t. When will the rocket reach its maximum height? What will be the maximum height?arrow_forwardWrite the quadratic function in f(x)=a(xh)2+k form whose graph is shown.arrow_forward
- Solve the following application problem. A rectangular field is to be enclosed by fencing. In addition to the enclosing fence, another fence is to divide the field into two parts, running parallel to two sides. If 1,200 feet of fencing is available, find the maximum area that can be enclosed.arrow_forwardA forest fire leaves behind an area of grass burned in an expanding circular pattern. If the radius of the circle of burning grass is increasing with time according to the formula r(t)=2t+1 , express the area burned as a function of time, t (minutes).arrow_forwardThe rate of change of an autocatalytic chemical reaction is kQxkx2 where Q is the amount of the original substance, x is the amount of substance formed, and k is a constant of proportionality. Factor the expression.arrow_forward
- Given information about the graph of a quadratic function, find its equation. Vertex (2,0) and point on graph (4,12).arrow_forwardA rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to r(t)=25t+2 , find the area of the ripple as a function of time. Find the area of the ripple at t=2 .arrow_forwardYou have 600 yards of fencing to enclose a rectangular field. Express the area of the field, A, as a function of one of its dimensions, x.arrow_forward


 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt





